이번 포스팅에서는 벡터의 선형독립(Linear Independence)와 기저벡터(Basis)에 대해 알아보려고 한다. 선형독립과 기저벡터는 머신러닝의 PCA(주성분분석), SVD(Singular Value Decomposition), LDA(선형판별분석)을 배울 때 연관되어 있는 개념이다.
우선 본격 주제에 들어가기 앞서서 저번 포스팅에서 배웠던 Ax=0라는 Rectangular Matrix의 경우에 영벡터공간(Null Space)과 결부지어서 이제는 영벡터공간이 아닌 연립방정식인 Ax=b의 해집합을 어떻게 나타낼지에 대해서 살펴보자.
먼저 Ax=0이라는 연립방정식의 해집합을 구할 때 다음과 같은 수식으로 구해짐을 우리는 저번 포스팅에서 알게되었다.
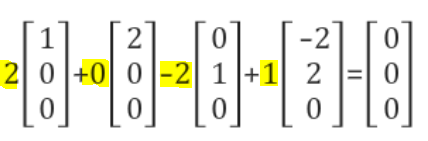
위와 같은 식으로 영벡터공간의 해집합을 구하게 됬는데 이제 영벡터공간이 아닌 Ax=b라는 연립방정식을 가우스 소거법을 이용하고 나오게 되는 식은 밑의 그림과 같다.

즉, A라는 행렬을 Row Reduced form형태의 행렬로 만들어주게 된다. 밑의 그림을 보면서 Ax=b의 해집합을 찾아가는 과정을 살펴보자.

우선 1.Ax=b를 가우스 소거법을 이용해 R형태(Row Reduced Form)형태로 만들어준다. 왜냐하면 해집합이 존재하도록 하기 위함 때문이다. 그리고 2.Free/Pivot variable을 구분해주고 Linear Combination의 Scala값엔 Free variable을 넣어주고 끝에 d에 해당하는 벡터는 Pivot variable의 계수만 살아있도록 해준다.(즉, Free variable에 해당하는 계수들은 0으로 만든다.) 3.마지막으로는 영벡터공간에서 처럼 Linear Combination 형태로 만들어 준다.
1. Linear Independence (선형 독립)
이제 본격적으로 선형독립에 대한 내용이다. 선형 독립이란, 임의의 다른 Scala값(C값)을 각 벡터 V1~Vn앞에 곱해준 값들의 벡터들을 모두 더했을 때 0이 되는 것이다. 이 때 0값이 되기 위해서는 반드시 Scala값들이 모두 0이어야 한다. 이 때 우리는 벡터들이 서로 '선형 독립'이라고 하게 된다.

그렇기 때문에 가우스 소거법을 이용하고 난 후 만약 모든 행렬의 모든 행까지 Upper Triangle형태로 나오게 된다면 모든 Column Vector들이 서로 선형독립이라는 의미이다. 하지만 그렇지 않을 때 하나의 요소라도 0이 아닌 즉, non-zero값이 들어 있는 행의 개수는 결국 선형 독립인 Column Vector들의 개수를 의미한다.
다음은 행렬의 Rank에 대한 개념이다. Rank는 여러가지 의미를 지니고 있다.
- 선형독립인 Column 벡터들의 개수
- 선형독립인 Row 벡터들의 개수
- 가우스 소거법을 취했을 때 Pivot들의 개수
- 벡터 공간의 차원(Dimension)
따라서 만약 가우스소거법을 취한 후 행렬의 non-zero값들인 행의 개수가 5개이거나 Pivot값들의 개수가 5개라면 그 때 Rank는 5가 된다.

다음은 Span 이라는 개념이다. Span을 한국어로 정의한다면 V1~Vn이라는 벡터들의 모든 선형결합 조합들이 하나의 특정한 Vector Space를 구성한다면 V1~Vn이라는 벡터들은 해당 Vector Space를 'Span'한다라고 할 수 있다.
위 그림의 밑의 ex)를 보게되면 각각 2개와 3개의 Column Vector들로 x,y 2차원 평면을 구성할 수 있다. 이 때 물론 3개의 Column vector의 경우에는 3개 중 하나가 불필요할 수도 있다.
이때 이 2가지 경우(Column vector가 2개일 경우와 3개일 경우)에서 차이점은 Span방법이 다르다는 것이다. 즉, 2개의 Column Vector로 2차원 평면을 Span할 때에는 2개의 Column vector들의 선형결합이 unique하지만 3개의 Column Vector로 2차원 평면을 Span할 경우에는 선형결합이 unique하지 않고 여러개가 존재한다는 것이다.
그렇다면 이러한 선형결합이 unique한지 아닌지를 어떤 것으로 판단할까? 바로 이 때 Basis(기저벡터)의 개념이 등장하게 된다.
2. Basis(기저 벡터)
우선 기저벡터란, 특정한 Vector Space를 Span(구성)해주는 선형 결합 벡터들의 최소 개수이다. 위의 예시를 들면 2개 Column vector일 때의 경우에는 Basis라고 할 수 있지만 3개의 Column vector일 경우에는 Basis라고 할 수 없는 것이다.
따라서 기저벡터는 특정 벡터공간을 만들 때 벡터들의 선형 결합이 Unique하다고 할 수 있다.

하지만 기저벡터 자체는 Vector Space를 구성하는 데에 있어서 Unique하지 않다. 위 그림의 예시나 아까 x,y 2차원 평면을 만들 때의 예시만 들어보아도 알 수가 있다. 즉, 2차원 평면을 구성하는 데 있어서 최소 선형독립 벡터의 개수는 [1,0]과 [0,1] 이 있을 수 있고 또 [1,0], [1,1] 이 있을 수 있기 때문이다. (단, [1,0] 은 행 벡터가 아닌 '열 벡터' 이다.)
이제 점차 Unique해야 함에 있어서 Basis와 Linear Combination이 헷갈릴 수 있는데 다음과 같이 정리하고 넘어가자.
- 특정 벡터공간을 구성(span)하는 선형독립 벡터들의 최소 개수인 Basis은 여러개이다.(not unique)
- 하지만 특정한 Basis안에서의 벡터들의 Linear Combination의 Scala값은 Unique하다!(즉, 선형결합이 Unique하다.)
참고로 만약 Linear Combination을 이루는 벡터들이 서로 수직관계라면 선형결합에 붙는 Scala값을 쉽게 구할 수 있고 이는 결국 Rectangular 연립방정식의 최종적인 해집합을 구할 수 있다.
'Data Science > 선형대수' 카테고리의 다른 글
| 벡터공간의 4가지 부벡터공간(Subspaces) (0) | 2020.06.07 |
|---|---|
| 영벡터공간(Null Space)과 해집합 (0) | 2020.05.19 |
| 벡터공간(Vector space)과 열벡터공간 (0) | 2020.05.18 |
| Inverse Matrix(역행렬)&Transpose Matrix(전치행렬) (0) | 2020.05.17 |
| LU Decomposition(LU 분할) (0) | 2020.04.28 |



