※해당 게시물에 사용된 일부 자료는 순천향대학교 빅데이터공학과 정영섭 교수님의 머신러닝 전공수업 자료에 기반하였음을 알려드립니다.
이번 포스팅에서는 Bayes Rule에 기반으로 하는 머신러닝 모델인 Bayesian Networks에 대해 알아보려고 한다. 그 전에 먼저 Bayesian Networks는 Bayes Classifier의 일반화 버전이다. 어찌됬든 두 개가 다른 모델이지만 Bayes에 관련된 머신러닝 모델들 여러가지를 포함하는 용어가 Bayesian Networks이다.
본격적인 머신러닝 모델들을 배우기 전에 가장 기반이 되는 Bayes Rule(베이즈 정리)를 알아보고 가자. 앞으로 전개해나갈 내용에 대한 목차는 다음과 같다.
1. Bayes Rule(베이즈 정리) 개념
2. Bayes Classifier 개념과 한계
3. Naive Bayes Classfier 개념과 한계
4. Gaussian Naive Bayes Classifier(GNB) 개념과 한계
5. Bayesian Networks(베이즈 네트워크)
1. Bayes Rule(베이즈 정리) 개념
지난 확률과 통계 시간에서도 배웠던 베이즈 정리에 대한 개념이다. 베이즈 정리는 우리가 구하고 싶은 확률을 Observation data(이미 알고있는 데이터)에 기반하여 조건부확률과 Total Probability를 이용해서 구하는 공식을 말한다. 말로 하면 이해가 잘 안되니 밑의 그림을 보면서 이해해보자.

베이즈 정리 식의 각 요소에 대해 알아보기 전에 H, e 에 대해서 정의해보자. 여기서 H란, 가설(Hypothesis)이며 우리가 만들려고하는 머신러닝 모델이라고 생각하면 된다. 반면에 e는 evidence이며 '사건' 즉, 우리가 이미 관찰한 Observation Data를 말한다. 이제 각 요소를 알아보자.
- Posterior : 우리가 본질적으로 구하고자 하는 것이며 직접 계산을 할 수 없기 때문에 다른 요소들(Likelihood, Prior, Marginal)을 이용해 계산한다.
- Likelihood : 고등학교 시절 배웠던 '조건부확률' 이다.
- Prior : 아무 조건없이 단순히 '가설'이 발생할 확률이다.
- Marginal : 이 요소를 구하기 위해서 우리는 Total Probability를 이용한다.
Bayes Rule을 계산하는 방법에 여러가지 다양한 문제들은 해당 링크를 참고해서 이해해보자.
https://www.synapsoft.co.kr/blog/6002
조건부 확률(베이지안)의 이해를 위한 예제 및 풀이 - 사이냅소프트
조건부 확률(베이지안)의 이해를 위한 예제 및 풀이 v1.0 2007/10/11 Copyleft by 전경헌@사이냅소프트 v1.1 2007/10/16 Copyleft by 전경헌@사이냅소프트 , 몬티홀 문제에 대한 커멘트 추가 v1.2 2011/03/17 Copyleft by 전경헌@사이냅소프트 , 몬티홀 문제를 별도 블로그로 기록함 베이스의 정리(Bayes’ theorem)는 공부할 때마다 새로운 느낌이 든다. 매번 아하 그렇지 라는 생각이 들다가도 좀
www.synapsoft.co.kr
2. Bayes Classifier 개념과 한계
이제부터 소개할 개념들에 대해서는 장황한 말보다는 수업자료와 설명을 함께 이용하여 소개하려고 한다. 먼저 다음과 같은 문제를 보자.

위와 같이 4마리의 물고기(Fish1 ~ Fish4)의 학습데이터가 있다고 하자. 그리고 물고기의 Class(Label)는 Salmon과 Sea bass 두 개이다. 그리고 다음과 같이 정의해줄 수 있다.
- 이 때 새로운 물고기(새로운 데이터)가 10cm라는 Feature가 확인이 되었다. => e(evidence)
- 이 물고기는 Salmon인가 Sea bass인가? 하는 문제를 풀어보자. => H(Hypothesis)
우리가 구하고자 하는 식 두 가지는 다음과 같다. (이 때, x=10cm)
- P(Salmon | 10cm) : evidence가 10cm일 때 Salmon일 확률(H)은?
- P(Sea bass | 10cm) : evidence가 10cm일 때 Sea bass일 확률(H)은?
우리는 위와 같은 두 개의 Posterior 식을 베이즈 정리를 통해서 구해줄 수 있다. 그리고 두 개의 Posterior 식 중 확률이 더 높은 것을 최종 Class로 채택하는 것이다.
그렇다면 이 Bayes Classifier의 한계점은 무엇일까? 다음 그림을 보자.

이번에는 학습데이터에 Fish들의 무게(kg)라는 Feature가 추가되어 학습되었다. 이 때 새로운 물고기가 10cm이고 무게가 10kg일 때, Salmon일까? Sea bass일까?(어떤 것이 evidence고 Hypothesis라고 나타내는 과정은 생략하겠다. 이전에 했던 예시랑 똑같이 적용해주면 된다.)
이전의 예시와 마찬가지로 P(Salmon|10cm, 10kg) , P(Sea Bass|10cm, 10kg) 일 때 두개의 확률을 베이즈 정리를 통해서 구해보자. 그런데 문제가 생겼다. 바로 새롭게 주어진 데이터의 Feature(10cm, 10kg)가 기존에 학습되어진 데이터(Fish1 ~ Fish4)에 존재하지 않기 때문에 확률이 0이 되버리는 것이다.
우리는 이러한 문제를 해결하기 위해서 '빈도수'에 기반하여 계산을 하는 Naive Bayes Classifier을 이용할 것이다.
3. Naive Bayes Classifier 개념과 한계
이번 개념도 위와 같은 물고기 예시를 들면서 살펴보자.

우선적으로 Naive Bayes Classifier가 가정(Assume)하는 개념이 한 가지가 있다. 바로 Feature들이 서로 독립적이라는 것을 가정한다. 확률과 통계 시간에서 배웠던 것처럼 '독립'이라는 것은 정말 강력한 특성임을 알 수 있었다.
그래서 독립사건이면 P(A, B) = P(A)P(B) 인 공식을 이용하여 레몬색 형광펜으로 칠해진 likelihood 확률식을 잘 풀어주고 우리가 구하고자 하는 Posterior 확률을 구할 수가 있다.
이 Naive Bayes Classifier도 마찬가지로 두 개의 Posterior 확률 중 더 큰 값을 최종 Class로 채택을 하게 된다.
또 그렇다면 이 Naive Bayes Classifier의 한계점은 무엇일까? 다음 그림을 보자.

이번에 새로 주어진 데이터의 Feature 종류의 각 값이 기존에 학습되어진 데이터의 Feature들 값에 존재하지 않는다면 어떻게 될까? 즉, 위 그림에서는 새로운 Feature 종류의 각 값이 17cm, 20kg이다. 이러한 값들이 학습 데이터에 있었던 Feature의 값들에 존재했던 적이 없다는 것이다.
우리는 이러한 문제를 해결하기 위해서 Gaussian Naive Bayes Classifier를 활용할 수 있다.
4. Gaussian Naive Bayes Classifier(GNB) 개념과 한계
GNB는 기존의 Naive Bayes모델과 달리 '빈도수'에만 기반하여 계산하는 것이 아닌 특정 분포, 그 중에서도 가우시안(정규) 분포를 따른다고 가정하는 것이다. 정규분포의 식과 GNB의 식은 각각 다음과 같다.

우선 식에서 특정 변수가 나타내는 의미를 알고 넘어가야 다음에 연이어 소개할 식들의 해석이 쉬울 것이다.
- i : 몇 번째 Feature인지 나타내는지를 의미
- k : 몇 번째 Label인지 나타내는지를 의미
그리고 Y끼리 또는 Xi끼리 또는 Xi, Y끼리 둘 다 서로 독립적이라고 한다면 Parameter를 줄여줄 수 있다.
다음은 이제 GNB로 데이터를 학습하고 테스트해보는 과정을 살펴보자.

우선, 학습하는 과정부터 살펴보자. 본문 속 내용을 살펴보면
πk는 P(Y= yk) 라고 정의되고 있다. 이는 πk는 k번 째 Label일 확률임을 의미한다. 그리고 Xi 라는 i번째 Feature은
μ ik 라는 평균값과, σ ik 라는 표준편차를 취하게 된다.
다음은 밑의 테스트하는 과정이다. 그림 속 수식이 좀 복잡한데, Xnew 라는 것은 New Feature값의 데이터이며 해당 GNB모델을 통해 Ynew 값의 Label를 분류해주는 것이다. 해당 식이 일반화되어 있기 때문에 이해하는 데 어려움이 있어 필자가 직접 밑에 검은색 볼펜으로 필기를 한 Fish 예시를 통해 단계적으로 이해해보자.
<1단계>
1) Xnew 의 Feature가 19cm, 9kg 이라는 New 데이터가 주어졌다고 하자. 우리는 이를 통해 Yk값이 Salmon인지 Sea bass인지 분류해주어야 한다.
<2단계>
2) ΠP(Xi | Y= yk) 이 수식은 i,k에 해당하는 모든 확률을 곱(Product)하라는 뜻인데 해당 예시에 적용해보면 다음과 같아진다.
- Salmon으로 분류할 경우 : P(19cm | Salmon) x P(9kg | Salmon)
- Sea bass으로 분류할 경우 : P(19cm | Sea bass) x P(9kg | Sea bass)
<3단계>
위에서 정의해준 확률들은 모두 Posterior 확률이다. 첫 번째에서 배웠던 Bayes Rule을 이용하여 확률을 구해준 후 arg max(가장 높은 확률을 채택)로 최종 class을 채택해준다.
만약 그렇다면 GNB의 테스트 시에, Y의 Label이 n개라고 할 때, 측정(estimate)해야 할 Posterior 확률 갯수는 몇개를 하면 될까? 답은 n-1 이다. 왜냐하면 모든 확률의 합은 결국 1이기 때문이다.
그리고 이러한 Posterior 구하는 확률을 계산하는 방식을 정규분포(Gaussian 분포)로 바꾸어준 것이 제일 하단의 식이다.
Xi라는 새로운 Feature는 μ ik 라는 평균값과, σ ik라는 분산값을 따른다는 것인데 이를 어떻게 계산하면 평균과 분산값이 나오지는지는 아래그림을 보자.

계산 방법은 이른바 MLE(Maximum Likelihood Estimates)를 이용하는데 수식에 대한 설명은 위 그림 속 필기된 내용과 같다.
#MLE에 대해 궁금하다면 ? https://techblog-history-younghunjo1.tistory.com/70
5. Bayesian Networks(베이즈 네트워크)
베이즈 네트워크는 기본적으로 이전의 모델들이 해결하지 못했던 XOR문제를 해결할 수 있다. 베이즈 네트워크는 Belief 네트워크 또는 Casual 네트워크라고도 불린다. 다음 필기를 보면서 6가지 규칙을 기억하자!
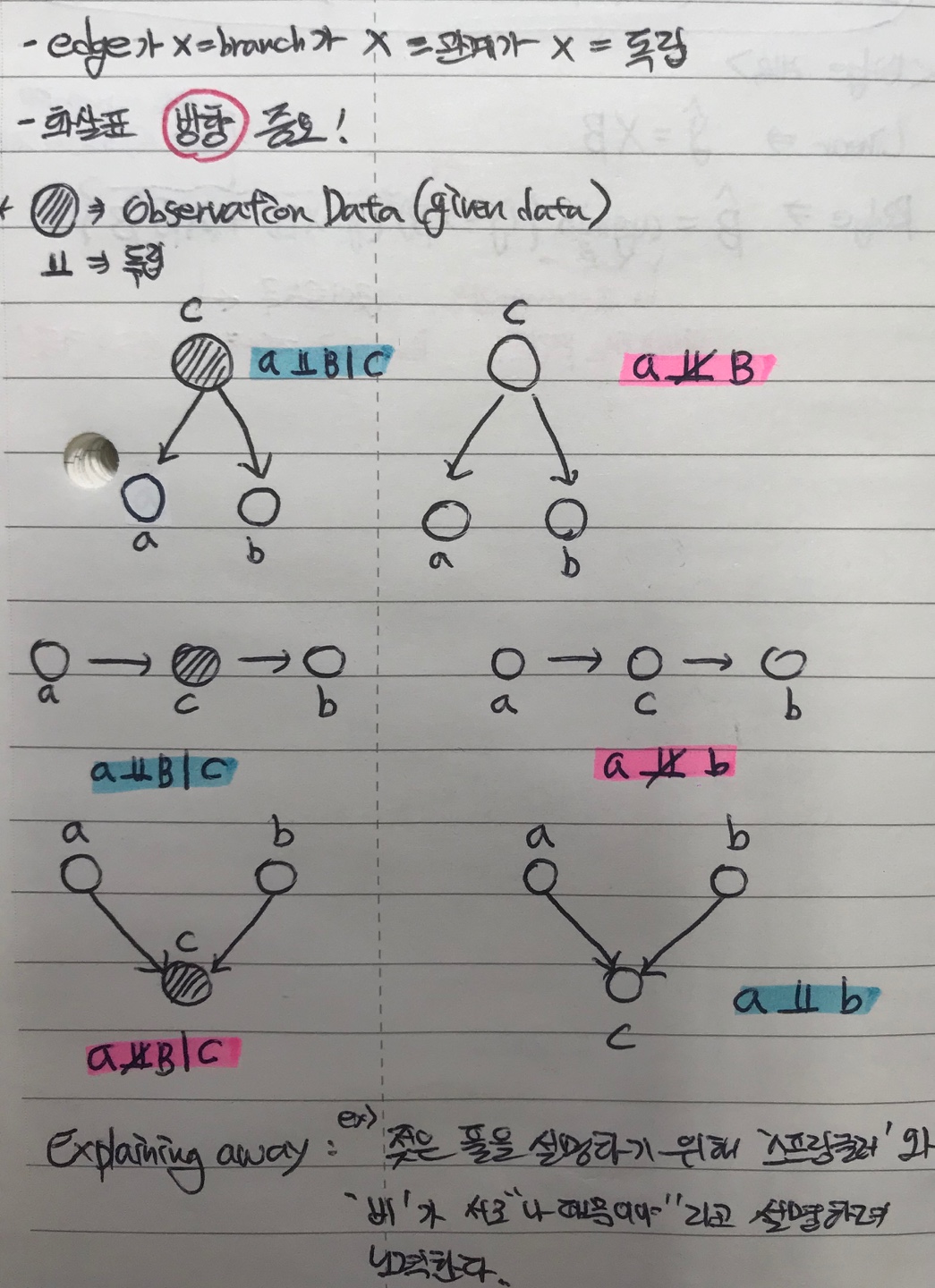
사진 이외로 추가적으로 설명할 부분은 Explaining away 라는 개념이다. 일반화된 정의를 설명하면 이해를 못하기에 직관적으로 예시를 들어 설명하려고 한다. 예를 들어 젖은 풀이라는 결과를 설명하기 위해서 '스프링쿨러' 와 '비(rain)'가 서로 젖은 풀을 설명하고 노력하는 것이다. 다시 말해, '스프링쿨러'는 "나 때문에 풀이 젖었어!" 라고 말하고 '비(rain)'도 "아니야 나 때문에 풀이 젖은거야" 라고 말하면서 서로 '젖은 풀'이 나 때문이라고 주장하는 것이다.
5-1. 분류를 위한 Bayesian Networks
우리가 위에서 소개했던 Bayesian Networks를 이용해서 분류(Classification) 문제를 해결할 수 있다.
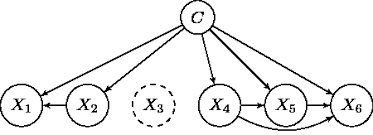
위와 같이 Class C와 각 Feature(X1 ~ X6)간의 edge를 설정하고 베이즈 네트워크의 각 노드들의 확률을 완성한다. 이 때는 Frequency에 기반한다. 그리고 베이즈 네트워크를 이용해 Posterior 확률(우리가 해결하고자 하는 문제)를 계산 후 가장 큰 확률값의 Label을 채택하게 된다.
그렇다면 Naive Bayes Classifier과 Bayes Networks와의 관계는 어떠할까? 그림을 통해서 차이점을 이해해보자.
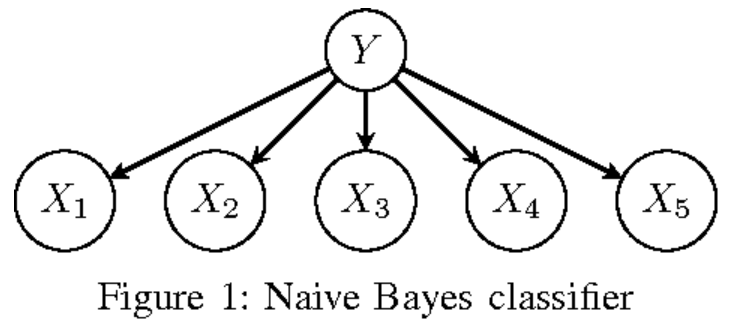
베이즈 네트워크의 그림과 차이점이 명확히 보이는가? 베이즈 네트워크와 달리 Naive Bayes Classifier은 Feature들(X1~X5)들끼리 서로 '독립'임을 가정하는 것이다.
마지막으로 번외목차로 Classification의 종류에 대해서 알아보고 차이점에 대해서 짚고 넘어가려고 한다.
- Binary Classification : 우리가 위에서 물고기 예시를 들었던 것처럼 분류할 Label이 2개일 때를 말한다.
- Multi-class Classification : 각각의 데이터는 1개의 Class(Label)만 가질 수 있다.
- Multi-label Classification : 동시에 여러개의 Class에 대한 Label들을 가질 수 있다.
이 때 Multi-label Classification에 대해서 헷갈릴 수 있는데 간단한 예시를 들어서 살펴보자. Class가 {'모자', '선글라스', '스카프'} 이렇게 총 3가지가 있다고 가정하자. 이 때 하나의 데이터는 앞서서 정의했던 Class의 3개들 중 특정 1개만 label로 선택할 수 있는 것이 아닌 여러개 즉, {'모자', '선글라스'} 2개를 선택할 수도 {'모자', '스카프' 또는 '모자'}, {'선글라스', '스카프'} 이렇게 모두 선택할 수가 있다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] PCA(주성분분석), SVD, LDA by Fisher (0) | 2020.04.25 |
|---|---|
| [ML] Linear Regression(선형회귀)& Logistic Regression (0) | 2020.04.24 |
| [ML] Decision Tree(의사결정나무) (0) | 2020.04.10 |
| [ML] 머신러닝의 종류와 용어개념 (0) | 2020.04.05 |
| [딥러닝] NN(Neural Network)의 등장과 개념 (0) | 2020.03.14 |



