※해당 게시물에 사용된 일부 자료는 순천향대학교 빅데이터공학과 정영섭 교수님의 머신러닝 전공수업 자료에 기반하였음을 알려드립니다.
이번 포스팅에서 머신러닝 모델 종류 중 가장 쉽고 단순한 Decision Tree(의사결정나무) 모델에 대해서 알아보려고 한다. 앞으로 전개할 컨텐츠 순서는 다음과 같다.
1. Decision Tree의 전체적인 구조
2. 좋은 Tree 란?
3. Decision Tree 생성 알고리즘인 'ID3 알고리즘'
4. Tree 생성 순서
5. Decision Tree의 기타 특징
1. Decision Tree의 전체적인 구조
의사결정나무의 전체적인 구조는 우리가 지금껏 살아오면서 쉽게 접했을 수 있는 모형이다. 다음 그림을 보면서 Tree를 구성하고 있는 여러 부분들의 용어를 알아보자.

위 그림을 보면서 하나 하나 세부적인 구성요소들의 용어를 익혀보자.
- Root node : 그림 속 "Work to do?"의 부분으로 Decision Tree가 시작되는 node를 말한다.
- Branch : edge라고도 하며 node에서 node로 가는 길목이라고 생각하면 된다.
- Internal node : Decision node라고도 부르며 하나의 branch로 가기 위해 '결정'을 해주는 node라고 생각하면 된다.
- Leaf node : External node 또는 Terminal node라고도 하며 분류문제에서 class(label)에 해당하는 node 이다.
- 단, 우리가 이전 포스팅에서 언급했던 Feature(Attribute)라고 할 수 있는 부분은 Decision Tree 모형에서 Internal node라고 할 수 있다.
- 참고로 더이상 Feature(Internal node)가 없으면 leaf node로 간주하고 자식 노드를 생성하지 않는다. 또한 Leaf node가 더이상 없다면 가장 많은 수의 label이 있는 것을 결과로 채택한다.
2. 좋은 트리란?
그렇다면 어떤 트리가 좋은 트리라고 할 수 있을까? 그걸 알아보기에 앞서 보통 '트리의 높이(깊이)' 를 결정하는 요소는 Internal node의 개수에 영향을 받는다. 즉, Internal node 개수가 증가할 수록 트리는 높아진다(깊어진다).
이제 좋은 트리의 조건을 알아보자. 생각해보면 간단하다.
"Leaf node의 한 쪽에 통일된 label 데이터들만 남으면서 트리의 높이가 짧은 트리!"
이러한 좋은 트리 조건을 충족시키기 위해서는 Feature의 선정 순서(Internal node 순서)가 중요하다. 적절한 Feature 순서를 선정하는 기준은 데이터를 가장 잘 나누어줄 수 있는 Feature를 선정하는 것이다. 그렇다면 데이터를 가장 잘 나누어줄 수 있는 기준은 어떻게 설정할 것인가? 그것은 수학적으로 계산해 설정해주어야 한다.
3. Decision Tree 생성 알고리즘인 'ID3 알고리즘'
위에서 '수학적으로 계산'을 하기 위해 사용하는 알고리즘이 바로 'ID3 알고리즘' 이다. 이러한 알고리즘을 이해하기 위해서는 기본적으로 몇 가지 개념을 이해해야 한다. 우선 그림을 보면서 직관적으로 이해해보자.

- Purity : 한 쪽 데이터만 존재할 수록 more purity라고 할 수 있다. 위 그림 속에서는 맨 오른쪽의 경우가 the best purity라고 할 수 있다.
- Entropy : Purity의 반대 개념이다. Impurity라고도 하며 클수록 Chaotic(혼란스러움)하다. 따라서 Entropy가 클수록 정보(Information)이 많음을 의미한다. Entropy를 구하는 수식은 다음과 같다.

- Information Gain(정보획득) : 이 개념을 소개하기 전에 우리는 한 가지 생각을 해볼 수가 있다. "자식 node들이 갖는 데이터가 pure할수록 좋잖아! 그렇다면 부모노드의 Purity와 여러 자식 노드들의 Purity를 비교해서 차이가 가장 클수록 좋은 Feature가 아닐까?" 라고 말이다. 따라서 우리는 정보획득의 공식을 다음과 같이 정의할 수 있다.
Informatin Gain(정보획득) = (부모노드의 Entropy) - (자식노드의 Entropy)
이 때, 정보획득의 값은 0~1 사이이며, 자식노드가 2개 이상이라면 정보획득을 구하는 공식의 '자식노드의 Entropy'는 '자식노드들의 Entropy 평균값'으로 대체한다.
따라서 우리는 IG가 큰 Feature를 선택하며 이것은 곧 데이터를 가장 잘 나누어주는 Feature라고 할 수 있을 것이다.
하지만 명심해야 할 점은 IG가 가장 큰 Feature가 가장 좋은 트리를 100%보장하는 것은 아니라는 것이다.
IG를 구하는 구체적인 예시는 밑의 그림을 보면서 이해해보자.

4. Tree 생성순서
이제 좋은 트리를 만들기 위한 조건도 알아보았고 어떻게 만드는지 방법에 대해서도 알아보았다. 그러면 지금까지 순차적으로 배웠던 내용을 종합하여 Tree 생성순서를 단계적으로 알아보자.
#노드 순서는 Root에서 Leaf 노드로 간다.
- 노드에서 고려할 데이터가 이미 하나의 class에 속하거나 더 이상 feature가 없어서 leaf node가 된 경우, 가장 많은 수의 class를 결과값으로 채택
- 각 노드에서 고려할 feature 생성시, IG가 가장 큰 feature를 선택(단, Leaf node에서 완벽하게 나누어진다는 보장은 없다!) #참고로 IG가 가장 큰 Feature라고 해서 가장 높은 성능을 보장하진 않는다는 것을 기억하자.
- 선택된 feature에 대한 조건별로 '자식 노드' 생성
- 각 자식 노드에서 해당 조건을 만족하는 데이터끼리 1번부터 반복
따라서 다음과 같이 한 문장으로 요약해보자면 "처음에 feature별로 IG를 계산 후 가장 높은 feature를 선정. 그리고 처음에 선정한 feature을 제외하고 다음으로 IG가 높은 feature를 선정......" 이런 식으로 프로세스가 진행된다고 보면 된다.
5. Decision Tree의 기타 특징
5-1. Real-value feature(회귀분석)에서는 Terminal node의 예측값의 평균값을 반환한다. 그리고 Value bin Tree를 만드는데 Value bin Tree는 다음과 같다.
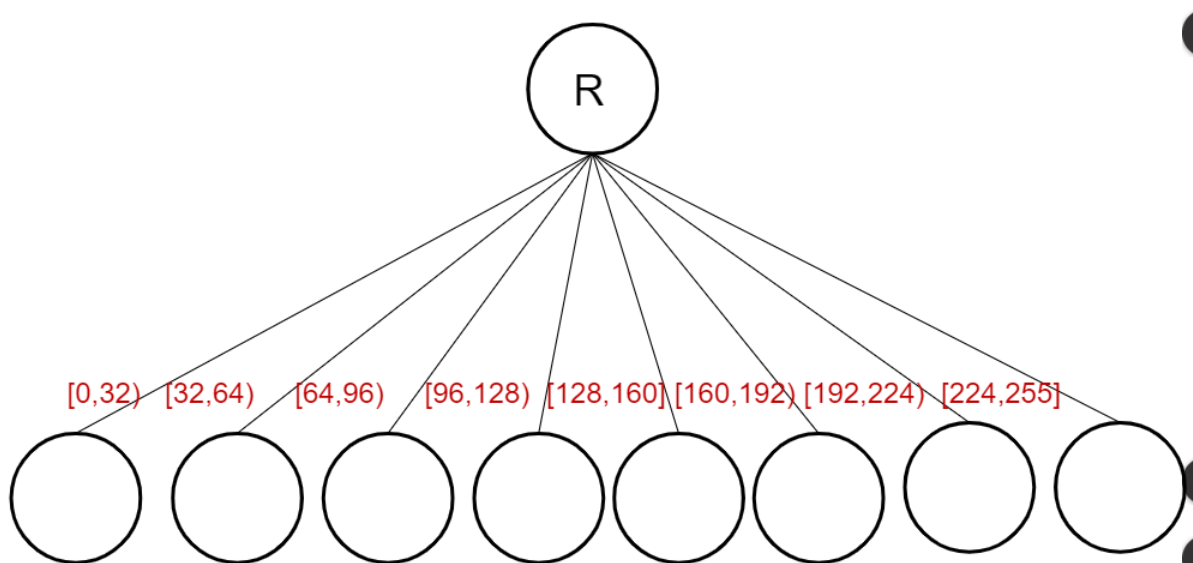
그림속 R은 Root node이며 빨간색으로 적혀있는 부분의 설명은 다음과 같다. 첫 번째에 [0,32) 라고 적혀 있는데 이는 0이상 32미만을 뜻한다. 이렇게 "[" = 이상, ")" = 미만 이라고 생각하며 빨간색 글씨를 똑같은 방식으로 해석하면 된다. 만약 주어진 Data의 값이 76이라는 Real-value라면 [64, 96) node에 들어가게 되는 것이다.
5-2. Decision Tree는 Overfitting이 되기 쉬울까?
결론부터 말하자면 되기 쉽다. 왜냐하면 하나의 node에서는 해당 node만 생각하기 때문에 만약 하나의 error 데이터가 발생한다면 '나비효과' 처럼 다른 node들에게도 심각한 영향을 주기 때문이다.
5-3. Decision Tree는 Feature를 Normalize 할 필요가 있을까?
답은 "할 필요가 없다" 이다. 만약 키가 170cm 이상이면 남성, 170미만이면 여성, 이라고 Internal node를 만들었을 때 이를 0,1로 각각 normalize한다고 해도 어떤 효과가 발휘할까? 결론적으로 똑같이 나눌 뿐이다.
5-6. Decision Tree의 모양에 따른 용어
아까 언급했던 것처럼 Internal node에 따라 Decision Tree의 깊이(높이)가 달라진다. 하지만 어떻게 Internal node가 뻗어나가는지에 따라 용어가 달라진다. 다음 그림을 보자.

아마 그림을 보고 직관적으로 이해할 수 있을 것이다. 여기서 Bushy란 영어의미로 '덥수룩 한'이라는 뜻인데, 아마 덥수룩하게 즉, 지저분하게 트리가 뻗어나가 있는 모양에 착안하여 이름을 지은 것 같다.
5-7. Decision Tree의 장,단점
이제 마지막이다. 우리가 지금까지 쭉 알아보았던 Decision Tree의 구조, 알고리즘, 여러가지 특징을 보고 Decision Tree의 장,단점을 알아보고 마무리하자.
- 장점 : 사람이 직접 보고 이해하기 직관적(Intuitive)이다.
- 단점 : 복잡한 문제에 직면하면 모델의 성능이 쉽게 저하된다.
이렇게 Decision Tree에 대해서 깊으면서도 얕은(?) 하지만 어려웠던 내용들을 모두 다루어 보았다. 다음 포스팅에서는 내가 블로그의 확률 및 통계 포스팅에서 다루었었던 'Bayes Rule(베이즈 정리)'를 기반으로 하는 Bayesian Networks에 대해 다루어 볼 예정이다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] Linear Regression(선형회귀)& Logistic Regression (0) | 2020.04.24 |
|---|---|
| [ML] Bayesian Networks(베이즈 네트워크) (2) | 2020.04.13 |
| [ML] 머신러닝의 종류와 용어개념 (0) | 2020.04.05 |
| [딥러닝] NN(Neural Network)의 등장과 개념 (0) | 2020.03.14 |
| [ML] 머신러닝 모델링 시 필요한 데이터 종류 그리고 Epoch란? (0) | 2020.03.12 |



