🔊 이번 포스팅에는 최근에 Python으로 알고리즘을 공부하기 시작하면서 알게 된 여러 알고리즘의 원리와 Python으로 구현하는 방법에 대해 소개해보려 한다. 필자는 최근 알고리즘 공부를 '나동빈'님의 '이것이 취업을 위한 코딩 테스트다 with 파이썬'이라는 책과 백준 온라인 저지 사이트로 하고 있다. 이 중 '나동빈'님이 저자이신 책에서 가르쳐주는 내용을 기반으로 배운 내용을 정리해보려 한다.
이번 포스팅에서는 노드들 간의 선후 관계를 고려하여 정렬을 수행하는 정렬 알고리즘 중 하나인 위상(Topology) 정렬에 대해 알아본다. 그리고 이를 구현한 Python 소스코드도 살펴보자.

1. 진입차수
위상 정렬은 정렬 알고리즘이기도 하지만 노드들 간의 선후 관계를 고려한다는 측면에서 그래프 데이터가 주어졌을 때 사용할 수 있는 그래프 알고리즘으로도 분류될 수 있다. 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 다시 말해, 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 방법이다.
위상 정렬을 이해하기 위해서는 진입차수라는 개념을 알아야 한다. 먼저 위상 정렬을 실제 세계의 비유를 통해 이해해보자. 대표적인 예시로는 선수과목을 고려한 학습 순서 설정을 예로 들 수 있다. 예를 들어, 머신러닝이라는 과목을 듣기 위해서는 선형대수를 선수과목으로 들어야 한다. 또 머신러닝을 들으면 딥러닝을 들을 수 있지만 선형대수만 들어도 딥러닝 과목을 수강할 수 있다.(단적인 예시일 뿐 입니다!) 이 과정을 도식화해보면 다음과 같다.

이 때, 진입차수란, 자기 자신으로 연결되어 들어오는 간선의 개수를 의미한다. 예를 들어, 선형대수의 진입차수는 0이다. 머신러닝의 진입차수는 1이다, 딥러닝의 진입차수는 2가 된다.
2. 위상 정렬
위상 정렬은 1번 목차에서 배운 진입 차수와 자료구조 큐를 활용한다. 위상 정렬 알고리즘은 다음과 같은 단계들로 진행된다.
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐에서 노드(원소)를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드(들)을 큐에 넣는다.
- 1번~3번 과정을 큐가 빌 때까지 반복한다.
단, 위 과정을 거치는 동안 모든 원소를 방문하기 전에 큐가 비게 된다면 노드들 간의 사이클이 존재한다는 것이다. 즉, 큐에서 원소가 노드개수($V$)만큼 추출되기 전에 큐가 비어버리면 사이클이 발생한 것이다. 이유는 간단하다. 사이클이 존재하게 되면 진입차수가 0이 될 수가 없기 때문에 어떠한 원소도 큐에 들어갈 수가 없고 사이클이 존재하는 노드들 때문에 꼼짝 못하기 때문이다. 다시 말해 사이클이 판별된 순간부터 큐에 노드는 들어가지 않는다. 기본적으로는 코딩 테스트 문제에서 위상 정렬 문제 카테고리에서는 사이클이 발생하지 않는다고 명시하는 것이 보통이라고 한다.(하지만 책 속 실전 문제에서 사이클이 존재하는 경우의 위상 정렬 문제도 실어놓았다고 해서 풀어볼 예정이다.)
3. 위상 정렬의 동작과정
이제 위상 정렬 알고리즘의 동작과정을 도식화해서 단계별로 살펴보자. 우선 아래와 같은 그래프 데이터가 주어졌다고 가정하자.

3-1. 초기단계
초기 단계에서는 진입차수가 0인 노드를 선형적으로 탐색해서 큐에 넣는다. 현재 노드 1의 진입차수가 0이기 때문에 큐에 노드 1만 삽입한다.

3-2. 두번째 단계
큐에 있는 노드 1을 빼낸다. 그리고 노드 1과 연결되어 있는 간선을 확인한다. 2번과 5번 노드가 존재한다. 이 간선을 모두 제거한다. 그렇게 되면 진입차수가 적혀있는 테이블은 아래와 같이 업데이트 된다. 그리고 진입차수가 0이 된 2번, 5번 노드를 큐에 집어넣는다.
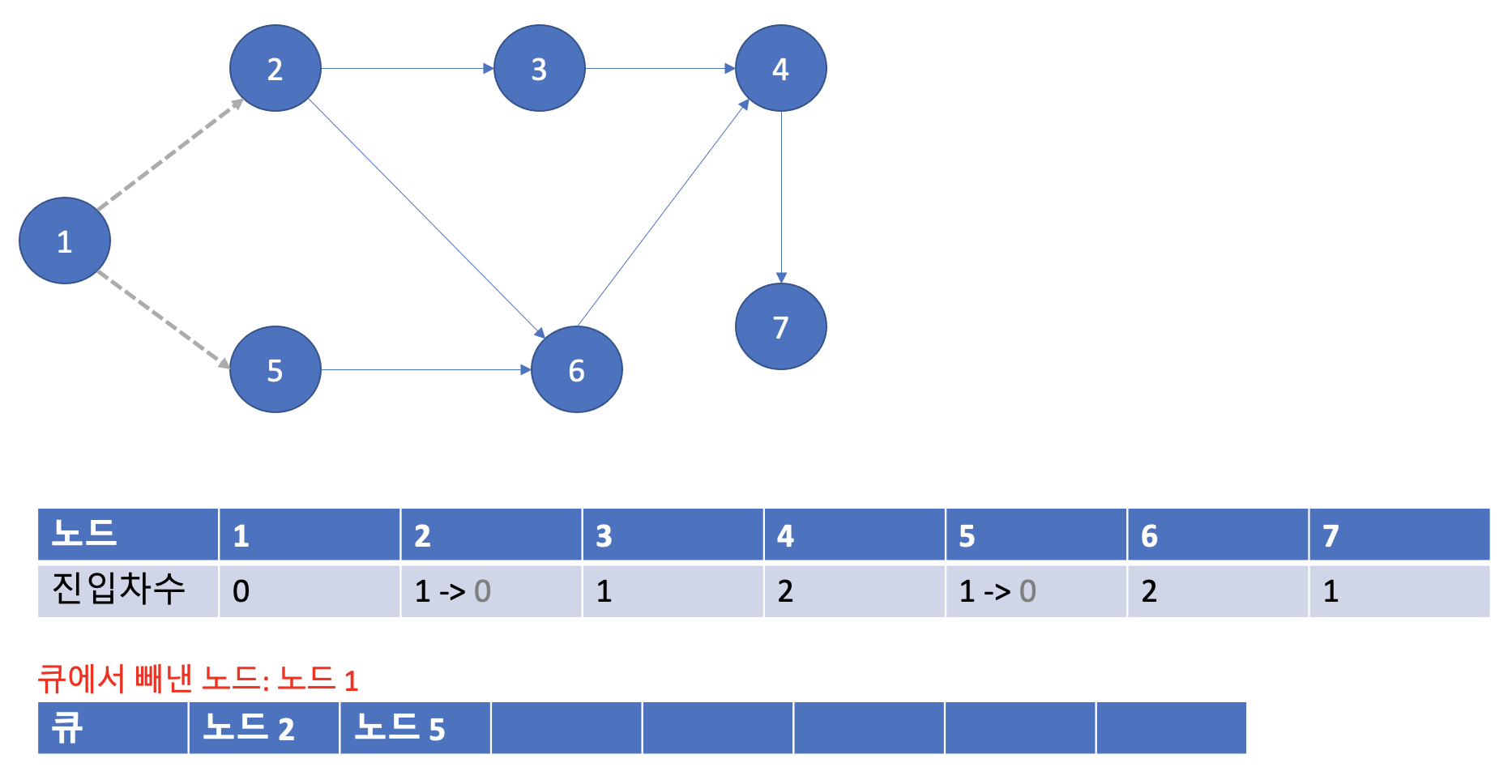
3-3. 세번째 단계
다음에는 큐에 가장 앞에있는 노드 2를 빼낸다. 노드 2와 연결되어 있는 노드는 3번, 6번 노드이다. 그러므로 해당 간선을 제거한다. 그리고 진입차수 테이블을 아래와 같이 업데이트한다. 이 때 3번 노드는 진입차수가 0이된 반면 6번 노드는 아직 진입차수가 1이다. 그러므로 노드 3번만 큐에 집어넣는다.
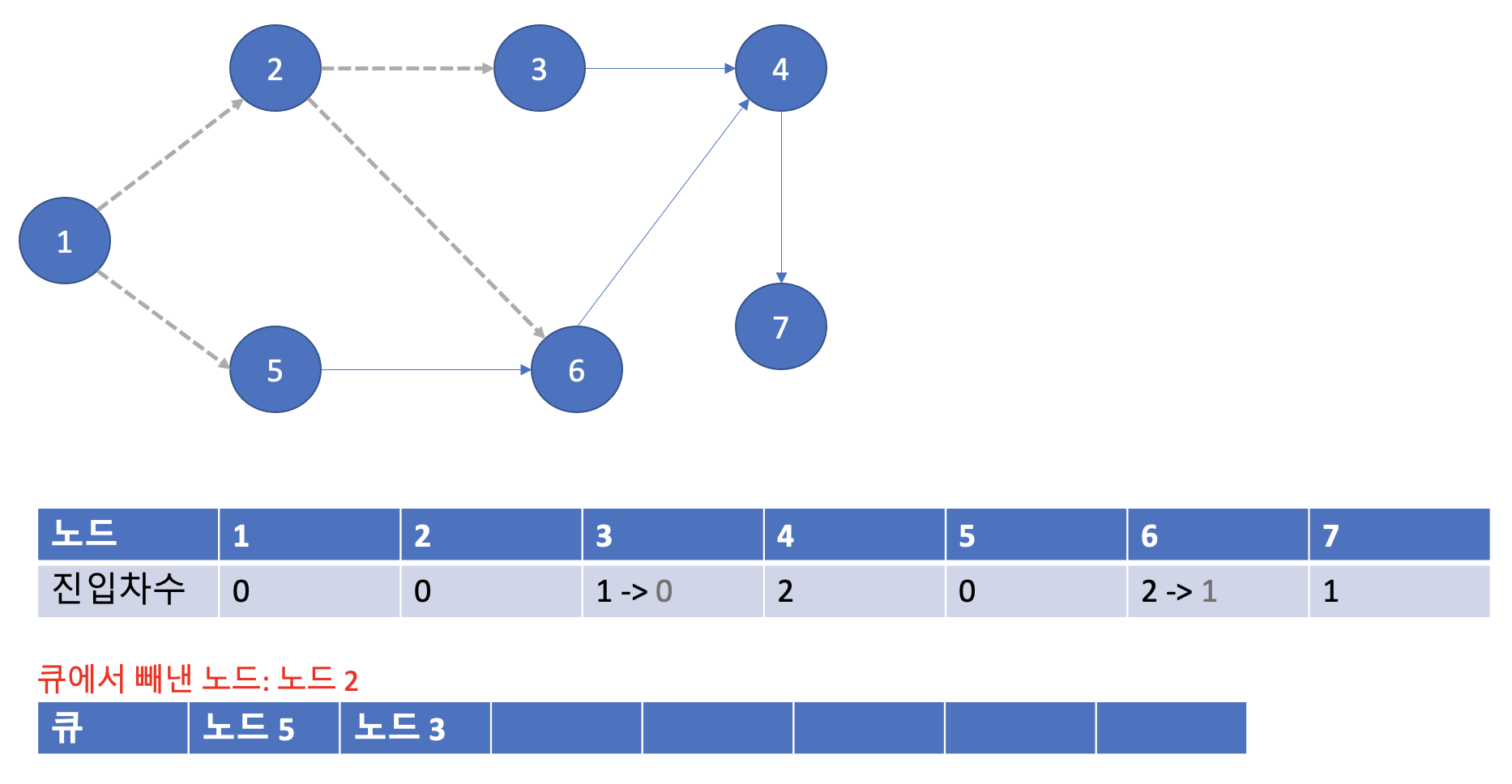
3-4. 네번째 단계
다음은 노드 5번을 빼낸다. 5번 노드와 연결되어 있는 노드는 6번 밖에 없다. 그러므로 해당 간선을 제거한다. 그리고 6번 노드의 진입 차수가 0이 되었으므로 6번 노드를 큐에 집어넣는다.
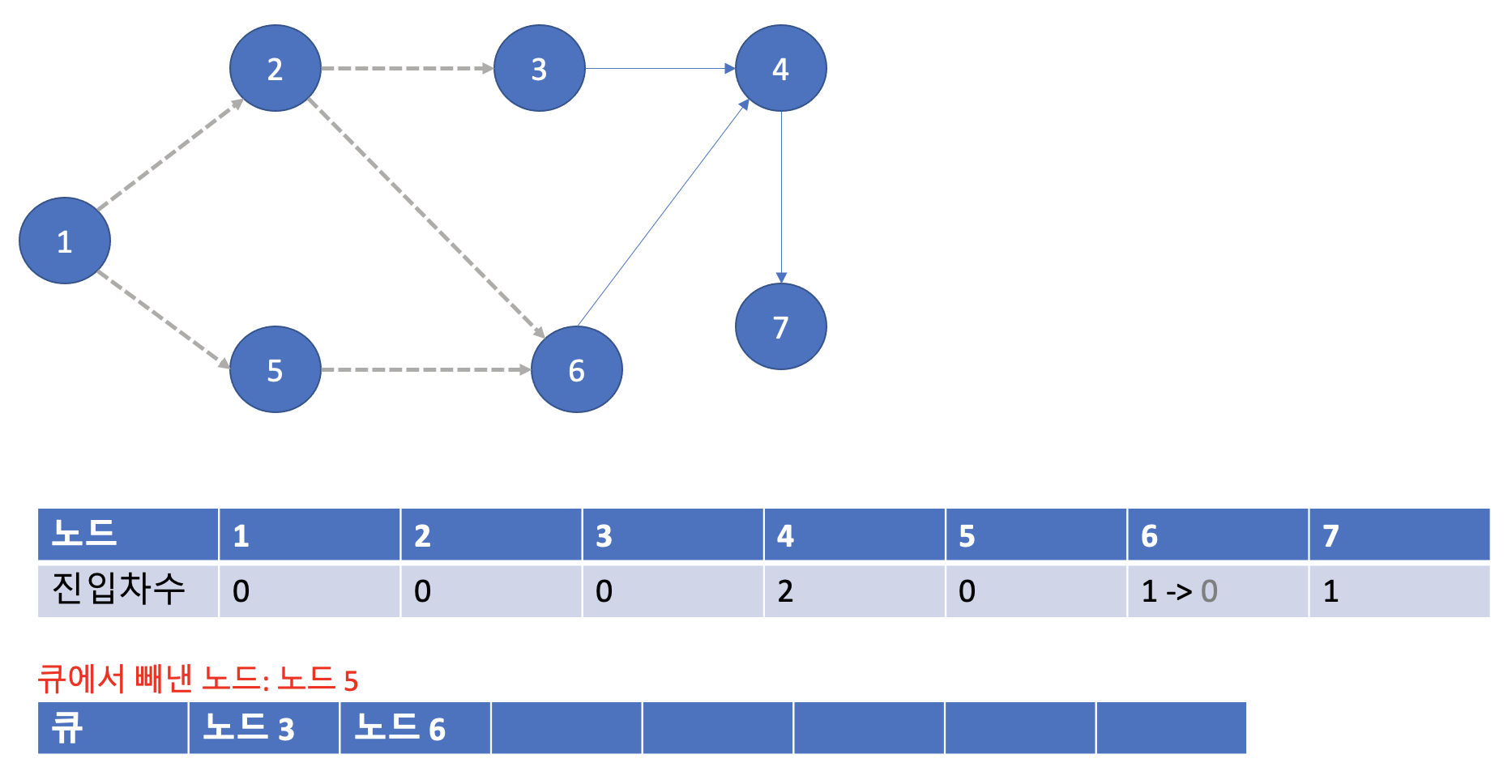
3-5. 다섯번째 단계
이제 노드 3을 큐에서 빼낸다. 그리고 노드 3과 4번 노드간에 연결되어 있는 간선을 제거한다. 그리고 아래와 같이 진입차수 테이블이 업데이트 된다. 그런데 업데이트한 진입 차수 중 0이 되는 노드가 없기 때문에 큐에 넣지 않고 넘어간다.
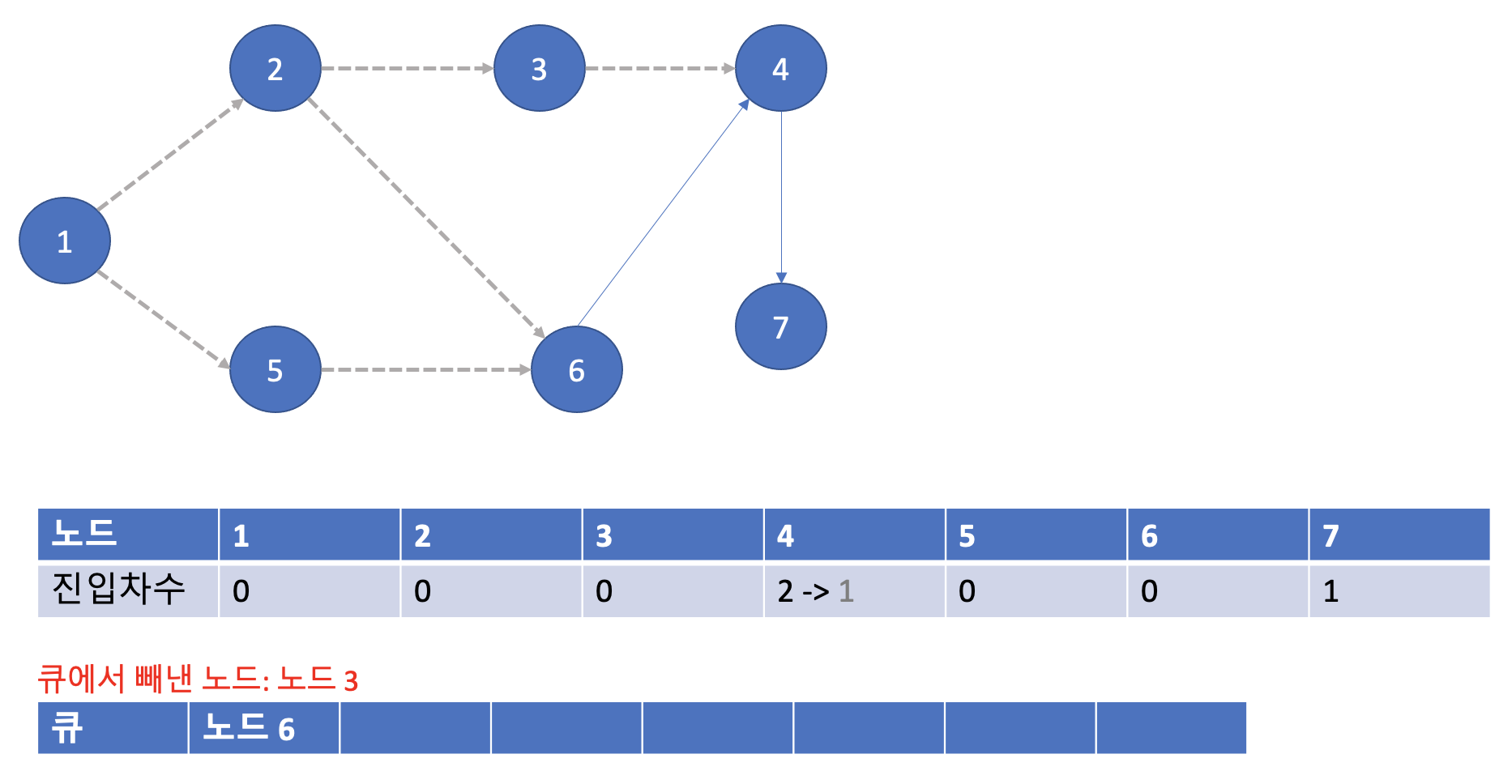
3-6. 여섯번째 단계
다음은 노드 6을 빼냈다. 노드 6과 연결되어 있는 노드는 4번이다. 그러므로 4번과 연결되어 있는 간선을 제거해 진입차수 테이블을 아래와 같이 업데이트 해준다. 그리고 4번 노드의 진입차수가 0이 되었으므로 큐에 4번 노드를 넣어준다.
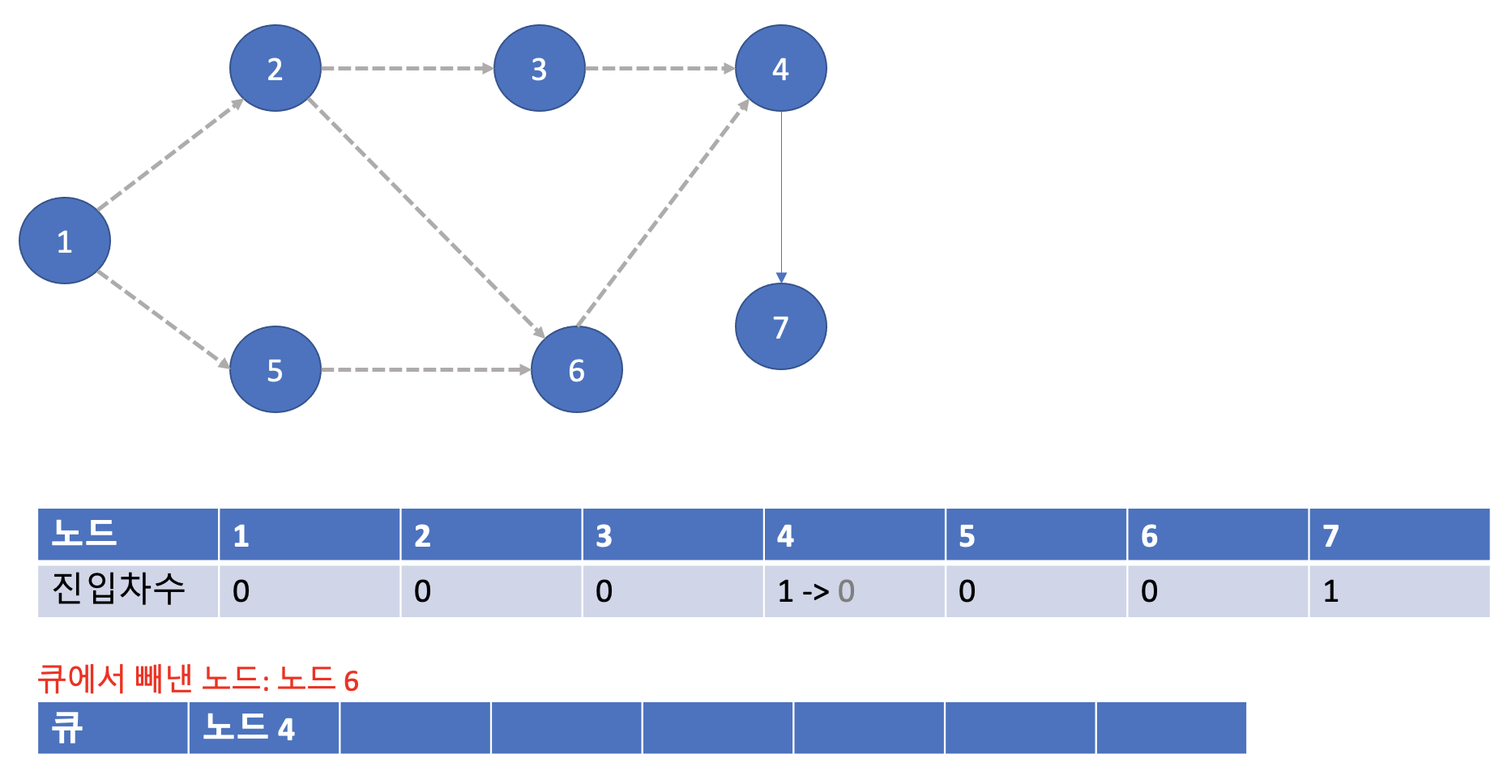
3-7. 일곱번째 단계
다음은 노드 4이다. 노드 4와 연결되어 있는 노드는 7번이다. 그러므로 해당 간선을 제거해 진입 차수 테이블을 아래와 같이 업데이트시켜준다. 그리고 7번 노드의 진입차수가 0이 되었기 때문에 큐에 넣어준다.
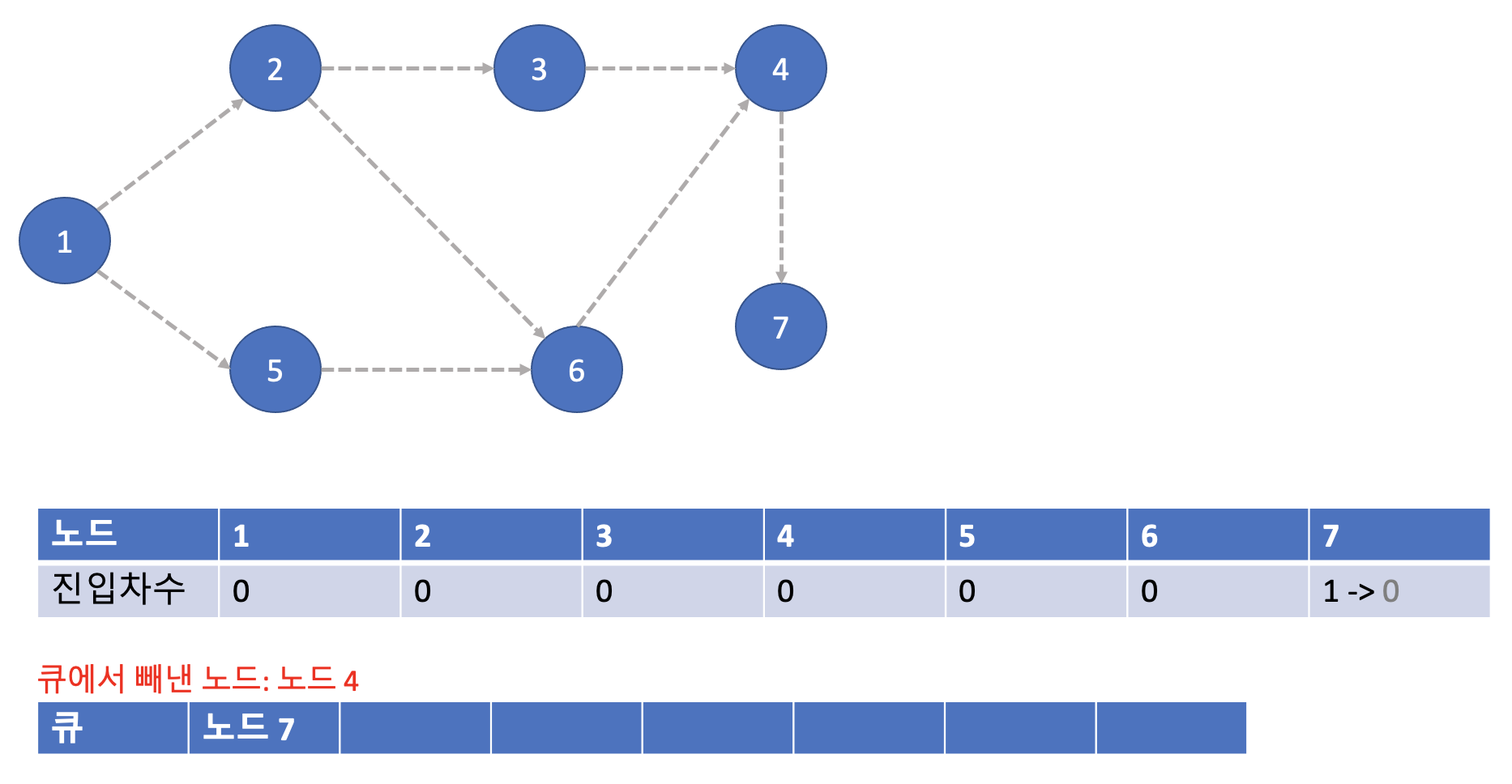
3-8. 여덟번째 단계
이번엔 노드 7번이다. 7번 노드와 연결되어 있는 노드는 아무것도 없다. 따라서 그냥 넘어간다. 그리고 이제 큐가 비어있으니 알고리즘이 종료된다.
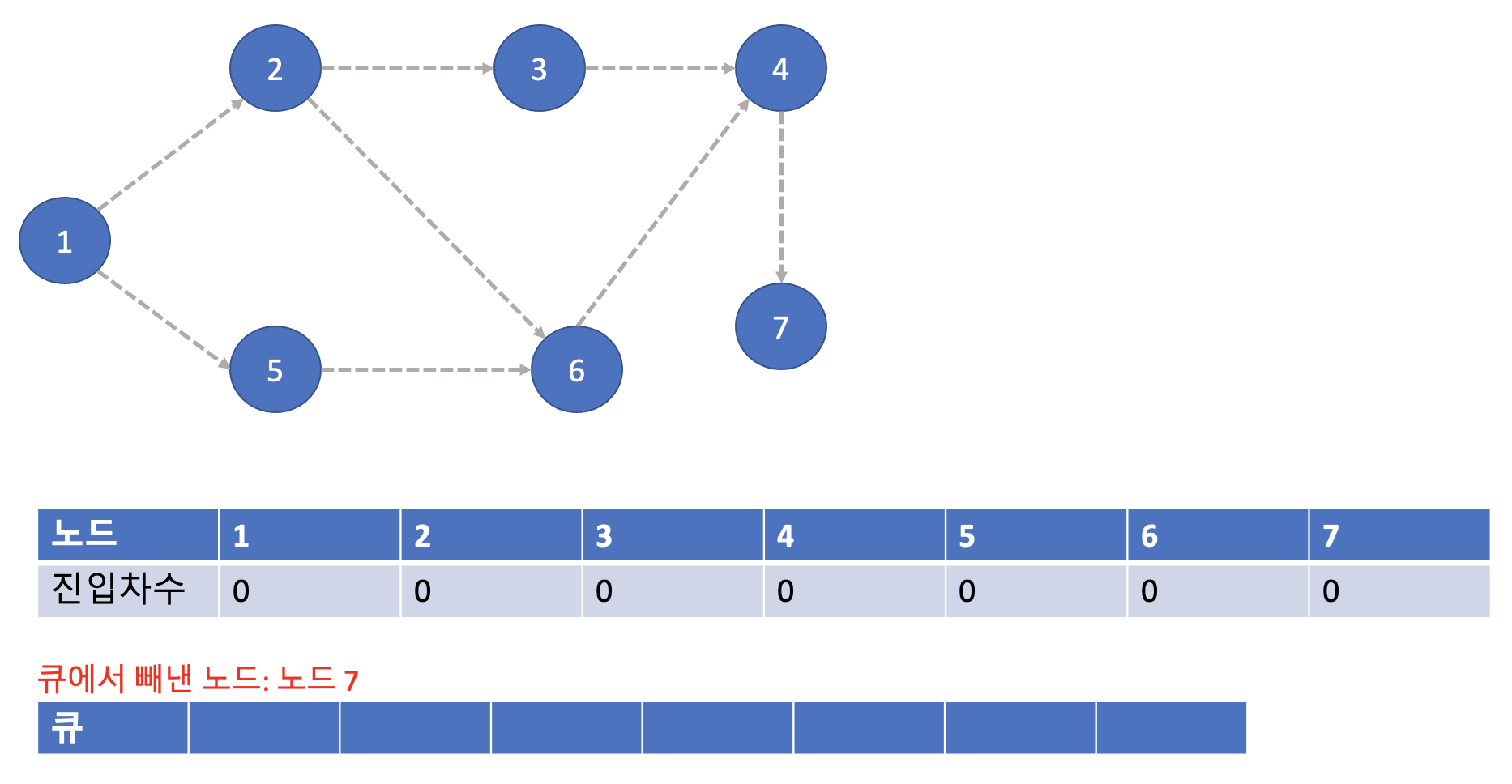
위 과정들을 수행하는 동안 큐에서 빠져나간 순서대로 노드 값을 출력하면, 그것이 바로 위상 정렬을 수행한 결과가 된다. 여기서 중요한 포인트는 위상 정렬의 결과값이 상황에 따라 여러가지 일 수 있다는 것이다. 위 알고리즘 단계에서는 하나의 단계에서 2개 이상의 노드가 큐에 동시에 들어간 적이 있다. 바로 2번, 5번 노드이다. 위 그림에서는 2번, 5번 중 번호가 작은 2번 노드를 먼저 넣었지만 5번을 먼저 넣게 된다면 위상 정렬 결과는 달라진다. 예시처럼 2번을 먼저 넣었다면 위상 정렬 결과는 1 -> 2 -> 5 -> 3 -> 6 -> 4 -> 7 이 되지만, 5번을 2번보다 먼저 큐에 넣게되면 결과는 1 -> 5 -> 2 -> 3 -> 6 -> 4 -> 7이 된다. 결국 2,5번 중 큐에 앞에 위치시키는 노드 순서가 먼저 오게 되어 정렬 결과가 나타난다. 따라서 한 번에 큐에 2개 이상의 노드가 들어갔다면 가능한 위상 정렬 결과는 여러가지가 된다.
참고로 위상 정렬 알고리즘의 시간 복잡도는 $O(V+E)$가 된다. 왜냐하면 처음에 진입차수가 0이 되는 노드를 찾기 위해 선형적으로 탐색해서 $O(V)$ 즉, 노드 총 개수만큼의 시간 복잡도가 소요된다. 그리고 큐에서 뺀 노드와 연결된 간선 개수($E$) 만큼 또 선형탐색하게 된다. 그래서 총 시간 복잡도는 $O(V+E)$가 된다.
4. 위상 정렬 Python으로 구현하기
from collections import deque
v, e = map(int, input().split())
# 진입 차수 테이블 초기화
indegree = [0] * (v+1)
# 그래프 데이터 담을 인접 리스트 초기화
graph = [[] for _ in range(v+1)]
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b)
# 진입차수 추가 a -> b이기 때문에 b입장에서 진입차수 +1
indegree[b] += 1
def topology_sort():
result = []
q = deque()
# 초기에 진입차수 0인 노드들 큐에 넣기
for i in range(1, v+1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌때 까지 반복
while q:
node = q.popleft()
# 꺼낸 원소는 위상 정렬 결과값에 append
result.append(node)
# 꺼낸 노드랑 연결된 노드들 탐색
for next in graph[node]:
indegree[next] -= 1
# 새롭게 진입차수가 0이 된 노드들 큐에 넣기
if indegree[next] == 0:
q.append(next)
for i in result:
print(i, end=' ')
topology_sort()'Python > 알고리즘 개념' 카테고리의 다른 글
| [Python] 가장 긴 증가하는 부분 수열 길이를 찾는 LIS 알고리즘 (0) | 2021.10.15 |
|---|---|
| [Python] 알아두면 좋을 기타 알고리즘 (0) | 2021.10.02 |
| [Python] 최소 신장 트리를 찾는 크루스칼(Kruskal) 알고리즘 (5) | 2021.09.29 |
| [Python] 그래프 알고리즘 - 서로소 집합 자료구조 (5) | 2021.09.27 |
| [Python] 모든 지점에서의 최단경로를 찾는 플로이드 워셜(Floyd-Warshall) 알고리즘 (0) | 2021.09.24 |



