🔊 해당 포스팅은 밑바닥부터 시작하는 딥러닝 2권의 교재 내용을 기반으로 자연어처리 딥러닝 신경망을 Tensorflow, Pytorch와 같은 딥러닝 프레임워크를 사용하지 않고 순수한 Numpy로 구현하면서 자연어 처리의 기초를 탄탄히 하고자 하는 목적 하에 게시되는 포스팅입니다. 내용은 주로 필자가 중요하다고 생각되는 내용 위주로 작성되었음을 알려드립니다.

저번 포스팅에서는 기본 RNN 모델에 게이트를 추가한 LSTM 모델에 대해 알아보았다. 이번 포스팅에서는 RNN에 게이트를 추가한 또 다른 모델인 GRU(Gated Recurrent Unit)에 대해 알아보자. 그리고 난 후, LSTM, GRU 등과 같은 게이트가 추가된 RNN 모델로 설계한 언어 모델(LM, Language Model)의 성능을 개선하는 몇 가지 방법에 대해서도 알아보자.
1. LSTM의 간소화 버전, GRU!
저번에 알아보았던 LSTM 모델은 아주 훌륭하게 긴 시계열의 패턴도 잘 학습할 수 있는 계층이었다. 하지만 이 LSTM도 단점이란 건 존재했으니.. 그것은 바로 학습할 파라미터가 많아져 계산이 상대적으로 오래걸린다는 것이다. 잠깐 그림을 통해 LSTM의 파라미터가 몇 개 였는지 다시 살펴보자.

위 그림을 보면 학습할 파라미터가 게이트들만 해도 12개가 된다.(각 게이트 당 파라미터 3개($W_x, W_h, b$)가 존재) 그래서 이러한 계산량이 많다는 단점을 보완하기 위해 등장한 모델이 바로 GRU(Gated Recurrent Unit)이다. GRU의 큰 아이디어는 다음과 같다. LSTM 처럼 게이트라는 기능은 유지하되, LSTM 보다 파라미터 개수를 줄이자! 그러면 LSTM과 GRU의 큰 구조적 차이점을 그림으로 비교해보자.

GRU 구조 그림을 보면 LSTM에서 존재했던 기억 셀($c$)이 사라진 것을 볼 수 있다. 즉, 은닉 상태 벡터($h$)만을 사용해 전달받고 보내면서 게이트를 적용하게 된다. 구조 자체만 보면 기본 RNN 구조와 동일하다. 그러면 이제 GRU 구조를 하나하나씩 뜯어보자.
2. GRU의 구조 뜯어보기
GRU의 완성된 구조는 아래와 같다.

위 그림을 보면 GRU는 총 2개의 게이트를 갖는다. 첫 번째는 Reset gate, 두 번째는 Update gate 이다. 이제 이를 하나하나 살펴보자.
2-1. 과거의 은닉 상태($h$)가 갖고 있는 정보를 얼마나 받아들이지? Reset 게이트!
가장 첫 번째로 하단의 노락색 네모칸의 리셋 게이트부터 알아보자. 리셋 게이트는 이전 시각의 은닉 상태 벡터($h_{t-1}$)를 얼마나 무시할지를 결정한다. 다시 말해, $h_{t-1}$이 갖고 있는 정보 중 어느 정도만 믿고 받아들일지 결정하는 셈이다.
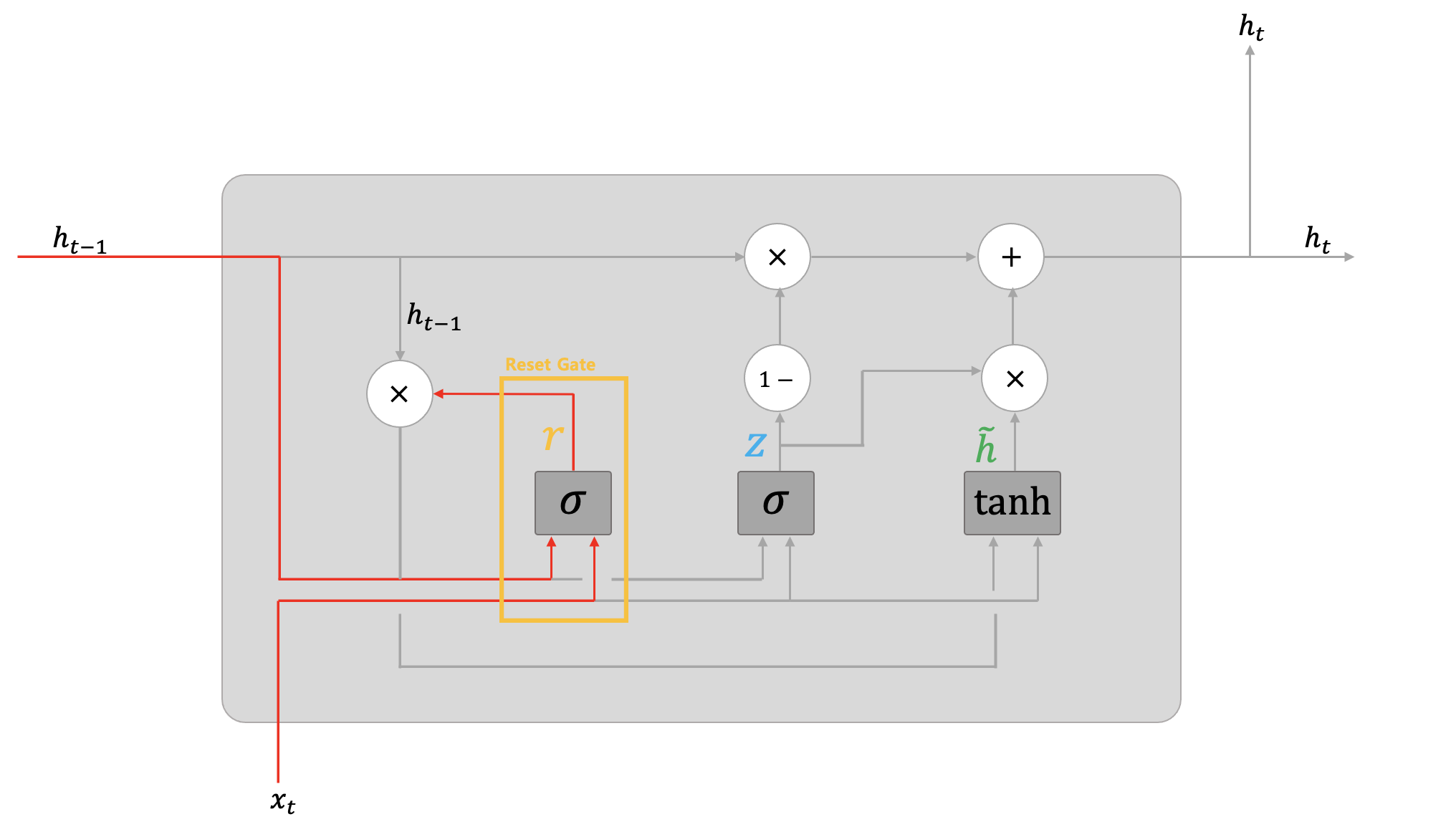
추후에 Update 게이트 값인 $\tilde{h}$를 설명하면서 다시 언급하겠지만 $\tilde{h}$를 계산하는 수식을 보면 리셋 게이트값인 $r$이 아마다르 곱으로 $h_{t-1}$과 곱해지는 것을 볼 수 있다. 이 때, 만약 $r$ 값이 0 즉, 이전 은닉 상태 정보를 모두 무시해! 라고 한다면 업데이트 게이트값인 $\tilde{h}$을 계산할 때, $h_{t-1}$은 0인 $r$과 곱해져 사라지는 것을 알 수 있다. 그래서 리셋 게이트 값($r$)이 바로 '이전 은닉 상태 벡터의 정보를 얼마나 받아들일지'를 의미하게 된다.
그러면 리셋 게이트 값인 $r$을 계산하는 수식을 살펴보자. 위 그림을 보면 $r$을 계산하기 위해서 이전 은닉 상태 벡터인 $h_{t-1}$과 현재 시점의 입력 벡터인 $x_t$가 관여하는 것을 알 수 있다.
$$r = \sigma(x_t {W_x}^{(r)} + h_{t-1} {W_h}^{(r)} + b^{(r)})$$
수식을 보면 LSTM에서 게이트를 설명했을 때와 동일하게 GRU의 리셋 게이트에도 추가 파라미터 3개(${W_x}^{(r)}, {W_h}^{(r)}, b^{(r)}$)가 존재한다. 학습 데이터를 통해 이 3개의 파라미터를 학습시키면서 최적의 리셋 게이트 값인 $r$을 최적화 해나간다. 그리고 게이트 값(열림 상태)을 0.0 ~ 1.0 사이의 실수값으로 표현하기 위해 $\sigma$ 활성함수를 적용한다.
그리고 난 후, 분기되어 흘러가고 있는 이전 은닉 상태 벡터 $h_{t-1}$과 아다마르 곱을 수행해주어 '은닉 상태 벡터의 정보를 얼마나 받아들일지'를 적용한다.
2-2. 과거의 은닉 상태($h$)를 갱신시키자, Update 게이트!
다음은 과거의 은닉 상태($h_{t-1}$)를 갱신시키는 업데이트 게이트이다. 여기서 '갱신'이란, 과거 은닉 상태 벡터와 현재 시점의 입력 벡터가 흘러들어오면서 불필요한 정보는 잊어버리고 필요한 정보만을 취사선택하는 것을 의미한다. LSTM으로 비교하자면, LSTM에서의 Forget, Input 게이트의 역할 2개를 GRU에서는 Update 게이트가 한 번에 수행한다. 그래서 여기서는 업데이트 게이트가 2가지 역할(Forget, Input)을 수행하기 때문에 하나씩 파트별로 살펴보도록 하자.
먼저 아래 그림의 파란색 네모칸 부분이다. 이 부분은 LSTM에서의 Forget 게이트와 같은 역할을 담당한다.
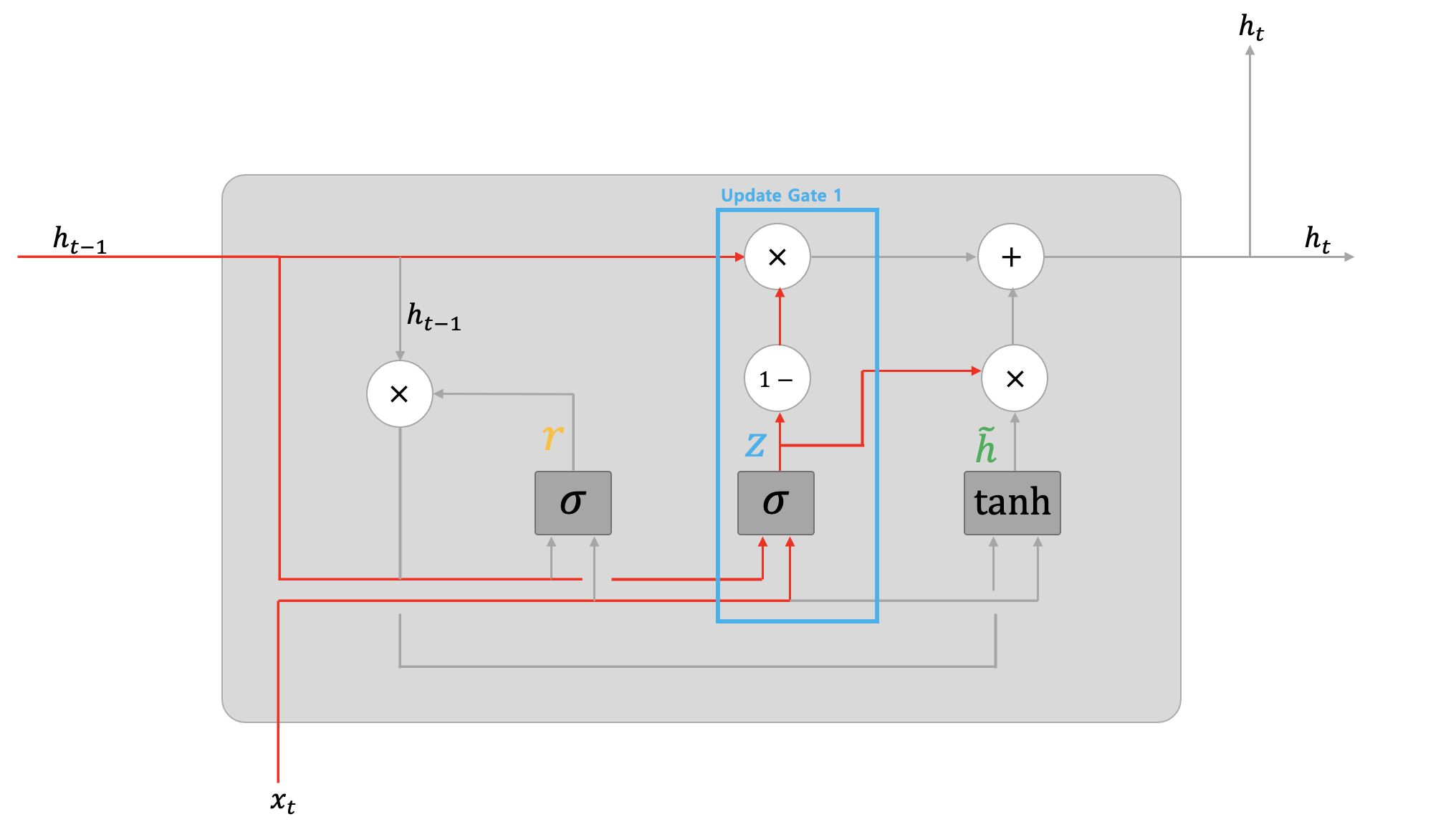
우선은 업데이트 게이트 값 중 하나인 $z$를 계산하는 수식을 살펴보자.
$$z = \sigma(x_t {W_x}^{(z)} + h_{t-1} {W_h}^{(z)} + b^{(z)})$$
그동안 배웠던 게이트 수식과 다를 바 없다. 이 역시 추가 파라미터 3개(${W_x}^{(z)}, {W_h}^{(z)}, b^{(z)}$)를 두어 최적의 게이트 값을 찾아나갈 수 있다. 그리고 활성함수로 $\sigma$를 사용하여 0.0 ~ 1.0 사이의 실수 값으로 바꾸어 준다.
그렇게 계산된 $z$ 값은 두 갈래로 분기된다. 한 쪽은 $1 - $ 연산을 통과하면서 $1-z$로 바뀐 후 흘러가고 있는 이전 은닉 상태 벡터인 $h_{t-1}$과 아다마르 곱을 수행해주어 최종 수식이 $(1-z) \odot h_{t-1}$이 된다. 이 수식은 곧 은닉 상태 벡터에서 불필요한 정보를 얼마나 잊어버릴지를 적용한 것을 의미한다.
나머지 한 쪽은 다음에 알아볼 업데이트 게이트 중 또 다른 값인 $\tilde{h}$과 연관되어 있다. 그러면 이 타이밍에서 나머지 업데이트 게이트 값인 $\tilde{h}$ 부분에 대해 알아보자. 아래 그림의 초록색 네모칸을 의미하는데, 이 부분이 LSTM에서의 Input 게이트와 같은 역할을 한다.
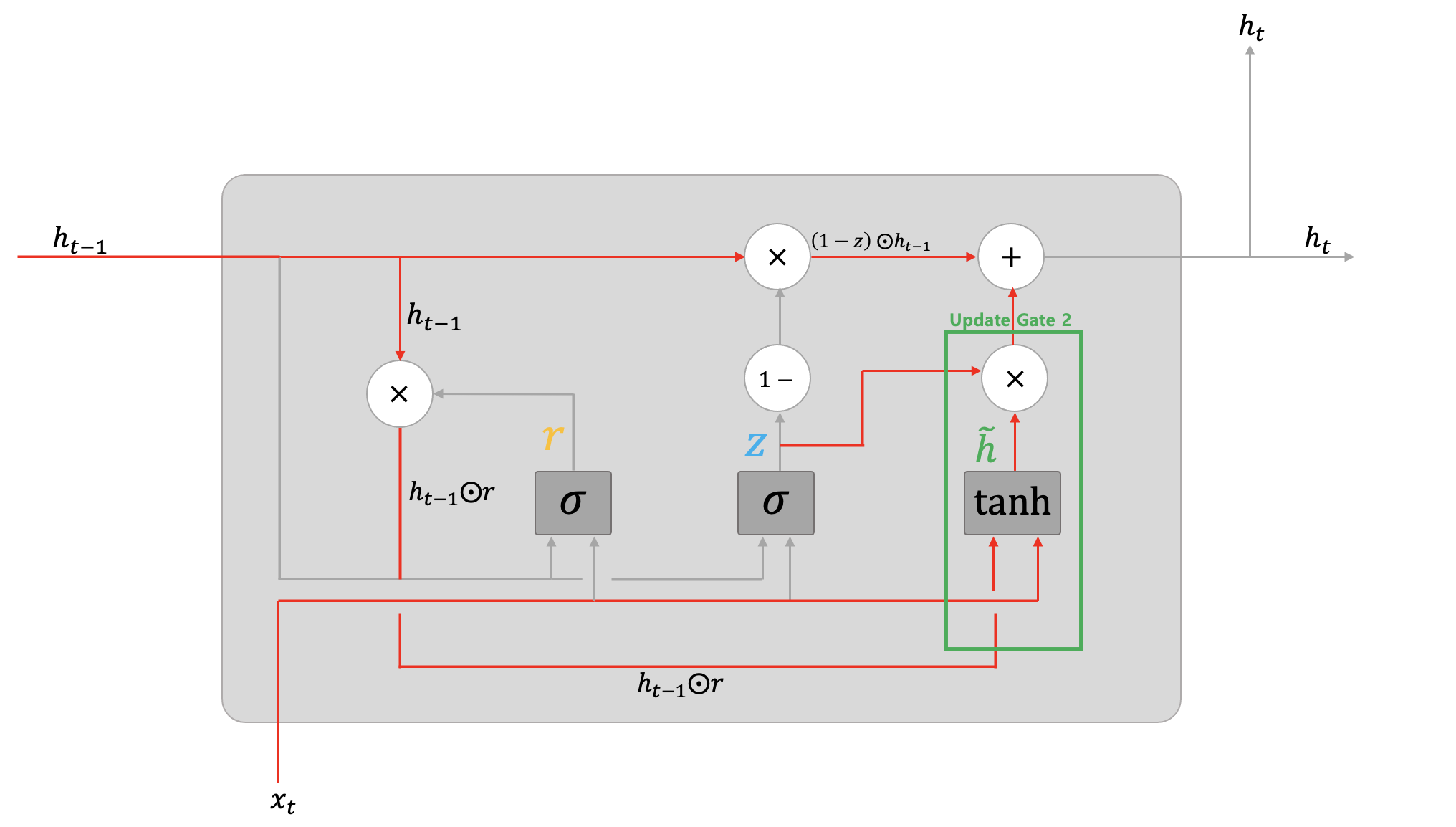
위 그림을 보면 업데이트 게이트의 두 번째 값인 $\tilde{h}$는 계산된 리셋 게이트 값($r$)과 업데이트 게이트의 첫 번째 값인 $z$ 값과 입력 벡터 $x_t$가 관여하는 것을 볼 수 있다. 구체적으로, 리셋 게이트 값과 관련된 값인 $h_{t-1} \odot r$이 관여하며, 업데이트 게이트의 첫 번째 값인 $z$와 입력 벡터 $x_t$가 직접 관여하는 것을 볼 수 있다. 그래서 업데이트 게이트의 두 번째 값인 $\tilde{h}$를 계산하는 수식을 작성하면 아래와 같다.
$$\tilde{h} = tanh(x_t W_x + (h_{t-1} \odot r)W_h + b)$$
위 수식으로 계산된 $\tilde{h}$는 업데이트 게이트의 첫 번째 값인 $z$와 아다마르 곱을 수행한다. 그리고 GRU의 최종 출력 값인 $h_t$를 아래처럼 계산한 후, 다음 GRU 계층으로 전달한다.
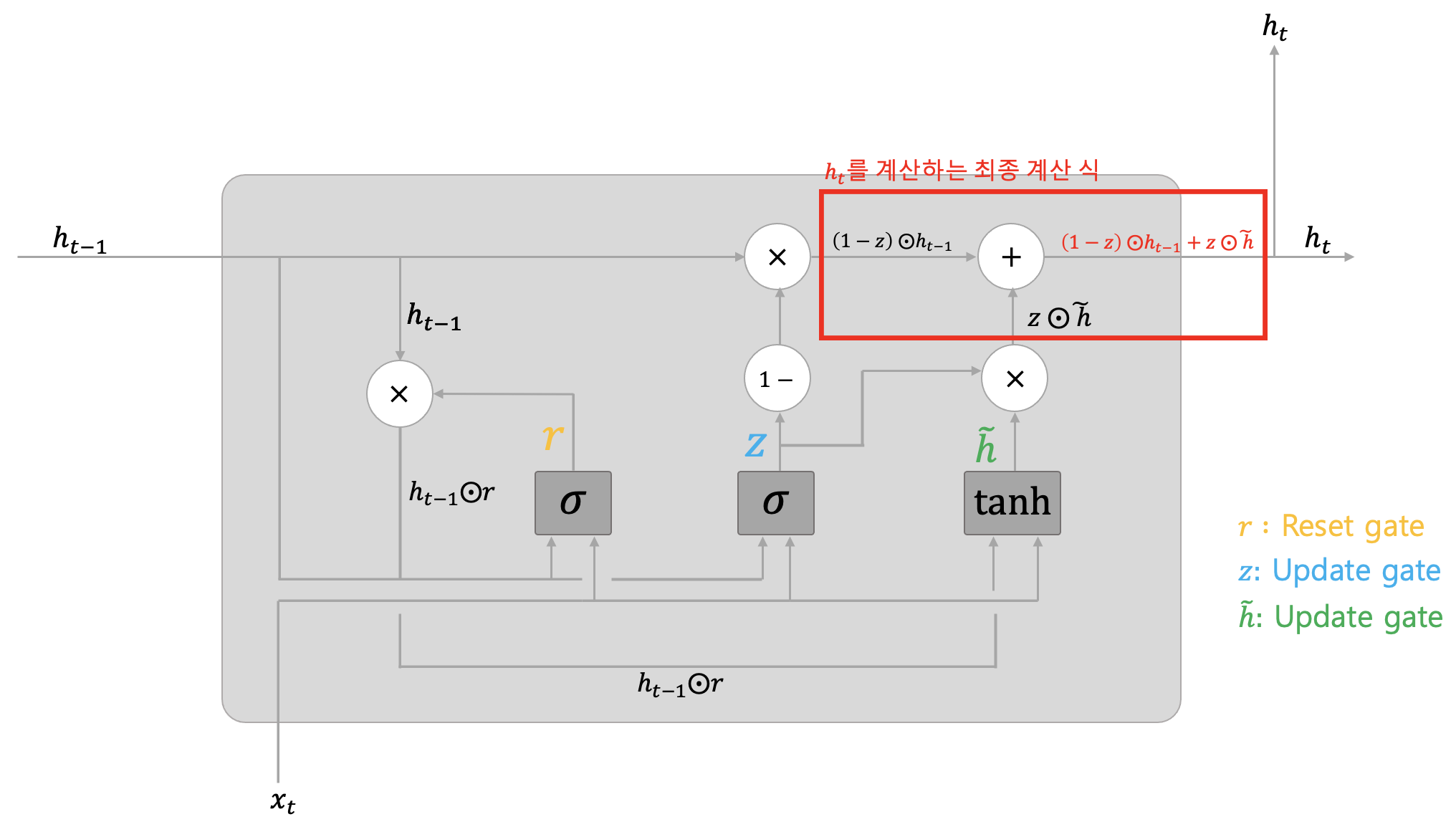
2-2. 계산그래프를 통해 GRU의 역전파 이해하기
그러면 이제 GRU의 역전파를 계산 그래프를 통해서 이해해보자. 이에 대해서는 책에는 나와있지 않지만 필자가 직접 계산해서 작성한 역전파 계산 그래프이다.(혹시라도 계산 식에 오류가 있다면 댓글 남겨주시면 감사하겠습니다!)
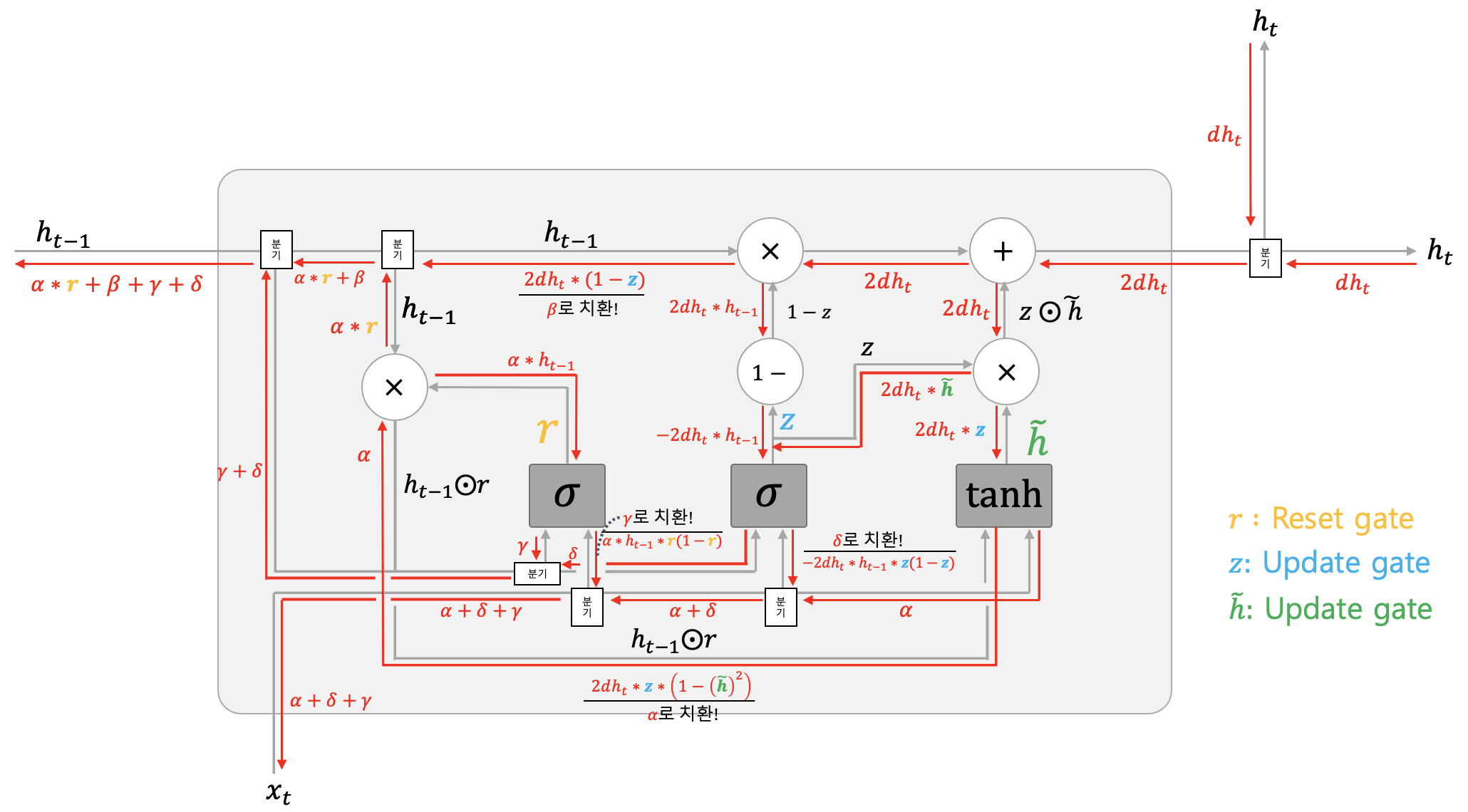
위 그림에서 리셋 게이트 값을 나타내는 $r$ 과 $\gamma$ 기호가 헷갈릴 수도 있어서 게이트 값들은 전부 게이트 색깔에 맞게 가시적으로 잘 표시를 해놓았다. 역전파 방향으로 그동안 배워왔던 다양한 연산 노드의 역전파 계산 방식을 적용해보면 생각보다 쉽게 위처럼 계산해낼 수 있다. 개인적으로 한 번 계산해보길 강추한다! 이렇게 해놓으면 넘파이로 구현한 코드를 볼 때 이해가 정말 빨리 된다. GRU를 넘파이로 구현한 코드는 여기를 참조하자.
3. RNN LM 모델 성능 개선하기
이번 목차에서는 그동안 배웠던 기본 RNN, LSTM, GRU와 같은 순환신경망 계열의 모델로 만들 수 있는 언어 모델(LM)의 성능을 더 개선시킬 수 있는 방법 3가지에 대해 알아보자.
3-1. 순환신경망을 겹겹이 쌓아보자, 계층 다층화!
첫 번째 방법은 순환신경망을 겹겹이 쌓는 계층 다층화 방법이다. 이는 그림으로 보면 계층을 다층화한다는 것이 무엇인지 이해할 수 있다. 하단의 그림은 LSTM 계층을 사용한다고 가정했을 때의 그림이다.
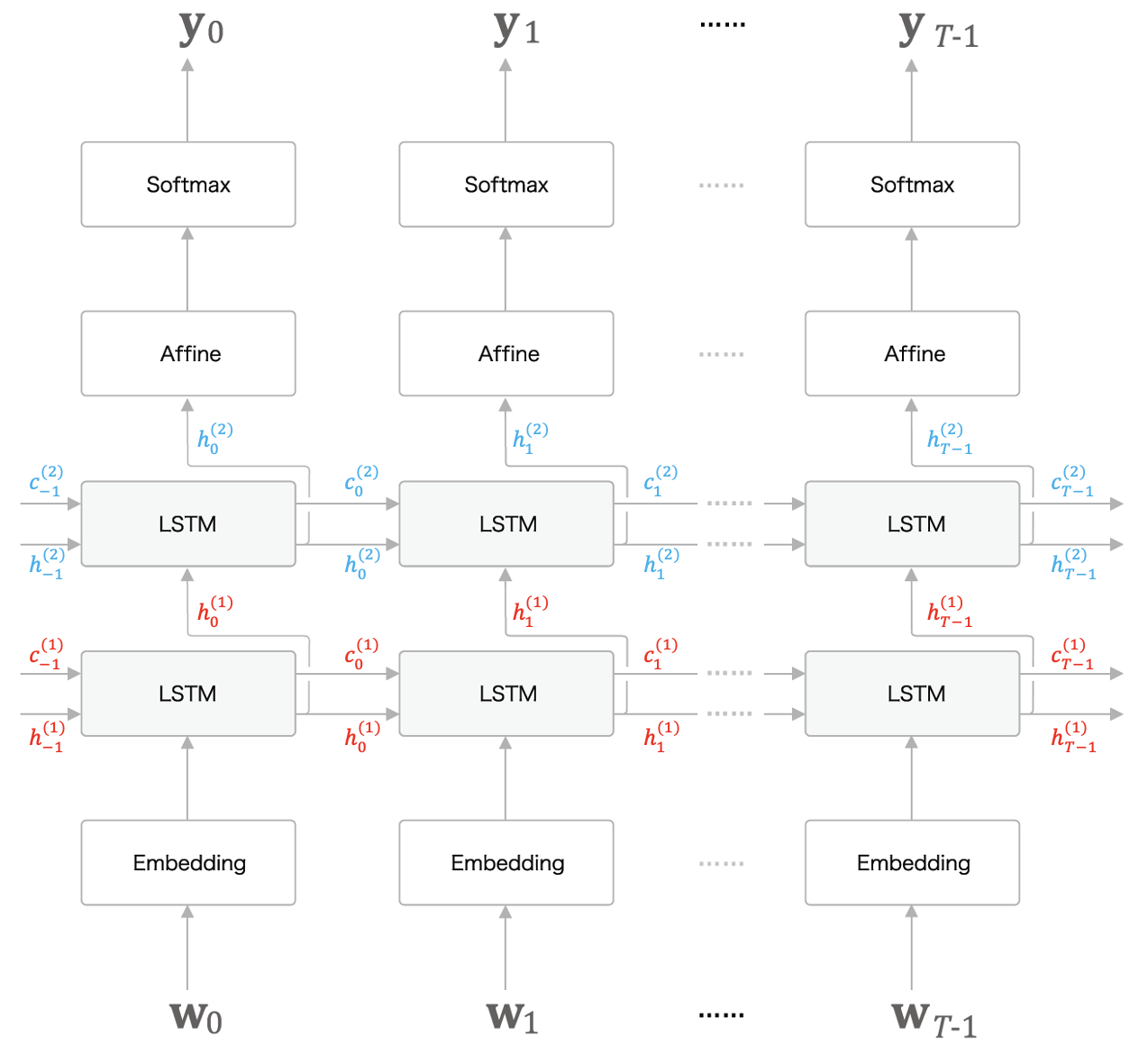
그림을 보면 LSTM 계층 위에 또 다른 LSTM 계층이 존재하는 것을 알 수 있다. 즉, 가장 아래층에 있는 LSTM 계층의 은닉 상태 벡터 값을 위 층의 LSTM 계층의 입력 값으로 넣어주는 것이다. 이렇게 순환신경망을 다층화하여 구조를 형성하면 단층일 때보다 더 복잡한 패턴을 파악할 수 있다고 한다. 참고로 현재는 쓰이는지 잘 모르겠지만 구글 번역에 사용된 GNMT 모델은 이 LSTM 계층을 8층으로 쌓은 모델이라고 한다.
3-2. Dropout을 활용한 모델의 과적합 예방
드롭아웃은 모델을 학습시킬 때, 신경망 모델의 노드 중 랜덤하게 일부를 삭제하여 모델의 성능에 정규화(Regularization)를 적용하는 기술이었다. 밑시딥 1권을 공부했을 때 등장하기도 한 개념이며 넘파이로 구현해 본 적도 있었다. RNN(순환 신경망) 계열의 모델들은 일반적인 Feed-Forward 신경망보다 상대적으로 과적합 되기 쉽다고 알려져 있다.(개인적으로 '시계열' 이라는 특성 때문에 그런 듯 하다. 시계열은 앞쪽에서 오류가 발생하면 연쇄적으로 계속 오류가 발생하기 때문에 그렇지 않을까?) 그래서 RNN 모델의 과적합 해결은 그만큼 중요한 이슈이다.
모델 성능의 과적합을 예방하기 위한 방법으로는 대표적으로 학습 데이터 양 자체를 늘린다거나 모델의 복잡도를 줄이기(파라미터 개수를 줄이는 등) 또는 모델의 파라미터에 패널티는 주는 정규화 기법이 있다. 드롭아웃은 이 중 정규화 기법에 속한다.
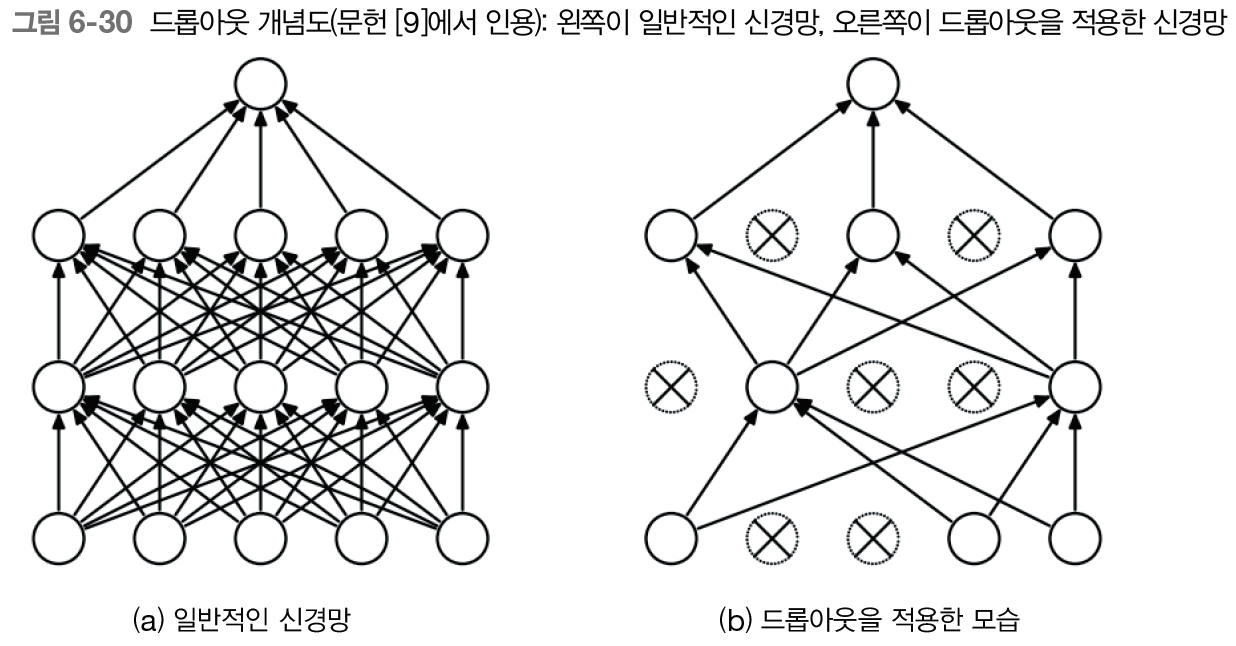
우선 피드 포워드 신경망일 때 드롭아웃을 모델 어느 곳에 삽입했는지 다시 상기시켜보자.
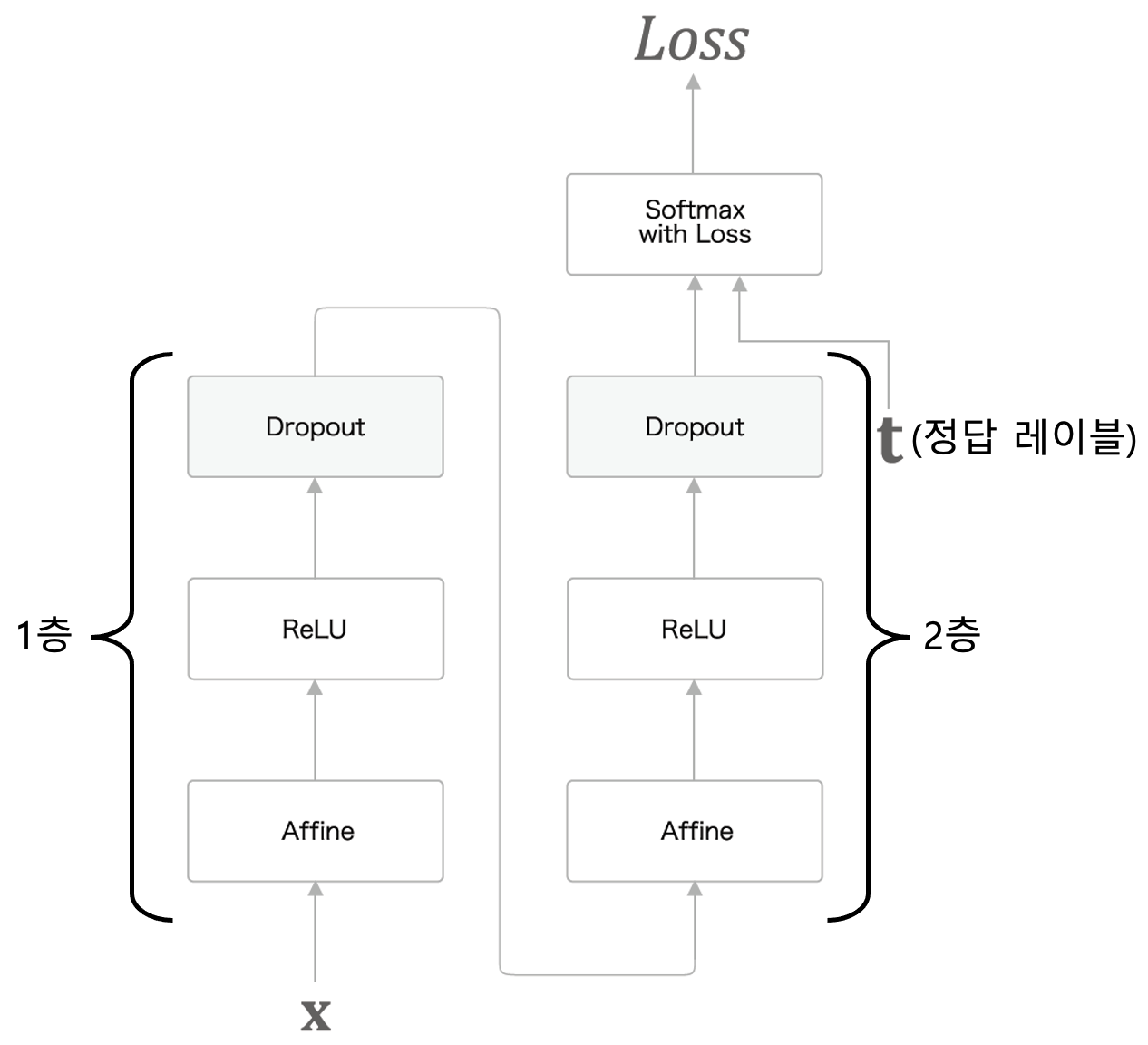
위 그림을 보면 피드-포워드 신경망일 경우, 각 층의 활성함수 다음에 적용했던 것을 알 수 있다. 그러면 이와 똑같은 방식으로 LSTM에 드롭아웃 계층을 삽입하면 아래와 같아진다.
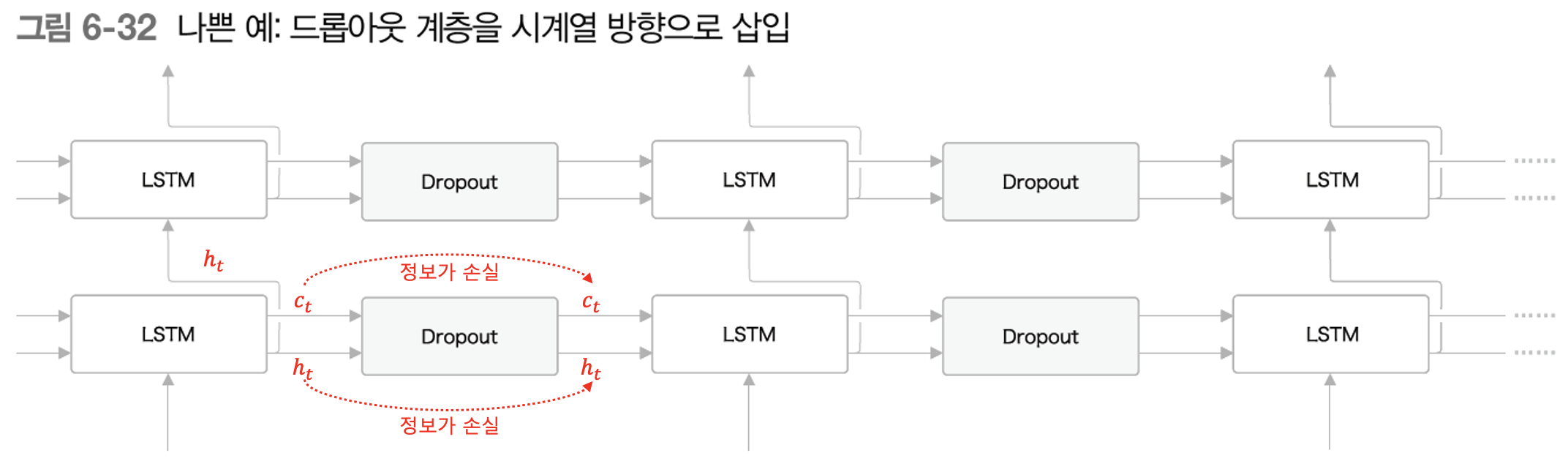
위 그림처럼 시계열 방향으로 드롭아웃 계층을 삽입하면 LSTM 계층이 순환되면서 나오는 은닉 상태 벡터($h_t$)와 기억 셀($c_t$)이 드롭아웃 계층을 통과해 나오면서 정보가 손실 될 가능성이 높아진다. 하나의 드롭아웃 계층만 통과해도 정보가 손실되는데 이를 계속 순환하면서 드롭아웃 계층도 계속 적용하게 되면 나중에는 남아 있는 유의미한 정보가 아예 존재하지 않을 것이다.
그래서 RNN 계열의 신경망을 활용할 때 드롭아웃 계층을 넣어야 하는 위치는 시계열 방향이 아닌 상하 방향(깊이 방향)이다. 상하 방향에 삽입한다는 것은 아래 그림처럼을 의미한다.
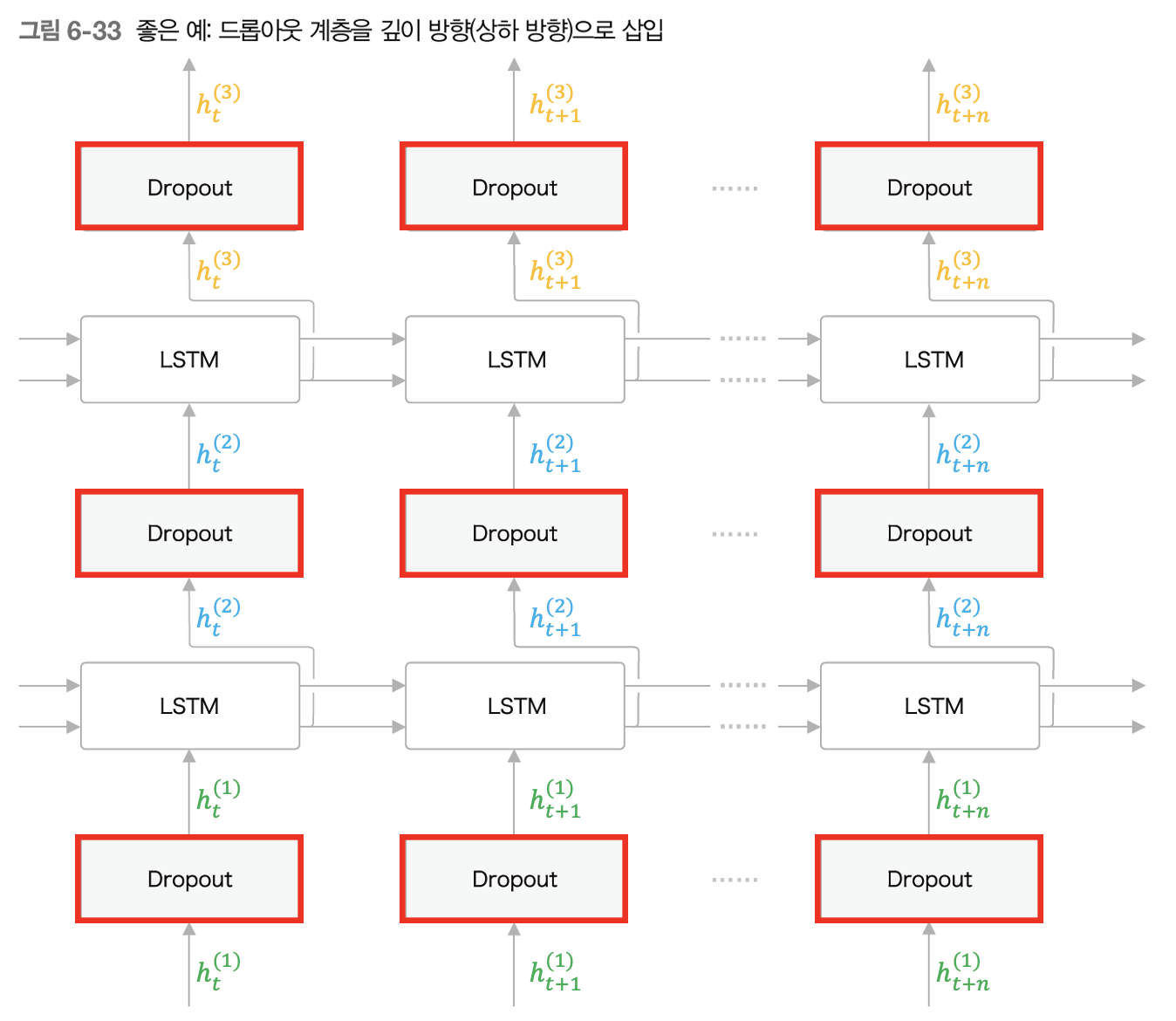
위 그림처럼 드롭아웃 계층을 위쪽으로 출력되는 은닉 상태 벡터($h$)에만 적용하는 것이다. 이렇게 구성하게 되면 좌,우 방향 즉, 시간 방향으로 아무리 진행해도 순환하는 LSTM 신경망 사이에 전달 되는 은닉 상태 벡터($h$)와 기억 셀($c$)의 정보가 손실되지 않는다.
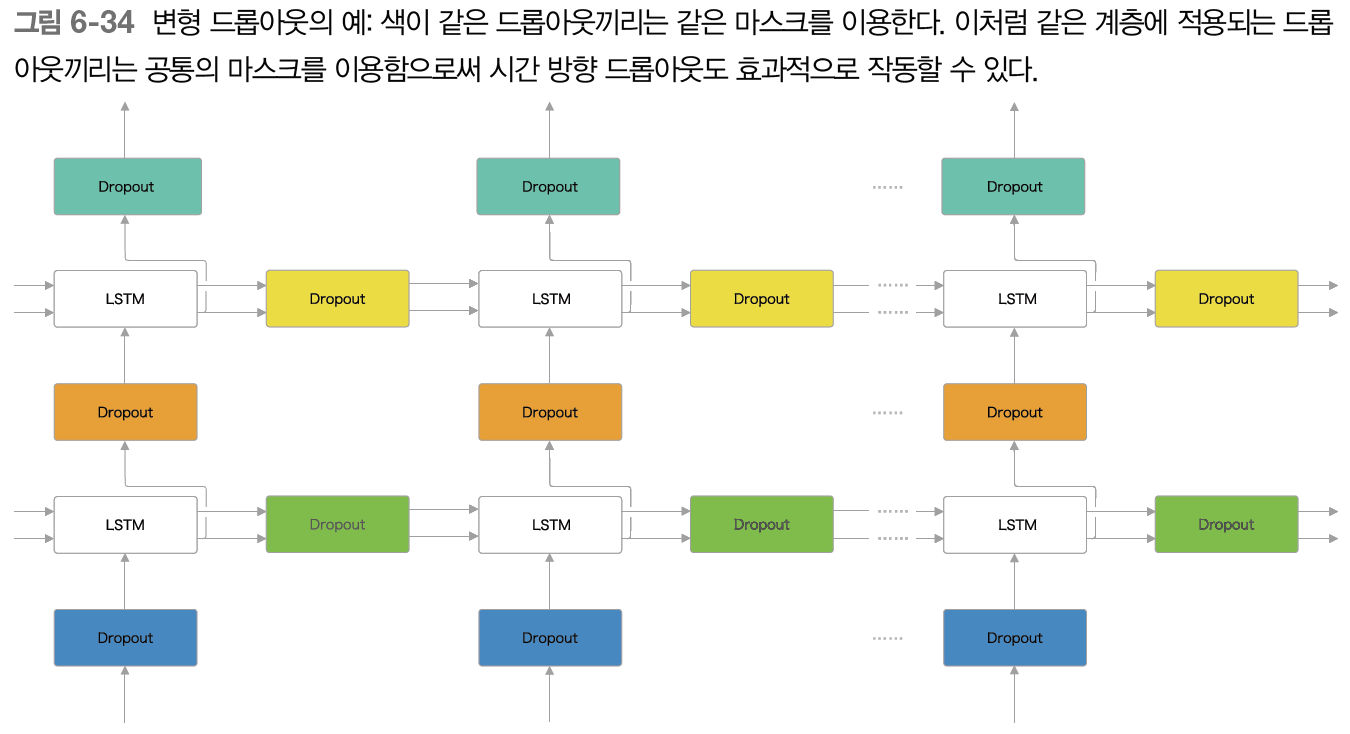
추가적으로 책에서는 위 기법들을 기반으로 하는 변형 드롭아웃 기법을 소개하기도 한다. 상,하(깊이) 방향으로 드롭아웃 계층을 넣는 기법은 유지하되 좌,우(시간) 방향으로 드롭아웃 계층을 삽입하는데 이 때는 같은 계층에 속한 드롭아웃들은 같은 마스킹(masking)을 공유하도록 한다. 여기서 '같은 마스킹을 공유'한다는 것은 같은 계층끼리는 삭제할 노드를 통일시킨다는 것이다.
3-3. 가중치 공유(Weight tying)
마지막으로는 한 계층의 가중치를 다른 계층에서 공유함으로써 모델 성능의 과적합을 예방할 수 있다. 이는 컴퓨터 비젼의 Resnet 모델에서 처음 제안한 Skip connection 개념과 매우 유사하다. LSTM에서의 가중치 공유를 도식화하면 아래와 같다.
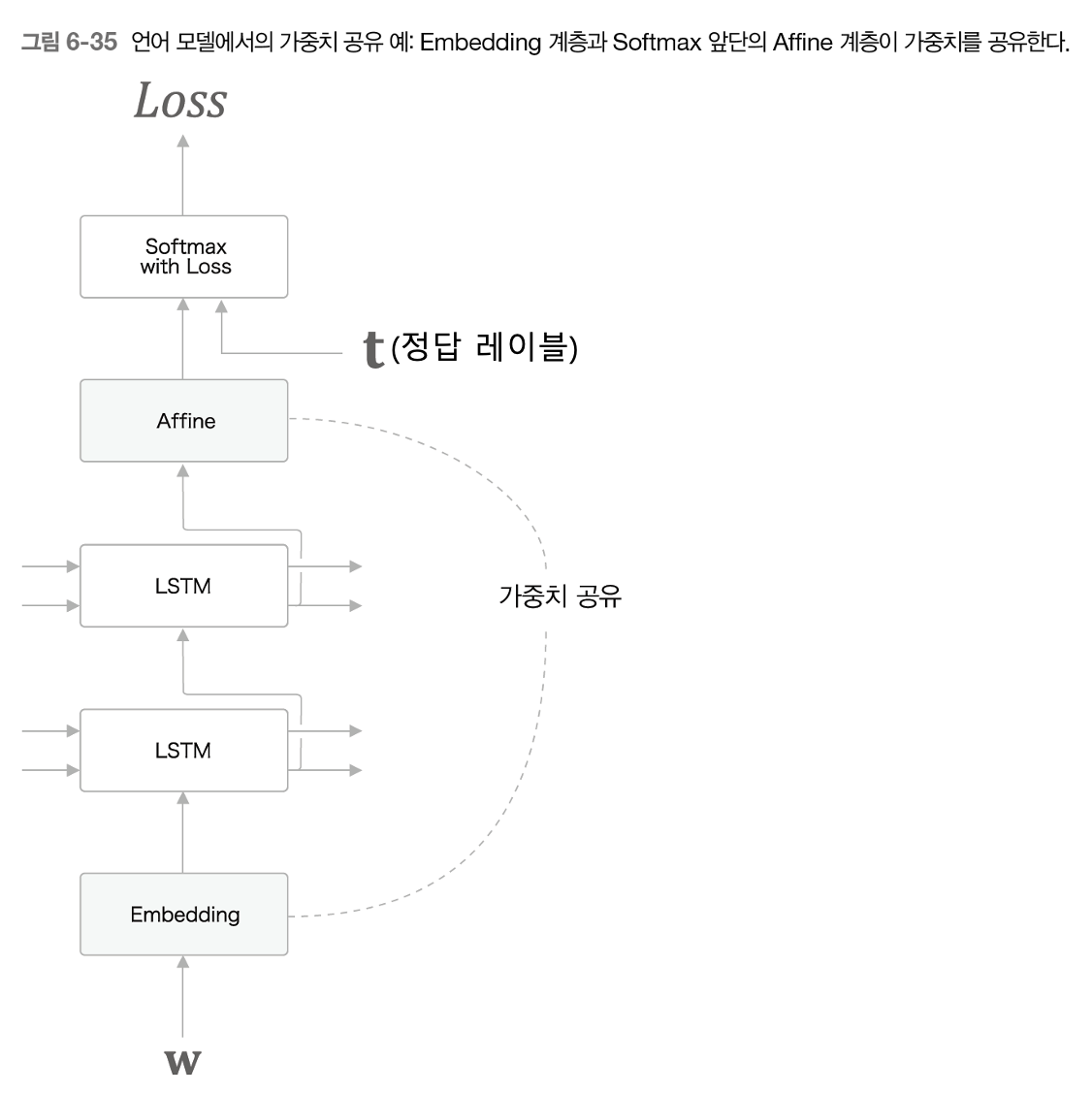
위 그림에서는 $w$를 입력으로 받는 Embedding(임베딩) 계층의 가중치를 모델 마지막 부분의 Affine(행렬 곱) 계층에서 활용한다. Resnet 이미지 분류 모델의 Skip Connection과 차이점이 있다면 Skip Connection은 이전 계층의 출력값을 현재 계층의 출력값에 더해주는 것이지만 여기에서의 가중치 공유 기법은 두 계층이 동일한 파라미터 값을 이용한다는 것이다. 위 그림으로 설명하자면, 임베딩 계층과 Affine 계층의 파라미터는 동일하며 갱신될 때도 같은 값으로 갱신되는 것이다.
이렇게 되면 각각 파라미터를 갖고 있었던 두 개의 계층이 하나의 파라미터만 사용하게 되는 셈이다. 따라서 파라미터 개수가 줄어듦으로써 모델 복잡도가 이전보다 낮아지면서 테스트 데이터에 대한 정확도도 향상되는 효과(과적합 예방!)가 발생한다.
가중치 공유를 넘파이로 구현한다는 상황이라고 했을 때, 두 계층의 파라미터 형상을 상상해보자. 먼저 임베딩 계층의 파라미터 형상이 $(V, H)$라고 가정해보자. 이 때, $V$는 임베딩 계층의 노드(차원) 수, $H$는 LSTM 계층 내의 노드 수 즉, 은닉 상태 벡터의 차원 수를 의미한다. 이 때, Affine 계층(행렬 곱)의 파라미터 형상은 $(H, V)$가 된다. 즉, 임베딩 계층 파라미터 형상($(V, H)$)의 전치행렬이 되게 된다! 그러므로 구현할 때 임베딩 계층의 파라미터를 전치행렬 해주게 되면 곧 그것이 Affine 계층의 파라미터가 된다.
지금까지 알아본 RNN 언어 모델의 성능 개선 기법을 적용한 예시 모델을 구현하는 코드는 저자코드를 참조해보자.
이번 포스팅을 통해 게이트가 추가된 또 다른 모델인 GRU의 구조와 역전파 방식에 대해서도 알아보았다. 또한 GRU, LSTM과 같은 RNN 계열의 신경망을 활용해 만든 언어 모델의 성능을 개선하는 방법에 대해서도 알아보았다.
다음 포스팅에서는 RNN을 사용한 '문장 생성'을 알아본다. 지금까지는 단순히 다음에 나올 '단어'만을 예측해보았다. 이제 '문장' 단위로 예측하는 방법에 대해서도 알아보자. 또 더 나아가 Encoder - Decoder 구조로 구성되는 seq2seq 모델에 대해서도 알아보자.
'Data Science > 밑바닥부터시작하는딥러닝(2)' 카테고리의 다른 글
| [밑시딥] seq2seq를 더 강력하게, 어텐션(Attention)을 적용한 seq2seq (3) | 2021.12.30 |
|---|---|
| [밑시딥] RNN을 사용한 문장 생성, 그리고 RNN을 이어 붙인 seq2seq(Encoder-Decoder) (0) | 2021.12.26 |
| [밑시딥] 게이트가 추가된 RNN, LSTM(Long-Short Term Memory) (2) | 2021.12.16 |
| [밑시딥] 과거의 기억을 그대로, 순환신경망(RNN) (4) | 2021.12.09 |
| [밑시딥] Embedding 계층과 Negative Sampling으로 효율적인 word2vec 구현하기 (2) | 2021.12.03 |



