이번 포스팅에서 다룰 내용들은 다음과 같다.
1. 정규분포의 정의
2. 이항분포에서 정규분포의 활용
3. 정규분포의 Error Function
4. 파스칼(Pascal)분포에 대한 간략한 개념
1. 정규분포의 정의
정규분포는 가우시안(Gaussian)분포라고도 부른다. 정규분포는 기본적으로 연속확률변수(Continuous)일 때를 다룬다. 그래서 정규분포의 확률변수는 연속확률변수이다. 그리고 정규분포는 이미지 센서, 오디오 음성 신호, 모바일 채널 등과 같은 case들에서 쓰인다. 또한 Quantization(양자화)과 같은 아날로그 데이터를 처리할 때도 가우시안 분포로 나타낼 수도 있지만 보통 연속균등분포(Uniform Dist)으로 나타낸다.

그렇다면 정규분포의 PDF(확률밀도함수), CDF(누적밀도함수)에 대해서 알아보자.

정규분포의 PDF, CDF정규분포의 PDF는 위 그림의 fx(x)식과 같다. 마찬가지로 정규분포 또한 PDF에서 적분과정을 통해 CDF로 나타낼 수 있다. 1번 초록색 동그라미의 그림을 보게 되면 우리가 고등학교 시절 배웠던 정규분포의 그림을 볼 수가 있다. 이 때 정규분포 모양의 특징들은 다음과 같다.
- Single-mode (그래프의 볼록하게 튀어나온 부분)
- Symmetric ( 대칭 그래프 )
- Bell-Shaped ( 종 모양의 그래프 )
1번과 2번 초록색 동그라미로 된 그래프들이 의미하는 바는 분산값이 크고 작으냐에 따라 실제값이 어떻게 분포되는지 알 수 있다는 것이다.
먼저 1번에서 빨간색으로 그려진 큰 분산은 2번 그림에서 빨간색 선으로 나타내어진다. y축의 값인 실제값이 위아래로 크게 변동치게 된다. 이는 결국 현실에서 음성을 들을 때 '지지직' 같은 노이즈가 껴있다거나 사진을 볼 때 선명하지 않을 때로 이어진다.
반면에 1번에서 파란색으로 그려진 작은 분산은 2번 그림에서 파란색 선으로 이어지고 실제값의 오차가 별로 없음을 의미하게 된다.
그리고 우리는 특정구간(x)까지의 CDF를 구함으로써 표준정규분포를 구할 수 있다. 위 식의 전개과정을 거쳐 N(0, 1)이 표준정규분포라는 것을 알 수 있다. 이렇게 표준정규분포로 바꿔주기 위해서 방법은 간단하다.
확률변수에 평균값을 빼주고 표준편차로 나누어 주면 된다.
간단한 예시를 통해서 표준정규분포로 바꾸는 방법을 적용해 보자.
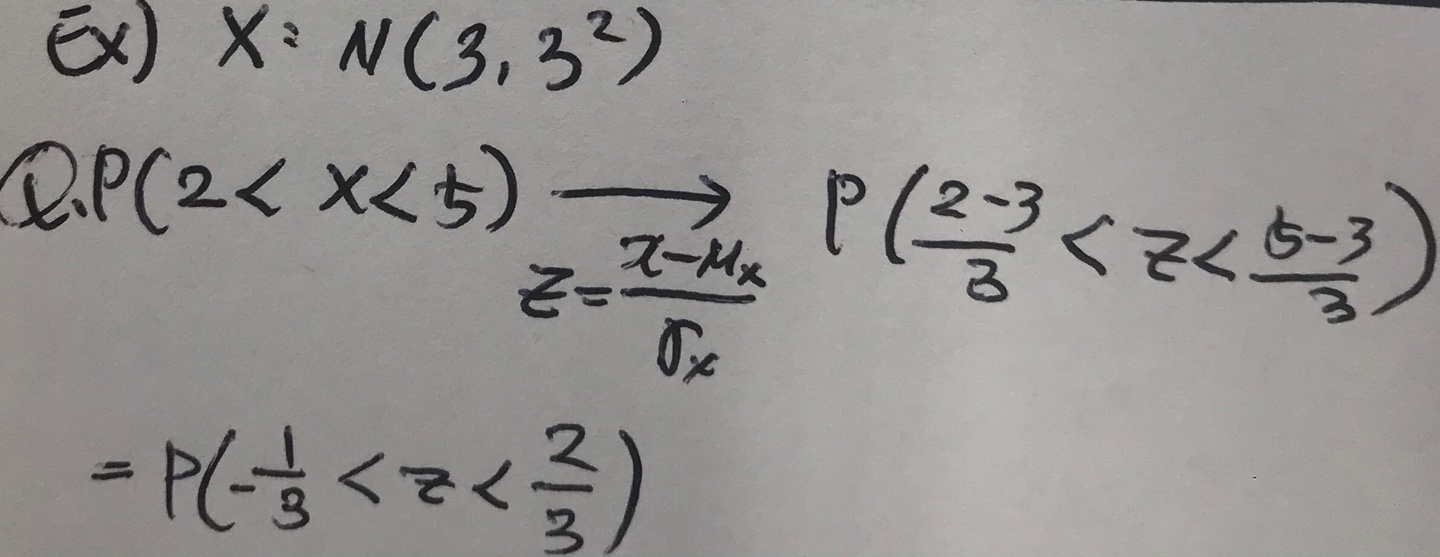
2. 이항분포에서 정규분포의 활용
이항분포는 베르누이 시행을 기반으로 한다. 따라서 a,b 특정 범위를 갖는 확률을 구해줄 때 시그마와 조합을 이용한 식으로 나타낼 수 있다. 하지만 이 조합을 일일이 계산하기가 어렵기 때문에 n이라는 시행횟수가 어느정도 크게 될 때 정규분포를 이용할 수 있다.

이항분포를 정규분포로 전환하면 N(np, np(1-p)) 값이 된다. 기본적으로 정규분포 N(평균, 분산값) 처럼 이항분포의 평균, 분산값을 구하는 공식을 적용해서 똑같이 해준다. 따라서 특정 a,b 구간의 확률을 정규화로 표현해본다면 위와 같은 식이 될 것이다.
이에 대해 그래프를 그려본다면 검은색 그래프 -> 파란색 -> 빨간색 으로 진행하면서(n=시행횟수가 커질수록) 대칭적인 그래프로 바뀌게 된다.
3. 정규분포의 Error Function
우리가 표준정규분포를 N(0, 1의제곱)이라고 정의해놓으면서 look-up table(적어놓고 필요할 때 들여다보는 테이블, cheat sheet같은 개념)로 이용을 한다. 또 다른 look-up table로서 Error Function이 있다.
Error Function은 보통 통신 분야에서 자주등장하는 독특한 모형이라 사람들이 따로 look-up table로 정리를 해놓은 것이다. 해당 함수의 식은 다음과 같다.
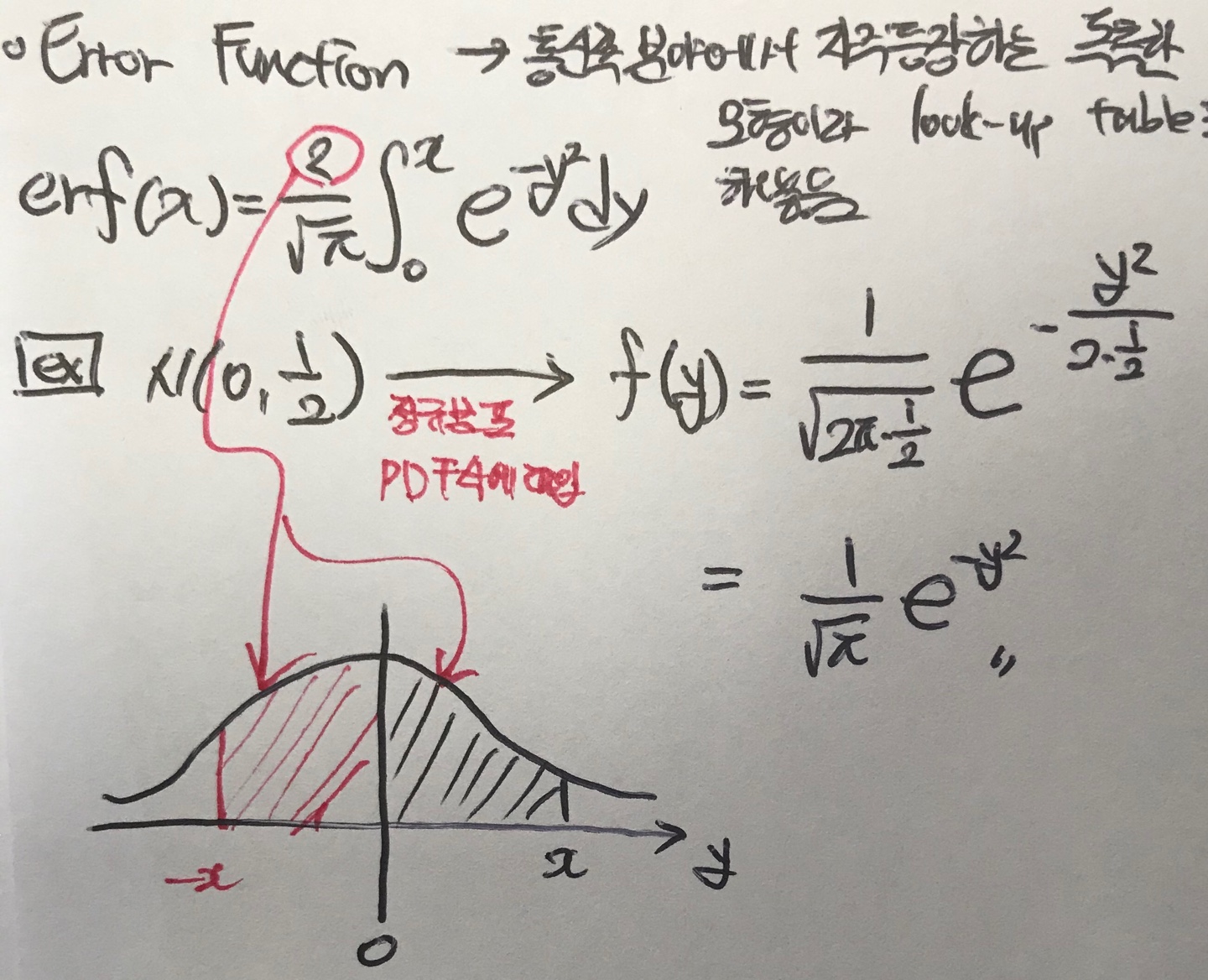
예를 들어 평균이 0 이고 분산이 1/2일 때 정규분포 PDF식에 대입을 해보자. 계산을 하면 f(y)같은 식이 나오게 되는데 이 때 f(y)와 f(x)의 식을 비교해면 2*f(y) = f(x) 가 된다. 이에 대한 이해를 하기 위해서 그래프 그림을 보고 이해해 보자.
또 하나의 Error Function으로 Complementary Error Function이 있는데 이에 대한 의미는 식보다는 그림으로 이해하는 것이 빠를 것이다. 밑의 그림 속 그래프를 보면 파란색으로 된 erf(x)는 우리가 방금까지 소개했던 f(y)가 되는 것이다.
그리고 지금 소개하는 Complementary Error Function이 빨간색으로 된 erfc(x)가 된다. 즉, 두개가 나타내는 구간이 다른 것이다. 따라서 이 두개의 함수를 각각 2씩 곱해줘서 합쳐준다면 전체 확률의 값인 1이 된다. 왜? 정규분포라 그래프 모양이 대칭이기 때문이다!
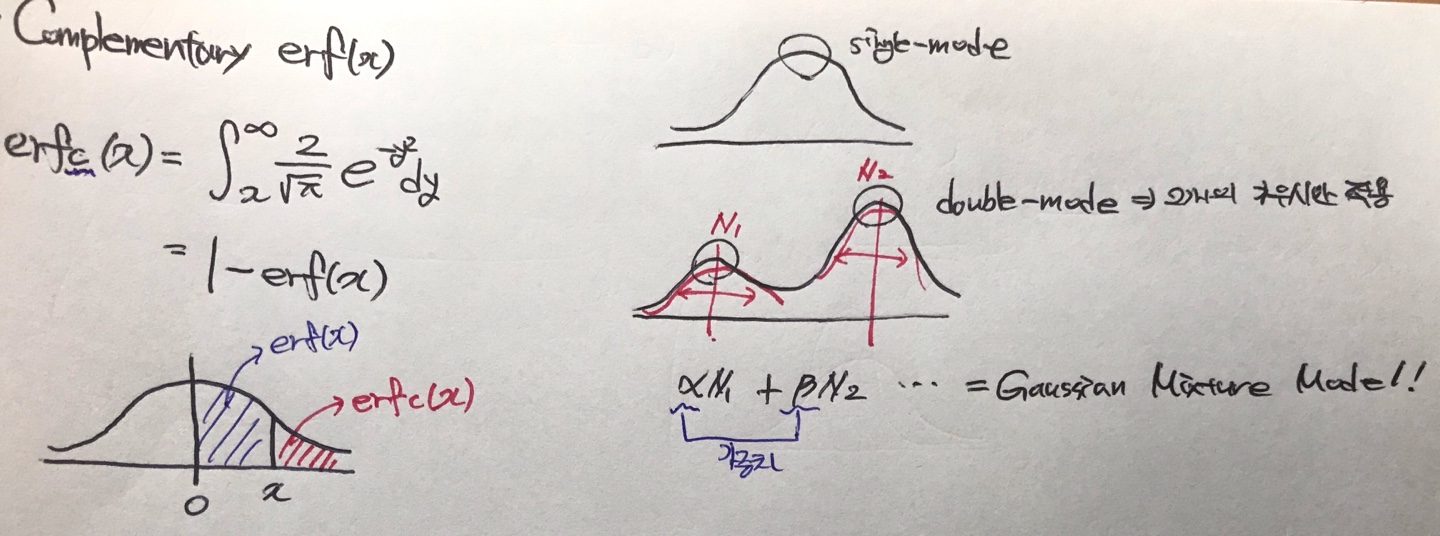
그리고 한 가지 더 설명할 것은 아까 정규분포의 특성 중 하나인 Single-mode에 대해 얘기해보려 한다. 여기서 mode란, 그래프의 볼록 튀어나온 부분을 일컫는데, 이 mode가 두개, 세개가 될 경우도 있다.
이 때는 우리가 mode를 기준으로 하여 평균값과 분산값을 구하고 각 mode 마다 정규분포를 구해준다. 그리고 각 정규분포에 그림 속의 알파나 베타값 처럼 가중치를 곱해주어 모두 합해준다. 이러한 Multi-mode를 Gaussian Mixture Model 이라고 부르며 GMM이라고 줄여 말하기도 한다.
4. 파스칼분포에 대한 간략한 개념
파스칼 분포는 기본적으로 기하분포(Geometric Dist)의 일반화된 버전이다. 들어가기전에 파스칼 분포의 확률변수에 대해서만 간단히 알아보려고 한다. 평균과 분산값은 수학적으로 너무 복잡하기에 해당 강의에서는 다루지 않았다.
(나중에 지적 호기심으로 찾아보는 걸로...)
파스칼 분포의 확률변수는 k번 성공할 때까지 베르누이 시행을 총 몇번 했는지에 대한 것이다. 이 때 k=1을 대입하게 되면 우리가 기존에 알고 있던 기하분포로 정의가 된다. 이해가 잘 안될 수도 있기에 그림으로 나타내 보았다.
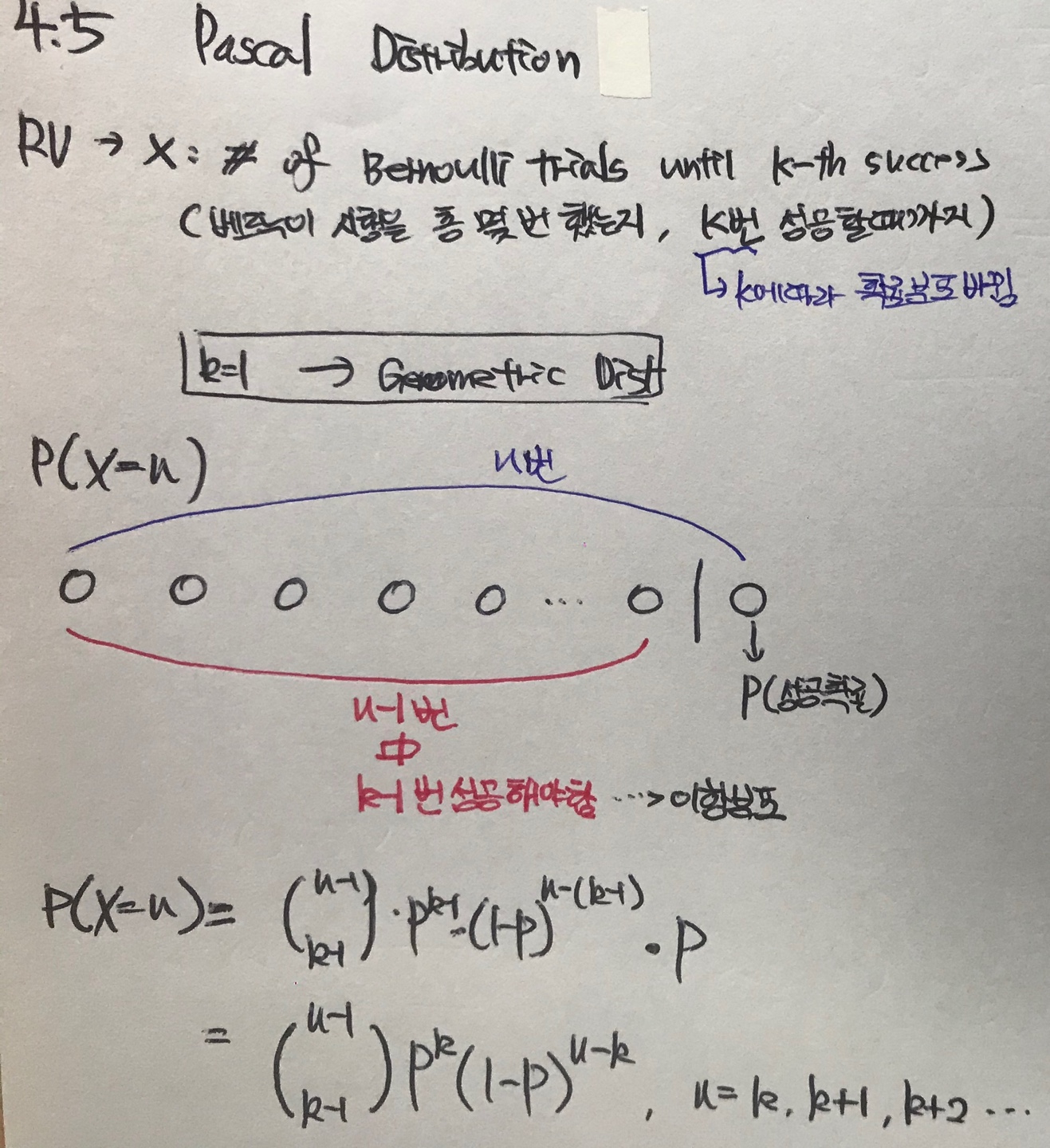
그림을 보면, n번 중 k번째에 무조건 성공해야 하고 그렇다면 n-1번중에서 k-1번 성공을 해야한다. 따라서 n-1번 중 k-1번 성공해야하는 확률을 이항분포로 정의할 수 있게 된다.
따라서 P(X=n)이라는 확률을 구하기 위해서는 그림과 같이 조합과 이항분포의 식을 이용해서 정의할 수 있다.
사실 파스칼 분포에 대한 설명을 들을 때는 정말 어렵다는 생각이 들긴 했다.. 확실히 수학적으로 복잡하기도 하며 n과 k라는 변수가 동시에 등장하다 보니 헷갈리기 시작했다. 파스칼 분포에 대해서는 좀 더 공부량이 필요할 것 같다.
'Data Science > 확률 및 통계' 카테고리의 다른 글
| 연합확률밀도함수와 조건부 확률밀도함수 (0) | 2020.03.23 |
|---|---|
| 다중변수(Multiple RV)와 연합분포 (0) | 2020.03.22 |
| 지수분포(Exponential)와 어랑분포(Erlang) (0) | 2020.03.20 |
| 베르누이분포와 이항분포의관계 그리고 체비쇼프 부등식 (0) | 2020.03.19 |
| 기하분포, 평균과 분산의 활용(Error Model) 그리고 조건부평균 (0) | 2020.03.18 |



