🔊 해당 포스팅은 밑바닥부터 시작하는 딥러닝 1권의 교재 내용을 기반으로 딥러닝 신경망을 Tensorflow, Pytorch와 같은 딥러닝 프레임워크를 사용하지 않고 순수한 Numpy로 구현하면서 딥러닝의 기초를 탄탄히 하고자 하는 목적 하에 게시되는 포스팅입니다. 내용은 주로 필자가 중요하다고 생각되는 내용 위주로 작성되었음을 알려드립니다.

이번 포스팅에서는 신경망 학습과 관련된 기술로서 파라미터를 갱신하는 최적화 기법, 파라미터 초기화 기법, 활성화 값들을 정규화시키는 배치 정규화 등의 방법들에 대해 이해해보고 넘파이로 구현해보려고 한다.
A. 최적화 기법
저번 포스팅까지 우리는 오차역전파를 통해 파라미터의 기울기(변화량들)를 구하는 방법에 대해 알아보고 이를 넘파이로 구현하는 것까지 배워 보았다. 그런데 기울기를 구한 후 파라미터를 갱신시킬 때는 지금까지 항상 SGD(Stochastic Gradient Descent)라고 불리는 확률적 경사 하강법을 활용해왔다.
참고로 Stochastic이라는 단어가 붙은 이유는 보통 신경망 학습 시 Mini-batch로 전체 데이터 중 일부를 추출해서 그 데이터들을 기반으로 기울기를 구한 후 파라미터를 갱신해주었기 때문이다. 그래서 일부 데이터가 전체 데이터를 대표한다는 의미에서 Stochastic(확률적)이라는 용어가 붙는다.
어쨌거나 오차역전파를 통해 얻은 기울기 즉, 손실함수 값을 가장 작은 값인 0으로 만들도록하는 파라미터의 변화량을 구했다. SGD와 같은 최적화 알고리즘의 목적은 다음과 같다. 이 변화량을 가지고 어떻게 파라미터를 갱신시켜줄 것인지가 바로 SGD와 같은 최적화 알고리즘의 목적이다. 비유를 하자면 오차역전파를 통해 얻은 기울기는 일종의 '지도' 역할이고 SGD와 같은 최적화 알고리즘은 그 '지도'를 가지고 '어떻게 탐험해 나갈지'를 의미한다고 볼 수 있다.
1. SGD(확률적 경사 하강법)
먼저 SGD의 수식에 대해서 살펴보자. 저번 포스팅에서 여러번 다루어 보았으니 수식에 대한 설명은 생략하겠다.
$$W_{new} = W_{old} - \eta {\partial L\over\partial W}$$
넘파이로 구현한 SGD 클래스는 아래와 같다. 아래의 params, grads 인자는 딕셔너리 형태로 저번 포스팅에서 오차역전파를 통해 신경망을 구현하는 코드에 대해 배울 때 사용했던 변수와 동일하다.
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params: dict, grads: dict):
for key in params.keys():
params[key] -= self.lr * grads[key]
그런데 SGD의 단점은 그럼 무엇일까? 결론부터 말하면, 손실함수가 어떻게 생겼느냐에 따라 SGD 기법이 비효율적이게 될 수 있다. 예를 들어, 다음과 같은 손실함수가 있고 우리는 이 $f(x, y)$ 값을 0이 되도록 하는 파라미터를 찾아야 한다고 가정하자.
$$f(x, y) = \frac{1}{20}x^2 + y^2$$
위 그래프 모양을 나타내면 아래와 같다.

위와 같은 함수를 미분하게 되면 기울기 그래프가 다음과 같이 그려진다.

기울기 그래프를 보면 대부분의 화살표가 $x$, $y$ 모두 0인 곳을 가리켜야 하는데, 그렇지 못한 모습을 보여준다. 이렇게 SGD를 활용해서 손실함수 값이 0이되는 곳을 찾아가는 경로를 시각화해보면 아래와 같이 된다.

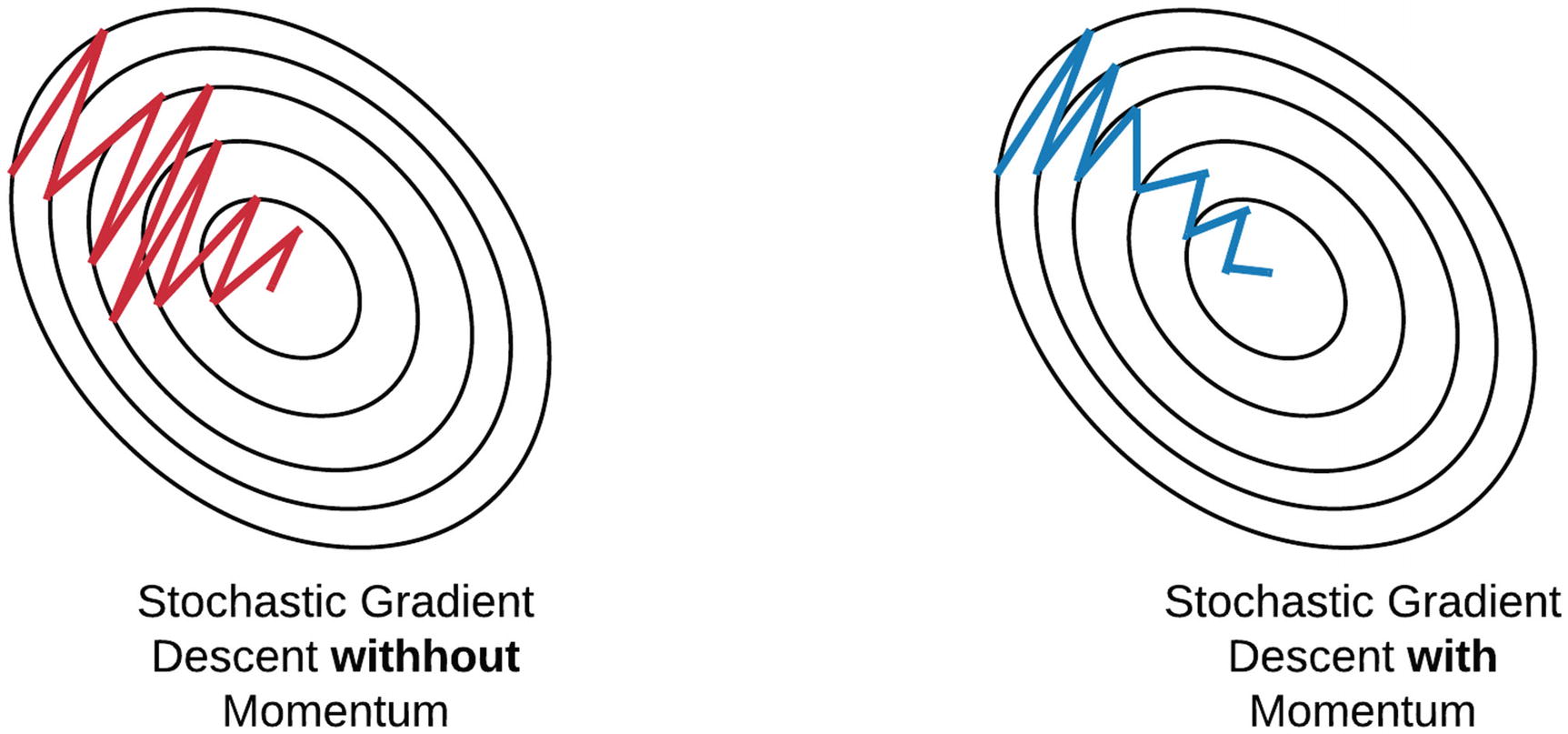
위 그림처럼 SGD는 위 아래로 매우 심하게 굽이진 움직임을 보여준다. 이러한 SGD의 단점을 비등방성(anistropy) 이라고도 하는데, 이는 기울기가 매번 달라지는 함수에서는 탐색 경로가 비효율적이라는 것을 의미한다. 또한 SGD가 지그재그로 탐색하는 원인 중 하나는 기울어진 방향이 찾으려는 최솟값과 다른 방향을 가리키기 때문에, 예를 들면, 기울기 값이 음수 값으로 나왔다면 양의 방향으로 파라미터를 갱신하기 때문에 기울기 값이 양수로 바뀌고, 다시 약간 음의 방향으로 이동하려면 기울기 값이 음수로 바뀜에 따라 계속 왔다갔다 수행하면서 지그재그 형태를 이루게 된다.
2. Momentum
모멘텀은 '운동량'을 의미하는데 물리 분야에서 유래한 개념이라고 한다. 모멘텀은 기울기(Gradient)를 보정하는 최적화 기법인데, $v$라는 새로운 변수('속도'라고 한다고 함)를 정의하여 파라미터 갱신하는 수식을 정의한다.
$$ v = \alpha v - \eta {\partial L\over\partial W}$$
$$W_{new} = W_{old} + v $$
위 수식에서 $\eta$는 학습률, ${\partial L\over\partial W}$은 손실함수에 대한 기울기를 의미한다. 이 때, $v$라는 ${\partial L\over\partial W}$와 동일한 shape의 행렬을 정의해주고 여기에 $\alpha$라는 값을 곱해준 후 이를 활용해서 기울기($\eta{\partial L\over\partial W}$)값을 보정해준다. 보통 $\alpha$은 0.9로 설정한다. 모멘텀을 사용하게 되면 SGD와는 다르게 지그재그하는 정도가 덜한 것을 볼 수 있다.
모멘텀을 넘파이로 구현한 코드는 아래와 같다.
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params: dict, grads: dict):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = (self.momentum * self.v[key]) - (self.lr * grads[key])
params[key] += self.v[key]3. AdaGrad
다음은 기울기가 아닌 학습률을 조정하는 AdaGrad 방식이다. AdaGrad는 학습률 감소(Learning rate Decay)라는 기술을 사용하는데, 학습을 진행하면서 점차 학습률을 줄여나가는 방식을 의미한다. 즉, 처음에는 큰 학습률로 학습하다가 점차 조금씩 작은 학습률로 학습한다는 의미이다. 그런데 보통은 모든 파라미터에 대한 학습률을 동시에 낮추는 게 방법이겠지만 AdaGrad는 이 방법에서 더 발전된 '각 파라미터에 맞게 학습률을 줄여나가는 방식'을 채택한다. 개별 파라미터에 '적응적으로(Adaptive)' 학습률을 조정한다는 것!
AdaGrad의 수식은 아래와 같다. 주목할 점은 $h$라는 새로운 변수인데 $h$라는 변수가 어디 곱해지는지 살펴보면 학습률을 의미하는 $\eta$옆에 곱해지는 것을 볼 수 있다.
$$h = h + {\partial L\over\partial W} \odot {\partial L\over\partial W}$$
$$W = W - \eta \frac{1}{\sqrt{h}}{\partial L\over\partial W}$$
위 수식에서 $\odot$은 행렬 원소별 곱을 의미한다. 즉, 위 수식에서 파라미터에 대한 손실함수의 기울기인 ${\partial L\over\partial W}$을 제곱하라는 의미이다. $h$를 보면 이 기울기값을 계속 제곱해나가는데 ,이를 파라미터 갱신 시에는 $\frac{1}{\sqrt{h}}$로 나누어주는 것을 볼 수 있다. 이것이 의미하는 바는 다음과 같다.
예를 들어, 어떤 파라미터 $W_k$가 엄청난 변화를 해서 기울기 값이 매우 크게 나왔다. 그러면 이때의 $h_k$값은 매우 클 것이다. 그러면 파라미터를 갱신해줄 때, 이 $h_k$값의 역수(정확히는 제곱근 후 역수지만)를 곱해줌으로써 큰 기울기 값인 $h_k$를 작게 만들어주게 된다. 그리고 이렇게 작아진 값을 학습률인 $\eta$에 곱해주게 된다. 결국, 파라미터 값들 중에서 이전에 크게 변화한 파라미터들은 이번에 갱신해줄 때 학습률을 낮추어서 갱신해준다는 것을 의미한다.
그런데 위 수식을 보면 기울기 값인 ${\partial L\over\partial W}$을 계속해서 제곱해나가는 것을 볼 수 있다. 이렇게 되면 학습이 진행됨에 따라 기울기 값은 0이 되게 되고 결국 파라미터는 갱신되지 않게 된다. 이를 개선한 방법으로 RMSProp 방법이 있다. 책에서는 자세하게 소개하진 않았지만, RMSProp은 매번 모든 기울기에 대해 균일하게 제곱을 해주는 AdaGrad와는 달리 과거의 먼 기울기일수록 즉, 학습한지 오래된 기울기 일수록 작은 가중치를 부여하고 최근의 기울기에 큰 가중치를 부여하는 '지수 이동평균' 방식을 AdaGrad에 적용한 것이라고 보면 된다. 그래서 과거의 기울기 반영 규모를 기하급수적으로 줄일 수 있게 된다.
AdaGrad와 RMSProp을 넘파이로 구현하는 코드는 다음과 같다. 참고로 아래에서 $\frac{1}{\sqrt{h}}$를 곱해줄 때 1e-7 이라는 매우 작은 수를 더해주는데, 이는 0으로 나누는 사태를 방지하기 위함이다. 딥러닝 프레임워크에서는 이 매우 작은 값을 인수로 설정할 수 있도록 했다.(주로 인자 이름이 epsilon이다)
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params: dict, grads: dict):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= (self.lr * grads[key]) / (np.sqrt(self.h[key]) + 1e-7)
class RMSProp:
def __init__(self, lr=0.01, rho=0.9):
self.lr = lr
self.rho = rho
self.h = None
def update(self, params: dict, grads: dict):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] = rho * self.h[key] + (1 - rho) * (grads[key] * grads[key])
params[key] -= (self.lr * sgrads[key]) / (np.sqrt(self.h[key]) + 1e-7)4. Adam
다음은 Adam 최적화 기법인데, 책에서도 이론적인 면에서는 자세히 다루지 않는다. 완전히 정확하지는 않지만 모멘텀과 AdaGrad를 합친 방법이라고 한다. 두 개를 합쳤다는 것은 기울기(Gradient) 보정과 학습률 조정 기술이 들어갔다는 것이다. Adam에는 추가적으로 편향 보정(Bias Correction)이라는 항도 추가되어 있다고 한다. Adam을 구현하는 넘파이 소스코드는 여기를 참고하자.
B. 가중치의 초깃값
신경망 학습에서 가장 중요하게 설정해야 하는 것 중 하나가 바로 가중치의 초깃값 설정이다. 초깃값을 무엇으로 설정하냐에 따라 신경망 학습 성공의 당락이 결정되기도 한다. 왜냐하면 신경망 학습의 목적은 가중치의 최적값을 찾는 것인데, 가중치 초깃값을 잘못 설정한다는 것은 시작부터 꼬인다는 의미이기 때문이다.
1. 초깃값을 0으로?
초깃값을 0으로 설정한다는 아이디어는 오버피팅을 억제하기 위한 방법으로 가중치 감소(Weight Decay)를 적용함으로써 인위적으로 가중치의 값을 작게 만드는 것에서 출발했다. 마치 가중치 값을 작게 만들려면 애초에 초깃값부터 작게 시작하면 되잖아? 같은 느낌이다.
하지만 가중치 초깃값을 모두 0으로 설정(또는 가중치 초깃값을 모두 동일한 값으로 설정)하게 되면 오차역전파를 수행할 때 문제가 발생한다. 왜냐하면 오차역전파를 수행하면서 파라미터의 변화량을 계산해서 파라미터를 갱신해주어야 하는데, 파라미터가 모두 동일하다면 변화량 또한 동일하게 나올 것이고 이는 파라미터 값이 똑같은 값으로 갱신되기 때문이다. 따라서 이러한 문제로 가중치의 초깃값은 무작위로 설정해주어야 한다.
2. 은닉층의 활성화값들 분포 형태를 보고 단서를 파악하자
초깃값을 무작위로 설정하긴 하는데 그러면 어떻게 무작위로 설정하라는 것인가? 그냥 랜덤하게? 매우 막연하다. 물론 훌륭한 연구자 분들이 이미 내놓은 무작위로 초기화하는 기법들이 존재하긴 하지만 이러한 기법들이 어떤 특징이 있길래 잘 먹히는(?)걸까?
그 해답은 은닉층의 활성화값들의 분포 형태에 있다. 우선은 아래의 소스코드를 활용해서 가중치 초깃값의 표준편차 값과 활성화 함수 종류에 따라 은닉층의 활성화값들 분포가 어떤 모양으로 그려지는지 살펴보자. 시각화하는 소스코드는 아래와 같다. 책 저자의 소스코드에서 약간 필자가 변형한 코드임을 밝힌다.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def relu(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
def visualize_hidden_outpus(weight_init_std=1, activation='sigmoid'):
input_data = np.random.randn(1000, 100) # 1000개의 데이터, 100개의 변수
node_num = 100
hidden_layer_size = 5
activations = {}
x = input_data
for i in range(hidden_layer_size):
# 첫 번째 층만 input_data 사용
if i != 0:
x = activations[i-1]
# 가중치 초깃값
if weight_init_std == 'xaiver':
w = np.random.randn(node_num, node_num) / np.sqrt(node_num)
elif weight_init_std == 'he':
w = np.random.randn(node_num, node_num) / np.sqrt(2 / node_num)
else:
w = np.random.randn(node_num, node_num) * weight_init_std # (1000, 100) x (100, 100) => (1000, 100)
# 행렬 곱
a = np.matmul(x, w)
# 활성함수
if activation == 'sigmoid':
z = sigmoid(a)
elif activation == 'relu':
z = relu(a)
elif activation == 'tanh':
z = tanh(a)
else:
return f'지정한 {activation}라는 활성함수는 함수 내에 설정되어 있지 않습니다'
# 은닉층 출력값 저장
activations[i] = z
# 히스토그램
for i, a in activations.items():
plt.subplot(1, len(activations), i+1) # size, nrows, ncols
plt.title(str(i+1) + "-layer")
if i != 0: plt.yticks([], []) # 첫번째 subplot 말고는 다 y축 삭제
plt.hist(a.flatten(), 30, range=(0, 1))
이제 표준편차값은 1, 활성화 함수는 sigmoid로 한 후의 은닉층 결과값들 분포를 히스토그램으로 살펴보자.
# 위 함수를 활용
visualize_hidden_outpus(weight_init_std=1, activation='sigmoid')
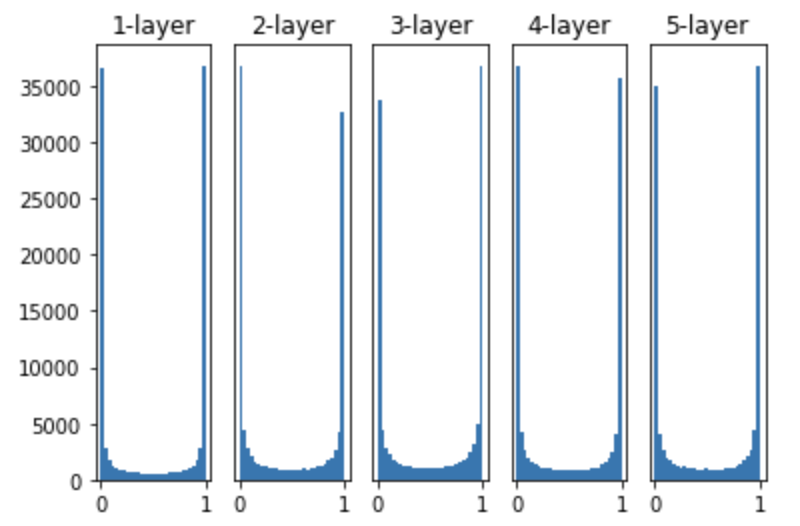
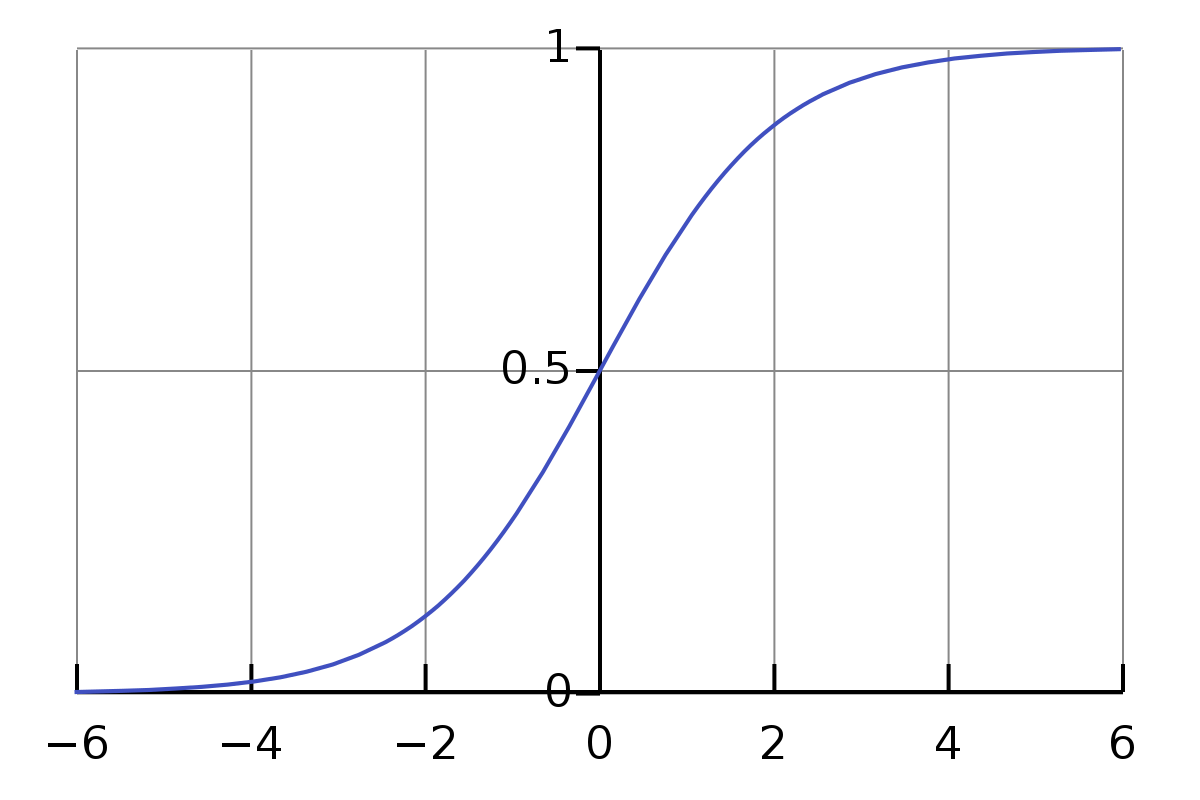
보다시피 5개의 은닉층의 출력값들 분포가 0아니면 1로 치우쳐여 있다. 그런데 방금 사용한 활성함수인 sigmoid 함수 그래프를 보면 출력값($y$값)이 0 또는 1에서 미분값이 0이 되버린다. 따라서 역전파를 수행하다가 기울기 값이 작아지다가 소실되는 Gradient Vanishing 문제가 발생한다.
그렇다면 활성함수는 동일시키되, 가중치 초기값의 표준편차 값을 0.01로 설정해보자. 표준편차가 0에 근사한다는 것은 결국 값의 종류 개수가 그만큼 매우 적다는 것을 의미하고 초기화된 가중치 값들이 거의 동일하다는 것을 의미한다.
# 위 함수를 사용
visualize_hidden_outpus(weight_init_std=0.01, activation='sigmoid')
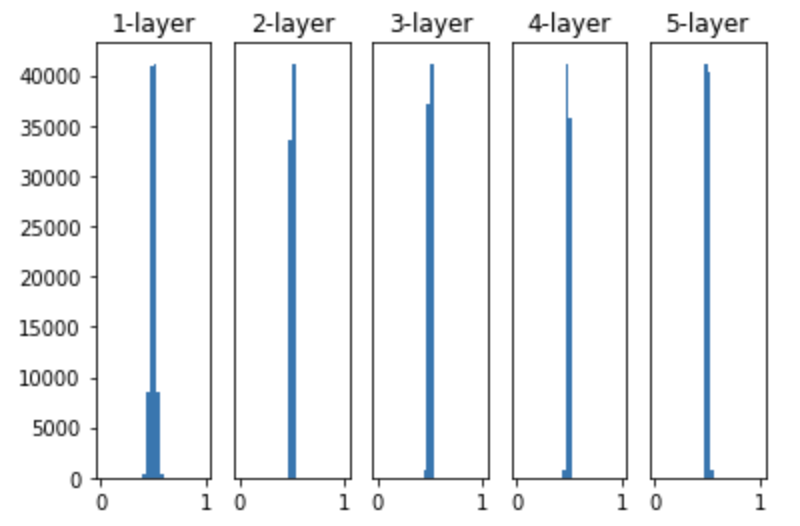
그래프를 보면 0과 1로 치우쳐져 있지는 않아서 기울기 소실 문제가 발생하지는 않는다. 하지만 5개의 신경망층에서의 출력값들이 모두 거의 동일한 값만을 출력하는 것을 볼 수 있다. 이렇게 되면 '표현력의 제한 문제' 가 있다고 책에서는 소개한다. 표현력의 제한 문제란, 출력값들이 모두 비슷한 값들로, 이렇게 되면 신경망 내부의 노드 개수를 여러개로 둔 이유가 없다는 것이다. 예를 들어, 노드 100개 모두 값 '1'을 가리키고 있다고 하자. 이렇게 되면 노드 1개가 값 '1'을 가리키는 것이랑 차이점이 없다는 것이다. 오히려 노드 100개로 늘어남으로써 계산 리소스만 낭비되고 있는 것이다.
그렇다면 은닉층의 결과값들 분포가 어떤 형태를 띄어야 신경망 학습이 잘될까? 뭐든지 '적당히'가 좋은 듯이.. 결과값들이 적당히 고루 분포되어 있어야 한다. 그래야 신경망 층 사이에 다양한 값들(데이터)이 흐름으로써 신경망 학습이 효율적으로 이루어지기 때문이다.
대표적인 방법들로는 신경망 층 간의 노드 개수를 고려해 가중치의 표준편차값을 설정하는 Xaiver 기법, Relu 활성함수도 고려한 He 초기화 기법이 존재한다. 이에 대해서는 이전에 다루었기 때문에 이론적인 부분은 여기를 참고하자. 두 기법의 핵심은 앞 계층의 노드가 많을수록 가중치의 표준편차 값을 작게하는 것이다.(표준편차를 작게 한다는 것은 곧 대부분의 가중치의 값들이 동일한 값이 되도록 분포시키는 것임을 기억하자)
이번 포스팅에서는 해당 기법들을 적용했을 때 은닉층들 결과값들 분포만 살펴보자. 먼저 Xaiver 초기화 기법과 sigmoid 함수를 적용했을 때이다.
# 위 함수를 사용
visualize_hidden_outpus(weight_init_std='xaiver', activation='sigmoid')
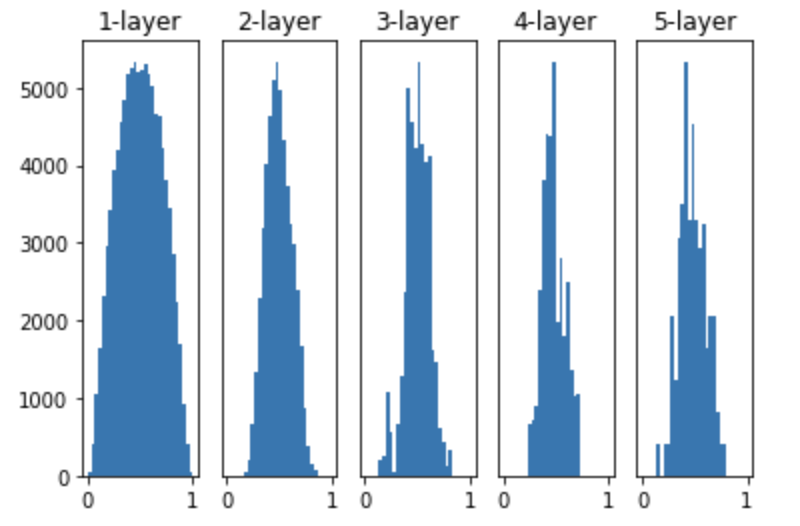
출력값들의 분포가 이전보다 훨씬 다양해진 것을 볼 수 있다. 층이 깊어질수록 분포가 변화하는 것을 볼 수 있다. 다음은 He 기법이다.
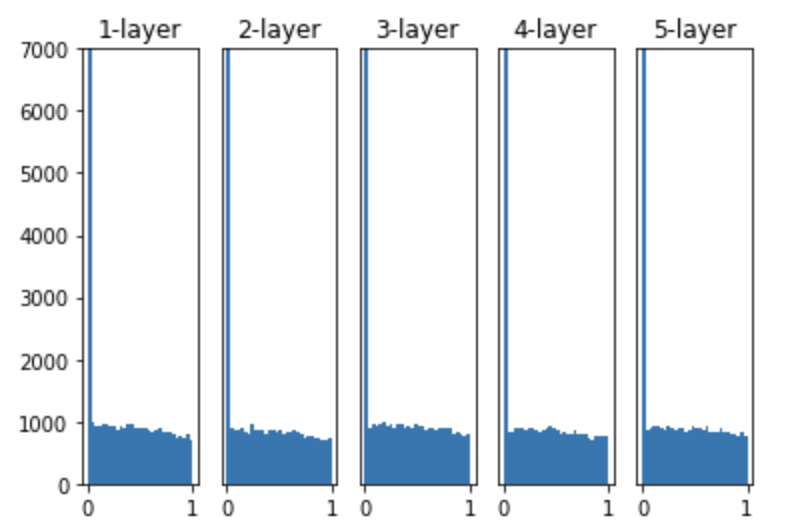
He 기법은 Relu 활성화 함수일 때 적절한 기법이기 때문에 Relu 함수을 사용했을 때 설정해주는 것이 좋다. 위처럼 출력값들의 분포가 고루 분포해 있는 것을 알 수 있다.
C. 배치 정규화(Batch Normalizaiton)
위에서 가중치 초기화를 적절히 설정하는 목적은 은닉층의 출력값들의 분포를 고르게 하기 위함이었다. 그렇다면 은닉층의 출력값들이 나왔을 때, 이 출력값들의 분포를 인위적으로 고르게 분포하도록 강제 변환해주면 어떨까? 그것이 바로 배치 정규화의 아이디어이다.
배치 정규화는 다음과 같이 3가지 특징을 갖고 있다. 먼저 학습을 빨리 진행시켜 학습 속도를 개선한다. 그리고 위에서 알아본 가중치 초깃값 설정에 의존하지 않는다. 마지막으로는 신경망의 오버피팅 문제를 예방할 수 있다. 또한 배치 정규화는 은닉층의 출력값에 활성함수를 씌우기 이전/이후에 적용할 수 있는데, 보통은 이전에 적용시켜야 학습 속도를 더 높일 수 있다고 한다.
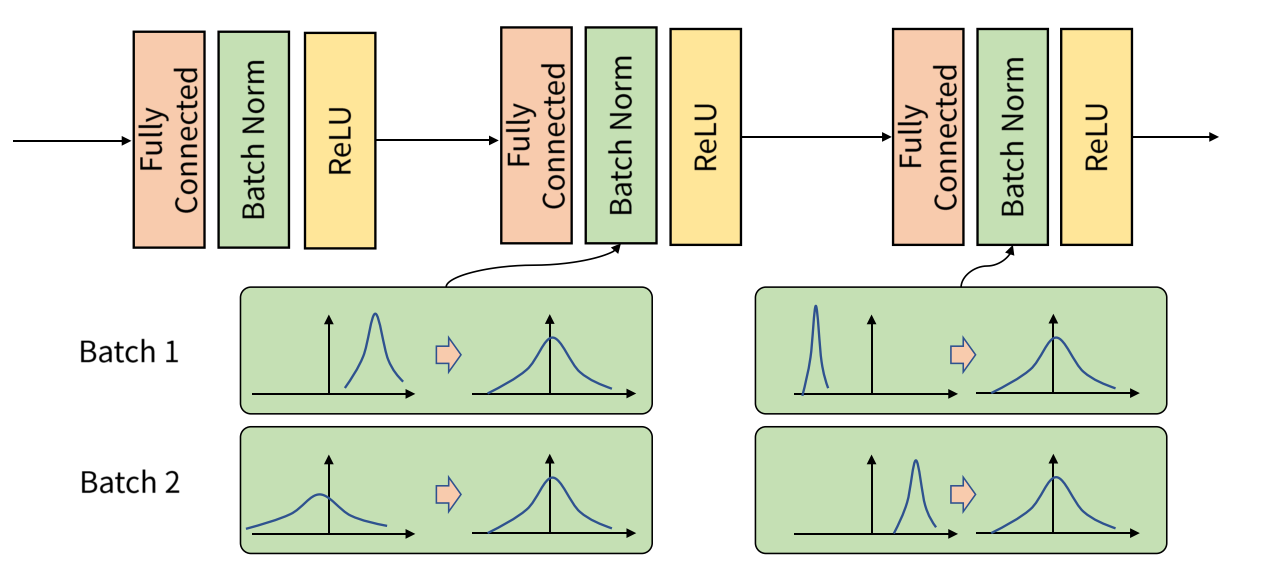
배치 정규화의 '배치'는 신경망 학습시 주로 사용하는 미니 배치의 그 '배치'랑 동일하다. 즉, 미니 배치로 들어오는 입력 데이터가 은닉층을 거쳐 나온 출력값들을 정규화시켜주는 것이 배치 정규화이다. 구체적으로는 출력값들의 평균이 0, 분산이 1이 되도록 정규화(Normlaization) 시켜주는 것인데, 그 수식은 아래와 같다.
$$\mu_B = \frac{1}{m} \sum_{i=1}^m x_i$$
$$\sigma_B = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2$$
$$\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma^2_{B} + \epsilon}}$$
$\mu_B$로 미니배치 데이터 $B$에 대한 평균값과 $\sigma_B$라는 분산값을 구해준다. 그리고 위 3번째 수식을 보면 정규화시켜줄 때 $\epsilon$이라는 값으로 0으로 나누어지는 상태를 방지한다.
그리고 배치 정규화는 이 정규화된 은닉층의 출력값들을 확대(scale)하고 이동(shift) 시키는 $\gamma$와 $\beta$ 라는 새로운 학습 파라미터를 추가해 $x$ 값을 아래처럼 재정의해준다.
$$y_i = \gamma\hat{x}_i + \beta$$
그런데 필자는 왜 확대와 이동시키는 파라미터를 추가해야 하는지 직관적으로 이해가 되지 않았다. 책에서도 명확한 이유를 밝혀주지 않아서 구글링해보았고 거의 이해가 가는 듯하 답변을 얻을 수 있었다. 원본 질문 링크는 여기를 참고하자.
위에서 살펴본 수식의 미지수들을 빌려보자면, 먼저 $\gamma$와 $\beta$ 라는 새로운 학습 파라미터를 추가하지 않고 단순히 은닉층의 출력값들을 정규화만 시켜준 $\hat{x}_i$는 어쨌거나 '정규화'라는 것을 적용했기 때문에 신경망의 표현력(Expressive power)을 제한시킨다. 아까 가중치 초깃값 목차에서 언급한 '표현력의 제한'이 이것과 동일한 의미이다. 즉, 출력값들을 정규화시켜준다는 것은 출력값의 종류를 대부분 비슷하게 만들어주게 된다. 이것은 곧 신경망의 표현력을 제한시키고 표현력을 제한시킨다는 것은 파라미터들이 모두 거의 비슷한 값으로 나오도록 한다는 것이다. 왜? 정규화를 시켜줌으로써 분산 값(구체적으로 표준편차 값)을 1로 만들어주었기 때문이다.
따라서 이러한 표현력 제한 문제를 해결하기 위해서 $\hat{x}_i$ 값에 확대와 이동이라는 파라미터인 $\gamma$와 $\beta$를 추가적으로 두어 $y_i$를 만들어준다. 이렇게 하는 이유는 기존의 정규화 값인 $\hat{x}_i$의 최적의 값은 신경망이라는 복잡한 작용 안에서 결정이 되지만, $\gamma$와 $\beta$를 추가적으로 두어 정의한 $y_i = \gamma\hat{x}_i + \beta$는 오로지 $\beta$ 값에 의해서 결정되기 때문이다.(마치 신경망과는 별개로 하나의 선형회귀식을 별도로 만든다는 느낌!) 그렇기에 $y_i $ 값의 최적화가 더 순조로워진다고 한다.
추가적인 학습 파라미터들인 $\gamma$는 1로, $\beta$ 는 0으로 초깃값이 설정되며 이는 1배로 확대(scale)하고 0 즉, 이동하지 않음(shift)을 뜻한다.
이렇게 배치 정규화는 출력값들을 정규화시킴으로써 학습 속도를 개선해준다. 뿐만 아니라 방금 알아본 $\gamma$와 $\beta$ 라는 추가적인 학습 파라미터가 들어갔다. 이는 결국 일종의 Noise 데이터가 들어간 것이기 때문에 이 $\gamma$와 $\beta$ 값들 때문에 일종의 정규화(Regularization) 효과가 발생해 어느정도 오버피팅 효과가 존재한다.(여기서 정규화는 Normalization이 아닌 Weight Decay의 정규화랑 동일한 의미이다)
하지만 배치 정규화는 오버피팅을 예방하기 위한 목적으로 쓰는 것보다 학습 속도를 개선시키고 출력값들의 분포를 다양하게 해주는 것이 주목적이다. 오버피팅은 배치 정규화를 쓰면서 얻는 부수적인 효과(?)일 뿐이다. 목적이 뒤바뀌면 안된다.
참고로 배치 정규화를 구현한 소스코드는 저자의 코드를 참고하자. 이를 구현하기 위해서 배치 정규화의 역전파 과정을 이해해야 하는데, 이는 따로 포스팅을 만들어 보려고 한다. 책에서 소개해주는 배치 정규화 역전파 과정을 계산 그래프로 설명한 블로그는 여기다.
D. 가중치 감소(Weight Decay)
Regularization이라고 하며, 한국어로는 정규화라고도 한다. 이 때 '정규화'라는 텍스트가 생긴 것은 동일하지만 값을 스케일링해주는 Normalization이랑 동일한 의미는 아니다. 헷갈리지 말자. 가중치 감소는 큰 가중치를 인위적으로 정규화 항을 부여하여 값을 감소시켜 오버피팅을 억제하는 역할을 한다. 크게 L2 노름, L1 노름 L 무한대 노름이 있는데, 이에 대해서는 예전 선형회귀 포스팅에서 다루었었다. 모른다면 해당 포스팅을 참고하자.
E. 드롭아웃(Dropout)
드롭아웃도 예전에 소개한 적이 있었다. 드롭아웃은 가중치 감소로는 오비피팅 억제에 한계가 있을 때 사용하는 방법인데, 신경망의 노드를 랜덤하게 삭제하는 방법이다. 단, 학습 시에만 노드를 삭제해 학습하고 테스트 데이터에 예측할 때는 노드를 삭제하지 않고 모든 노드를 사용해 예측한다. 구체적인 개념은 신경망을 개선시키는 여러가지 방법 포스팅을 참고하고 여기서는 넘파이로 구현하는 소스코드만 살펴보자.
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
# 학습 시
if train_flg:
self.mask = np.random.randn(*x.shape) > dropout_ratio
return x * self.mask
# 테스트 시에는 학습 때 삭제 안한 비율을 출력값에 곱해줌
return x * (1 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
위 소스코드의 forward() 함수인 순전파 함수에서 테스트일 때의 코드를 보자. 테스트 시에, 원래는 학습 시 삭제한 노드의 비율을 1에서 빼준 만큼 출력값에 곱해주어야 한다. 하지만 이는 꼭 필수적인 과정은 아니라고 한다. 그래서 딥러닝 프레임워크들도 테스트 시에 삭제한 노드의 비율을 1에서 빼서 곱해주지 않고 그냥 출력값만 전달하도록 구현되어 있다는 점도 알아두자.
지금까지 신경망 학습과 관련된 여러 기술들을 알아보았다. 공부해보면서 이전에 필자가 게시했던 포스팅 내용들과 많이 겹친다. 하지만 복습하기 위한 목적도 있으면서 빼먹을 내용 없이 모두 알아둬야 하는 지식이라고 생각되어서 반복해 기록한 이유도 있다.
'Data Science > 밑바닥부터시작하는딥러닝(1)' 카테고리의 다른 글
| [밑시딥] 오직! Numpy로 오차역전파를 사용한 신경망 학습 구현하기 (0) | 2021.11.14 |
|---|---|
| [밑시딥] 오직! Numpy와 계산 그래프를 활용해 활성화 함수 계층 오차역전파 이해하기 (0) | 2021.11.11 |
| [밑시딥] 오직! Numpy와 계산 그래프를 활용해 오차역전파 이해하기 (0) | 2021.11.10 |
| [밑시딥] 오직! Numpy와 수치 미분을 통해 신경망 학습시키기 (0) | 2021.11.06 |
| [밑시딥] 오직! Numpy로 간단한 신경망 구현하기 (0) | 2021.11.04 |



