🔊 해당 포스팅은 밑바닥부터 시작하는 딥러닝 1권의 교재 내용을 기반으로 딥러닝 신경망을 Tensorflow, Pytorch와 같은 딥러닝 프레임워크를 사용하지 않고 순수한 Numpy로 구현하면서 딥러닝의 기초를 탄탄히 하고자 하는 목적 하에 게시되는 포스팅입니다. 내용은 주로 필자가 중요하다고 생각되는 내용 위주로 작성되었음을 알려드립니다.

저번 시간까지 배웠던 Numpy로 신경망을 구성하는 방법과 이미 학습된 파라미터로 추론해보는 단계까지 해보았다. 이번 포스팅에서는 직접 넘파이로 설계한 신경망을 데이터를 통해 파라미터를 '학습'시키는 방법에 대해 알아보자.
먼저 학습시키는 방법을 알아보기 전에 손실함수라는 개념에 대해 알아야 한다. 손실함수는 일명 파라미터를 어떤 방향으로 학습시킬지 가이드라인을 제시해준다. 마치 우리가 등산할 때, 목적지가 어디에 있는지 중간중간 등장하는 표지판 같은 역할이라고 할 수 있겠다!
본격적으로 들어가기 전에 앞서서 우선 큰 그림을 통해 학습하는 과정을 이해해보자. 필자는 뭔가 이해가 되지 않거나 여러가지 과정이 얽히고 복잡해졌을 때, 항상 왜? 또는 어떻게? 질문을 던지는 경향이 있다. 이 방법을 사용해서 신경망 학습의 과정을 정리해보면 아래와 같다.

1. 손실 함수(Loss function)
손실함수를 배우기 전에 저번 포스팅에서 배운 활성화 함수랑은 헷갈리지 말자! 그리고 손실 함수를 Cost Function이라고도 부르기도 한다. 엄밀히 말해서 Loss와 Cost의 차이는 다음과 같다. 데이터가 100개가 있다고 할때, 1개의 데이터에 대한 손실 값은 Loss라고 하며 데이터가 여러개일 때의 손실 값을 Cost라고 한다. 물론 이 두 용어의 의미 차이가 신경망 학습에 물리적인 영향을 주진 않지만 워낙 동시에 사용되는 용어가 많기에 다른 분들과 협업하거나 소통할 때를 위해 참고로 알아둘 필요가 있다고 생각한다.
이제 대표적인 손실함수에 대해 알아보자. 첫 번째는 오차제곱합(Sum of Squares for Error, SSE)이다. 수식은 간단하다.
$$SSE = \frac{1}{2}\sum_{k}{(y_k-t_k)}^2$$
위 수식에서 $y_k$는 예측값을, $t_k$는 정답인 레이블을 의미한다. SSE를 코드로 구현하면 다음과 같다.
def sse(y, t):
loss = np.sum((y - t) ** 2)
return loss
# 정답에 근사했을 경우
y = np.array([0.1, 0.05, 0.6, 0., 0.05, 0.1, 0., 0.1, 0., 0,])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
loss = sse(y, t)
print(loss)
다음은 교차 엔트로피 오차(Cross-Enropy-Error, CEE)이다. 수식은 다음과 같다.
$$CEE = -\sum_{k}{t_k \log y_k}$$
이 때도, $y_k$는 예측값을, $t_k$는 레이블을 의미한다. 이 때, $t_k$는 정답인 인덱스 값만 1이고 나머지는 0인 2차원 배열의 원-핫 인코딩 형태이며, $y_k$도 2차원 배열의 Softmax 확률 값 형태이다. 교차 엔트로피 오차는 $t_k$가 0인 즉, 정답이 아닐 때는 계산하지 않고 정답인 1일 때만 옆의 자연로그를 계산하게 된다. 원래 로그함수는 단조 증가함수이지만 앞에 음수 기호를 붙여 반대로 단조 감소함수로 바꾸어 준다. 그럼으로써 결국 오른쪽 수식의 값이 작을수록 교차 엔트로피 오차는 작다는 것을 의미한다. 교차 엔트로피를 코드로 구현하면 아래와 같다.
def cross_entropy(y, t):
delta = 1e-7
loss = -np.sum(t * np.log(y + delta))
return loss
# 정답에 근사했을 경우
y = np.array([0.1, 0.05, 0.6, 0., 0.05, 0.1, 0., 0.1, 0., 0,])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
loss = cross_entropy(y, t)
print(loss)
그런데 위 코드에 delta 라는 매우 작은 수를 더해주었다. 이는 $\log 0$이 되버리면 마이너스 무한대로 발산해버리기 때문에 -inf 값이 나오게 된다. 따라서 매우 작은 수를 더해주어 소스코드로 구현한다는 점도 잊지말자.
방금 살펴본 CEE 수식은 데이터 1개에 대한 수식이다. 보통 신경망 학습할 때는 미니 배치를 통해 학습시킨다. 미니 배치를 사용할 때, CEE 수식은 아래와 같아진다. 단순히 미니 배치 데이터 개수인 $N$이 추가된 것 밖에 없다. $\frac{1}{N}$을 해주는 이유는 정규화(Normalization)해주기 위함이다.
$$CEE = -\frac{1}{N}\sum_{n} \sum_{k}{t_{nk} \log y_{nk}}$$
그렇다면 배치용 CEE를 소스코드로 구현하는 방법에 대해서 알아보자. 하단의 소스코드 2가지는 정답 레이블을 의미하는 $t_k$가 원-핫 인코딩 상태로 되어 있는지 아니면 단일 값으로 되어 있는 레이블 인코딩된 상태인지에 따라 다르게 구현해야 한다. 먼저 원-핫 인코딩된 상태로 레이블이 들어왔을 때 코드이다.
# 레이블이 원-핫 인코딩일 경우 CEE 손실함수
def cross_entropy_ohe(y, t):
# 데이터가 1개만 들어왔을 경우(1차원) -> 2차원으로 변환
if y.ndim == 1:
y = y.reshape(1, y.size)
t = t.reshape(1, t.size)
batch_size = y.shape[0]
loss = -np.sum(t * np.log(y + 1e-7)) / batch_size
return loss
다음은 레이블 인코딩되었을 때의 CEE 코드이다.
# 정답이 레이블 인코딩된 상태로 들어올 경우, CEE 함수
def cross_entropy(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
loss = -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
return loss
위 마지막 loss를 계산하는 부분에서 y[np.arange(batch_size), t] 부분을 이해하는 데 꽤 걸렸다.. 혹시 필자와 비슷한 상황인 사람이 있을 수도 있어 간단히 설명하자면, 여기서 np.arange(batch_size)는 예를 들어, batch_size가 10이라면 y[[0,1,2, ..., 9], t] 가 된다. 이 때 y는 현재 2차원 shape(데이터의 개수, 클래스 개수)으로 되어 있다. MNIST 데이터니까 손글씨 클래스는 0부터 9까지 10개이기 때문에 shape가 (10,10)이 될 것이다. 그렇기 때문에 y[[0,1,2,...,0], t] 의 [0,1,2,...,9]라는 이 부분은 인덱싱 번호로 데이터 행 가져온다고 생각하면 된다. 그리고 t는 '정답'으로서 레이블 인코딩된 값인데, 이 레이블 인코딩된 값을 인덱스로 하는 y의 값을 의미한다. 왜냐하면 현재 y는 원-핫 인코딩된 형태처럼 softmax 확률값으로 된 배열을 갖고 있기 때문이다. 예를 들어, [0.12, 0.2, ..., 0.45] 이런식으로 말이다. 그래서 이 Softmax 예측값이 들어있는 배열의 t 번째 인덱스 값과 비교하게 되면 결국 정답인 t와 t일 때의 Softmax 확률값에 대한 CEE를 계산할 수 있게 된다.
지금까지 손실함수 2가지에 대해 알아보았다. 그런데 왜 굳이 손실함수를 사용할까? 정확도와 같은 지표를 사용해서 파라미터가 학습할 방향을 설정할 수도 있지 않을까? 물론 정확도라는 지표로 세울 수도 있다. 결론부터 말하면 정확도라는 지표는 불연속적인 값을 내뱉는 경향이 강하기 때문에 적절하지 못하다. 이는 결국 미분이 하는 역할 때문에 정확도 지표를 사용하지 않는다고 볼 수 있다.
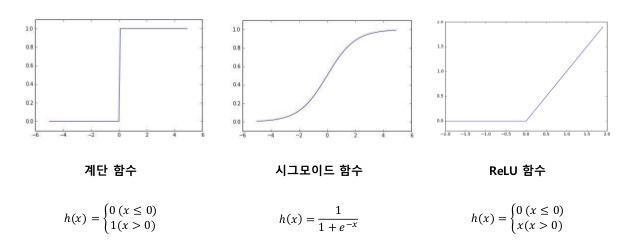
보통은 손실함수를 미분해서 계산해낸 변화량을 기반으로 가중치와 편향 값을 약간씩 조정하게 된다. 그런데 만약 이 때, 손실함수가 아닌 정확도를 계산하는 함수를 미분하면 어떻게 될까? 우선 정확도를 계산하는 함수는 마치 결과값을 이산적인 값들만 내뱉는 계단 함수처럼 생기게 될 것이다. 그렇다면 이런 함수를 미분하게 되면 대부분의 장소에서 변화량 값이 0이 되고 결국 가중치와 편향 값을 갱신하려 해도 변화량이 0이기 때문에 갱신되지 않을 것이다. 이는 이전 포스팅에서 배웠던 활성함수로 이산적인 값들만 내뱉은 계단 함수를 사용하지 않고 연속적인 값들을 내뱉는 시그모이드, Relu와 같은 함수를 사용하는 것과 맥락을 같이한다.
어쨌거나 손실함수는 입력값을 받아 활성함수를 적용시킨 뒤 나오는 결과값($y$)를 기반으로 손실함수를 만들어 내는데, 만약 활성함수를 이산적인 값들만 내뱉게 되는 계단함수를 사용하게 되면 손실함수도 미분하기 적절한 모양으로 나오지 않을 것이 분명하다.
2. 수치미분
다음은 변화량 값을 계산하기 위해 활용되는 수치미분이다. 고등학교 수학 시절 우리가 1번이라도 봤을 법한 수식이다.
$${\operatorname{d}\!f(x)\over\operatorname{d}\!x} = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
위 수식은 $h$를 한없이 0에 가깝게 함으로써 결국 $x$의 작은 변화가 $f(x)$를 얼마나 '변화'시키는지를 의미한다. 위 수식을 소스코드로 구현 할때, 주의해야 할 점 2가지가 있다. 첫번째는 바로 $h$에 가능한 작은 값을 대입하기 위해서는 $10^{-4}$값을 넣는 것이 가장 적절하다고 한다. 만약 그보다 더 작은 값들로 설정하게 되면 반올림 오차로 인해 계산 결과에 오차가 생겨버린다.
그리고 두번째는 차분과 관련된 것이다. 위 수식에서 $f(x+h) - f(x)$라는 차분을 이용했는데, 이를 전방 차분이라고 한다. $x+h$가 $x$ 보다 미세하지만 어쨌건 더 큰 값이기 때문에 '전방'이라는 의미를 붙인다. 하지만 소스코드로 구현할 때는 $x$를 중심으로 둔다고 하여 중심(중앙) 차분을 수행해서 수치 미분을 수행해야 한다. 아래 수식과 소스코드를 보면 단번에 이해할 수 있다.
$${\operatorname{d}\!f(x)\over\operatorname{d}\!x} = \lim_{h \to 0}\frac{f(x+h)-f(x-h)}{2h}$$
# 수치미분 계산 공식을 중심(중앙) 차분으로 변형 -> h를 2번 이용!
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
즉, $h$ 값을 활용해서 $x+h$, $x-h$ 두개에 대한 차분을 활용한다는 것이다. 또 h를 어쨌건 2번 사용했으므로 분모로 나누어 줄때 $2h$로 나누어야 한다는 것도 잊지말자.
3. 편미분
수치미분은 1개의 변수에 대한 미분을 의미했다면 편미분은 변수가 2개 이상일 때의 미분을 의미한다. 우선 아래와 같은 함수가 있다고 가정하고 이를 소스코드로 구현하면 아래와 같다.
$$f(x_0, x_1) = x_0^{2} + x_1^{2}$$
# 1. 2차함수로 구성된 새로운 함수 정의
def function_2(x: np.array):
return np.sum(x ** 2)
위와 같이 2개의 변수 $x_0, x_1$로 되어있는 함수를 어떻게 편미분을 할까? 방법은 한 변수씩 미분을 차례대로 수행해주면 된다. 즉, 위 식에서는 $x_0$을 미분하기 위해서는 $x_1$을 고정시킨 채 $x_0$에 관해 편미분을 수행하는 것이다. 아래의 소스코드는 $x_1$을 4.0이라는 고정값으로 넣어준 후 $x_0$에 대한 편미분을 수행한 결과값이다.
# x0 기준으로 편미분 수행 = x1은 상수로 고정!
def square_func_temp1(x0):
y = x0*x0 + 4.0**2 # x1을 4.0으로 고정
return y
# x1을 상수로 고정시킨 후 x0가 3일 때 h만큼 늘리면 f 값은 얼마나 변화했는가? 를 의미
print(numerical_diff(square_func_temp1, 3.0))
위 print 문 주석에도 써있다 시피 헷갈리지 말자! 현재 우리는 위 수학 수식과 똑같은 함수를 정의하되 $x_1$을 4.0이라는 상수로 고정시키고 함수를 만들었다. 그리고 위에서 만들어준 수치 미분 계산 함수에 넣어준다. 미분 계산 함수에 넣어줄 때, $x_0$을 3.0으로 넣어주었을 때, y값이 얼마나 변화했는지를 의미한다.(numerical_diff가 반환하는 값이 y 결과값을 의미하는 것이 아님에 주의하자!)
이제 $x_0$을 상수로 고정시키고 $x_1$에 관해 편미분을 수행해보자. 과정을 위와 동일하다.
def square_func_temp2(x1):
y = 3.0**2 + x1*x1 # x0을 3.0으로 고정
return y
# x0을 3.0으로 고정시키고 함수에 x1에 4.0을 대입했을 때 결과값이 얼마나 변화하는가? 의미
print(numerical_diff(square_func_temp2, 4.0))4. 기울기
위에서 편미분을 배웠다. 방금은 두 개의 변수일 때, 편미분을 하나씩 계산해 주었다. 그러면 이를 동시에는 할 수 없을까? 이 때, 모든 변수의 편미분을 벡터(행렬)로 정리한 것을 바로 기울기(Gradient)라고 한다. 개인적으로 '변화량 = 기울기' 또는 '미분 = 기울기' 라는 애매한 등식을 생각하고 있었는데 약간은 잘못 알고 있었구나라는 생각이 들었다. 이들은 서로 약간 다른 개념이며 여러 변수들의 변화량들을 벡터로 모아놓은 것을 기울기라고 할 수 있다.
그런데 편미분을 동시에 한다고 하는 개념이 아직은 와닿지 않을 것이다. 이럴 때는 소스코드로 살펴보면 이해가 갈 것이다. 변화량을 행렬로 정리한 것이라고 했으니 우리는 매우 유용한 행렬 처리 라이브러리인 넘파이를 사용할 수 있다.
def function_2(x: np.array):
return np.sum(x ** 2)
def numerical_gradient(f, x: np.array):
h = 1e-4
# Gradient 담을 벡터행렬 초기화
grad = np.zeros_like(x)
# array의 원소 하나씩 편미분 수행(=하나의 변수씩 편미분 수행)
for idx in range(x.size):
temp_val = x[idx]
# f(x+h)
x[idx] = temp_val + h
fxh1 = f(x) # x라는 전체 array를 넣는 이유는 f 값을 계산하기 위해서는 모든 x들(변수들)이 필요하니까!
# f(x-h)
x[idx] = temp_val - h
fxh2 = f(x)
# 미분 공식 수행
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = temp_val # 다른 변수의 편미분 수행해주기 위해서 -h/+h 했던 원소값을 복원
return grad
print(numerical_gradient(function_2, np.array([3.0, 4.0])))
print(numerical_gradient(function_2, np.array([8.0, 10.0])))
print(numerical_gradient(function_2, np.array([-5.0, -3.0])))
필자가 이해하면서 작성한 주석를 최대한 상세히 작성했다.(혹시 이해가 안거거나 하면 답글을 달아주세요!) 위 코드를 수행해보면 어떤 기울기의 요소값(변화량)은 음수, 어떤 것은 양수로 나온다. 그러면 이 기울기의 값들이 의미하는 것이 무엇일까? 만약 기울기의 변화량 값이 음수라고 한다면 가중치, 편향 값들을 양의 방향으로 변화시켜야 손실함수의 값을 줄일 수 있음을 의미한다. 반대로 변화량 값이 양수라면 가중치, 편향 값들을 음의 방향으로 변화시켜야 손실함수의 값을 줄일 수 있음을 의미한다.
(이를 좀 쉽게 이해하기 위해서 우리가 지금껏 구한 변화량들은 일종의 '벡터'이다. 벡터의 세계에서는 양수/음수 부호는 있지만 그것이 대소비교를 할 수 있는 것이 아닌 단지 '방향'을 가리킴을 인지하고 있자!)
5. 경사하강법
다음은 위에서 구한 기울기로 각 가중치, 편향 값들을 갱신해주는 방법으로서 경사하강법에 대해 알아보자. 경사하강법을 한 마디로 정의한다면 '우리가 위에서 구한 기울기 값들이라는 것을 가이드로 삼아서 손실함수 값의 최솟값 또는 최댓값을 찾으려는 것' 이라고 할 수 있다. 하지만 기울기가 가리키는 방향으로 간다고 해서 무조건 손실함수 값을 최솟값 또는 최댓값으로간다는 보장은 없다. 이럴 때, 우리가 찾은 값이 극솟값(Local minimum)인지 최솟값(Global minimum)인지 모른다고 한다.
이제 위에서 배웠던 수치미분, 편미분, 기울기 구하는 방법을 활용해서 경사하강법을 통해 가중치, 편향 값을 갱신시켜보자. 이 때, 알아야 할 하이퍼파라미터는 학습률(Learning rate)이 있다. 학습률은 대부분 의미를 아실테지만 "파라미터 갱신 시 얼마만큼 갱신시켜야 할지"를 정하는 학습의 정도를 의미한다. 경사하강법 수식과 소스코드는 아래와 같다.(변수가 2개 일 때를 가정했다)
$$x_0 = x_0 - \alpha{\operatorname{d}\!f\over\operatorname{d}\!x_0}$$
$$x_1 = x_1 - \alpha{\operatorname{d}\!f\over\operatorname{d}\!x_1}$$
def function_2(x: np.array):
return np.sum(x**2)
def gradient_descent(f, init_x: np.array, lr=0.01, step_num=100):
x = init_x # 100번의 경사하강 수행
for _ in range(step_num):
# 1. (손실) 함수인 function_2 기반으로 기울기를 반복 계산
grad = numerical_gradient(f, x)
# 2. x값 업데이트
x -= lr * grad
return x
init_x = np.array([-3.0, 4.0])
print(gradient_descent(function_2, init_x, lr=0.1, step_num=100))6. 학습 알고리즘 구현하기
이제 지금까지 배운 것을 모두 종합해서 사용해볼 차례이다. 학습 알고리즘을 구현하기 위한 단계적 로직을 설명하면 아래와 같다.
- 가중치와 편향을 데이터에 맞게 초기화하고 신경망 구조를 설계
- 정의한 배치 사이즈만큼의 미니 배치 데이터 가져오기
- 배치 데이터만큼의 기울기 계산
- 가중치와 편향 갱신
- 1 ~ 3번을 정해진 횟수만큼 반복
클래스를 사용한 소스코드는 아래와 같다. 하단의 코드에서 import 해서 사용된 것들은 책의 저자가 직접 만든 코드로, 우리가 위에서 구현한 것들로 사용해도 되긴 하지만 대부분의 경우의 수를 고려해 완성된 저자의 소스코드를 임포트해서 사용하자. 해당 Github 링크는 여기를 참조하자.
# 학습 알고리즘 구현하기 -> 2층 신경망의 MNIST 데이터 학습
import numpy as np
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 파라미터 담을 딕셔너리
self.params = {}
self.params['W1'] = np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 예측 메소드
def predict(self, x):
w1, w2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
# Layer 1
a1 = np.matmul(x, w1) + b1
z1 = sigmoid(a1)
# Layer 2
a2 = np.matmul(z1, w2) + b2
y = softmax(a2)
return y
# 손실함수 메소드
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t) # 함수를 반환
# 정확도 측정 메소드
def accuracy(self, x, t):
""" t: One-hot-Encoding format(2-dim shape) """
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
acc = np.sum(y == t) / float(x.shape[0])
return acc
# 각 파라미터의 기울기(변화량) 계산 -> 손실함수를 낮추기 위한 가이드 구하는 셈!
def numerical_gradient(self, x, t):
# 1. 손실함수 계산
loss_func = lambda w: self.loss(x, t)
# 2. 각 파라미터에 대해 기울기 계산
grads = {}
grads['W1'] = numerical_gradient(loss_func, self.params['W1'])
grads['b1'] = numerical_gradient(loss_func, self.params['b1'])
grads['W2'] = numerical_gradient(loss_func, self.params['W2'])
grads['b2'] = numerical_gradient(loss_func, self.params['b2'])
return grads
위에서 정의한 클래스로 MNIST 데이터를 활용해 학습시켜보자. 학습 방식은 미니 배치 학습을 구현했다.
# 미니배치 학습 구현하기
import numpy as np from dataset.mnist import load_mnist
(X_train, y_train), (X_test, y_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss = []
# 하이퍼파라미터
iters_num = 10
train_size = X_train.shape[0]
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 미니 배치로 SGD 수행
for i in range(iters_num):
# 미니 배치 데이터 할당
batch_idx = np.random.choice(train_size, batch_size)
X_batch = X_train[batch_idx]
y_batch = y_train[batch_idx]
# 기울기 계산
grads = network.numerical_gradient(X_batch, y_batch)
# 기울기 계산한 것을 기반으로 파라미터 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grads[key]
# 파라미터 갱신 후의 Loss 값 측정
loss = network.loss(X_batch, y_batch)
train_loss.append(loss)밑바닥부터 시작하는 딥러닝 챕터 4에 대한 정리가 끝이났다. 위 코드를 실행해보면 아시겠지만 iters_num 숫자를 좀만 늘려도 시간이 엄청 오래 걸린다. 이는 결국 미분을 수행할 때, 수치 미분을 사용한다는 점 때문인데, 다음 챕터 5에서는 계산과정이 복잡하지만 속도가 상대적으로 빠르며 딥러닝의 꽃이라고 할 수 있는 오차역전파 방법에 대해서 알아보자.
'Data Science > 밑바닥부터시작하는딥러닝(1)' 카테고리의 다른 글
| [밑시딥] 오직! Numpy로 학습관련 기술들 구현하기 (0) | 2021.11.16 |
|---|---|
| [밑시딥] 오직! Numpy로 오차역전파를 사용한 신경망 학습 구현하기 (0) | 2021.11.14 |
| [밑시딥] 오직! Numpy와 계산 그래프를 활용해 활성화 함수 계층 오차역전파 이해하기 (0) | 2021.11.11 |
| [밑시딥] 오직! Numpy와 계산 그래프를 활용해 오차역전파 이해하기 (0) | 2021.11.10 |
| [밑시딥] 오직! Numpy로 간단한 신경망 구현하기 (0) | 2021.11.04 |



