이번 포스팅에서는 기존 여러 개의 변수의 차원의 축소를 수행해주면서 추출되는 새로운 변수를 만드는 즉, Feature extraction 중 한 가지 방법으로서 PCA(주성분 분석)에 대한 내용이다. PCA가 구체적으로 무엇이고 정의는 어떻게 되는지에 대해서는 기존 포스팅을 참고하자.

그래서 이번에 다룰 내용은 PCA를 수행할 때 '몇 개'의 변수로 차원을 축소할지 결정하는 기준에 대한 내용이다. 이 기준에 대해서 알아보기 위해 예시 데이터를 활용해서 적절한 주성분 개수를 설정해보자. 참고로 이번에 사용될 데이터는 종속변수가 없는 독립변수들 끼리만 활용해볼 것이다. 왜냐하면 이번 포스팅의 목적은 PCA를 통해 종속변수 예측력에 영향을 준다는 내용보다는 독립변수들에 PCA 수행을 해주었을 때 몇 개의 주성분으로 축소되야 적절한지 살펴보는 것이기 때문이다.
주성분 개수를 설정하는 기준에는 크게 3가지가 존재한다. 첫 번째는 고윳값(설명 가능한 분산), 두 번째는 누적 기여율, 마지막으로는 Scree plot을 통해 결정한다.
이번 포스팅에서 사용할 예시는 R에서 내장 데이터로 제공되는 heptathlon 데이터로 1988년 서울 올림픽 육상 여성 7종 경기에 대한 결과 데이터이다.
# 모든 변수가 독립변수이므로 모든 변수를 가지고 PCA 적용
data = pd.read_csv('trackrecord2005-men.txt', delim_whitespace=True)
print(data.shape)
data.head()

위와 같이 데이터를 미리보기 했을 때, index는 여러 국가이며 columns는 8개로, 각 육상 종목을 나타낸다. 우리는 우선 PCA를 수행해주기 전에 변수들의 단위를 표준화시켜주어야 한다. 즉, PCA 수행 시 상관행렬을 이용해 표준화계수로 만들어준 후 PCA를 수행해주자.
# 상관행렬을 이용하기 위한 표준화계수로 만들기 위해 scaling
from sklearn.preprocessing import StandardScaler
std_df = StandardScaler().fit_transform(data)
std_df = pd.DataFrame(std_df, index=data.index, columns=data.columns)
data = std_df
data.head()

그리고 이제 PCA를 수행하자. 적절한 주성분 개수를 설정하기 위해서 우선은 원본 데이터의 변수 개수(feature 개수)만큼의 개수로 설정해서 PCA를 수행한다. 그리고 각 주성분값들을 데이터로하는 데이터프레임을 생성하자.
# 모든 독립변수 개수(8개)만큼 주성분 개수 설정해서 분석하기
from sklearn.decomposition import PCA
pca = PCA(n_components=8)
pca_array = pca.fit_transform(data)
pca_df = pd.DataFrame(pca_array, index=data.index,
columns=[f"pca{num+1}" for num in range(data.shape[1])])
pca_df.head()

위와 같이 주성분을 8개로 설정했을 때 결과가 나왔다. 위 코드에서 PCA를 수행해준 변수 pca 라는 변수의 객체를 이용해 고윳값(설명가능한 분산값)과 누적 기여율을 만들어보자. 참고로 기여율을 계산하는 공식은 다음과 같다. 하지만 Scikit-learn의 PCA 메소드는 편리하게 공식을 직접 구현할 필요없이 'explained_variance_ratio_' 를 반환하면 쉽게 얻을 수 있다.

# 주성분의 설명력과 기여율 구하기
result = pd.DataFrame({'설명가능한 분산 비율(고윳값)':pca.explained_variance_,
'기여율':pca.explained_variance_ratio_},
index=np.array([f"pca{num+1}" for num in range(data.shape[1])]))
result['누적기여율'] = result['기여율'].cumsum()
result

위와 같이 각 주성분의 고윳값과 주성분 마다 기여율을 누적한 누적 기여율을 계산한 데이터 프레임이 완성되었다. 여기서 개별 고윳값 즉, 각 주성분 마다 고윳값이 0.7이상인 주성분들, 누적기여율이 80% 이상이 넘어거지는 지점까지의 주성분들을 기준으로 하여 적절한 주성분 개수를 설정한다.
위 데이터프레임에 기준을 적용한다면 pca1 즉, 제 1주성분의 고윳값이 6.829767, 누적기여율이 약 83%로. 제 1주성분만을 이용한다고 해도 적절한 주성분 개수 기준을 충족시킨다. 따라서 현재까지는 가장 적절한 주성분 개수는 제 1주성분, 1개로 PCA를 수행해주는 것이 좋다고 판단할 수 있다.
주성분 개수를 설정하는 마지막 판단 기준으로 Scree plot을 이용할 수 있다. Scree plot은 x축을 주성분 개수, y축을 고윳값(설명가능한 분산 값)으로 하는 line graph를 의미한다. 다음 코드를 이용해서 Scree plot을 그려보자.

위 line graph에서 line이 급작스럽게 완만해지는 지점인 빨간색 동그라미 부분이 바로 적절한 주성분 개수라고 볼 수 있다. 하지만 지금 이용하고 있는 예시 데이터에서는 그렇지 않지만 만약 다른 데이터에서 적절한 주성분 개수를 관찰하기 위해 Scree plot을 살펴보았을 때, 완만해지는 지점이 애매모호할 수 있다. 따라서 보통은 Scree plot 보다는 위에서 언급한 기준이었던 '고윳값', '누적 기여율'을 주로 이용한다.
이제 적절한 주성분 개수를 설정할 수 있게 되었다. 바로 제 1주성분 1개이다. 하지만 여기서 제 2주성분까지 2개의 주성분으로 축소한 후 x축은 제 1 주성분, y축은 제 2 주성분으로 하는 biplot 그래프를 그려본 후 PCA를 통해 추출된 변수인 제 1 주성분 즉, 모든 국가들의 이른바 '육상 종합점수'를 기반으로 어떤 국가들이 종합점수가 가장 높은지, 우리나라는 몇 위인지 살펴보자.(참고로 제 1 주성분을 '육상 종합점수'라고 네이밍하는 것은 데이터 분석가의 몫이므로 분석가에 따라 또는 차원 축소 전 변수의 도메인에 따라 네이밍하는 변수 이름이 달라질 수 있음을 알아두자.)
from sklearn.decomposition import PCA
from pca import pca # biplot을 그리기 위한 별도 라이브러리
import seaborn as sns
pca = PCA(n_components=2)
pca_array = pca.fit_transform(data)
pca_df = pd.DataFrame(pca_array, index=data.index,
columns=['pca1','pca2'])
model = pca(n_components=2)
results = model.fit_transform(data)
fig, ax = model.biplot(n_feat=2, legend=False)
제 1주성분을 x축, 제 2 주성분을 y축으로 하여 데이터를 좌표로 찍은 후 biplot을 그려보았다. 각 점은 데이터를 2차원 평면에 좌표를 찍어 나타낸 것이다.

위 그래프에서 x축 즉, PC1(제 1 주성분)을 기준으로 PC1 값이 큰 양수값일 수록 '종합 점수'가 높은 나라이다. 여기서 PC1 값이 양수 일수록 종합점수가 높은지, 음수 일수록 종합점수가 높은지는 PCA를 수행해준 후 도출된 고윳값이 양수/음수에 따라 판단하면 된다. 만약 제 1주성분과 같이 상위의 주성분의 고윳값들이 음수값들로 도출되었다면 위 그래프와는 달리 PC1 값이 음수에 가까울 수록 종합점수가 높다는 것을 의미한다. 왜냐하면 주성분의 고윳값은 벡터이기 때문이다. 벡터에서 음수/양수는 단순히 방향만을 의미한다.
또한 그래프의 빨간 선은 변수를 의미한다. 그래서 종합점수가 가장 높은 나라는 Cookislands라는 나라이다.
이번엔 8개의 주성분 모두를 이용해 biplot을 그려보자.
from pca import pca
model = pca(n_components=8)
results = model.fit_transform(data)
fig, ax = model.biplot(n_feat=8, legend=False)

위 그래프에서 빨간선들은 변수들 즉, 육상 경기 종류(100m, 200m ...)를 나타낸다고 했다. 그럼 방향이 같은 빨간선들(정확하게 말하면 같은 방향의 벡터인 변수들)끼리는 어떤 상관관계를 갖고 있을까? 다음 그림을 보자.
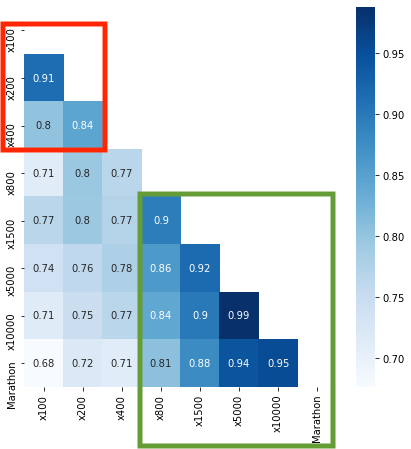
빨간색 네모칸을 보게되면 100m, 200m, 400m 간에 매우 강한 상관관계가 나타나는 것을 볼 수 있다. 또한 초록색 네모칸을 보게 되면 800m이상 주로 장거리 육상 종목끼리도 매우 강한 상관관계를 나타냄을 알 수 있다. 이로 보아 biplot에서의 변수들의 벡터들이 서로 같은 방향을 가리킨다면 서로 상관관계가 강한 변수들이라고 판단할 수 있다.
그렇다면 우리나라(South Korea)는 종합점수가 몇 위일까? PC1 값을 기준으로 내림차순으로 정렬한 후 우리나라의 종합 순위를 살펴보자.
# 1번째 주성분을 오름차순으로 정렬해서 어떤 나라가 1번째 주성분 벡터값이 가장 높은지 살펴보기(-는 벡터의 방향임! 방향 상관없이 크기가 크면 됨!)
pca_1 = pca_df[['pca1']]
pca_1 = pca_1.sort_values(by='pca1', ascending=False)
pca_1 = pca_1.reset_index()
pca_1.index = pca_1.index+1
pca_1.index.name = 'Ranking'
pca_1 = pca_1.rename(columns={'index':'Country'})
pca_1

우리나라는 종합점수가 전체 국가 중 22위라는 사실을 알 수 있다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] Out Of Fold(OOF) 방법으로 모델 평가하기 (4) | 2021.01.11 |
|---|---|
| [ML] Bayesian Optimization으로 파라미터 튜닝하기 (0) | 2021.01.02 |
| [ML] 당신은 데이터를 올바르게 분할하고 있는가? (0) | 2020.11.12 |
| [ML] 데이터를 복구하는 Auto Encoder? (0) | 2020.11.07 |
| [ML] Hyperparameter tuning & Optimization in DNN (0) | 2020.10.31 |



