앞으로 전개할 내용은 Coursera 강의의 내용을 기반으로 필자가 직접 정리하는 내용이며 해당 컨텐츠 이외의 다른 강의에 관심이 있다면 여기를 참고해 수강해보자.
이번 포스팅에서는 딥러닝(Deep Neural Network)의 성능을 개선시키거나 마주하는 문제들을 해결하기 위한 다양한 방법들에 대해 소개한다. 전개되는 내용들 중 일부는 이전 포스팅에서 게시했던 내용들과 중복될 수 있다. 그러한 내용들은 간단히 개념에 대해 소개하고 자세한 내용은 관련 포스팅 링크를 첨부하겠다.

딥러닝이 직면하는 문제들은 다양하다. 하지만 본질적으로 딥러닝이 도달해야 하는 이상점은 바로 만들어진 딥러닝 모델이 어떠한 낯선 데이터를 만나더라도 올바른 예측을 하는 것이다. 즉, 딥러닝의 모델을 일반화(Regularization)시키는 것이다. 이런 목적을 달성하기 위한 다양한 방법들을 소개한다. 목차는 다음과 같다.
1. Split the data
2. Bias / Variance
3. Regularization methods
4. Normalization of data
5. Vanishing / Exploding gradients
1. Split the data
머신러닝 또는 딥러닝 모델을 학습시키고 테스트하는 과정에서 데이터를 보통 3파트로 나누어서 사용한다. 바로 Train, Development, Test 용 데이터이다.(여기서 Development란, Validation(검증)용 데이터와 동일하다)

위 그림과 같이 3개의 부분으로 나누며 보통 Train : Development : Test 비율은 6 : 2 : 2가 널리 통용되는 비율이라고 한다. 하지만 최근 빅데이터 세상에 직면하면서 트렌드가 Development, Test 데이터 비율을 매우 작은 값으로 부여하는 것으로 변화했다. 왜냐하면 Development, Test 데이터셋은 단순히 모델을 평가하기에만 충분한 데이터 양이면 되기 때문에 20%정도까지 필요가 없기 때문이다. 예를 들어 100만개의 원본 데이터셋이 존재할 때, Development, Test 데이터 개수는 각 1만개 씩 정도만 있어도 충분하다는 것이다.
따라서, 100만개 미만의 작은 데이터셋이면 비율은 6:2:2로, 그 이상의 큰 데이터셋이라면 Development, Test 데이터셋의 비율은 각각 10%내로 설정하는 것이 바람직하다.
그리고 Development, Test 데이터들의 분포가 서로 유사해야 한다. 즉, 클래스 불균형 같은 문제가 없어야 한다.
2. Bias / Variance
Bias는 편향, Variance는 분산이라고도 부른다. Bias와 Variance는 모델을 평가하는 기준으로써 이 두 메트릭을 통해 모델의 성능이 과대적합(Overfitting) 되었는지 과소적합(Underfitting)이 되었는지 확인할 수 있다. Bias와 Variance 값에 따라 발생하는 문제는 다음과 같이 정리할 수 있다.(참고로 하단 설명의 '테스트 데이터'는 '검증(또는 개발)용 데이터' 로 바꾸어도 일맥상통 한다)
- 높은 Bias = Underfitting 발생 : 학습 데이터 뿐만 아니라 테스트 데이터에서도 모델의 예측 성능이 낮을 때를 의미한다. 보통 선형함수로만 이루어진 모델에서 자주 발생한다.
- 높은 Variance = Overfitting 발생 : 학습 데이터에서는 모델의 예측성능이 뛰어나지만 테스트 데이터에서는 모델의 예측 성능이 현저히 낮을 때를 의미한다.

한 가지 참고할 점은 모델의 성능을 평가하기 위해서는 Optimal(Base) Error라고 불리는 특정한 기준이 있어야 한다. Optimal Error란, 흔히 '사람이 데이터를 갖고 직접 예측했을 때의 예측력' 이라고 할 수 있다. 예를 들어, 고양이, 강아지 이미지 데이터를 사람이 직접 보고 어떤 사진은 고양이이고 어떤 사진은 강아지라는 것을 아마 정확하게 분류할 수 있을 것이다. 따라서 이 때 Optimal Error는 0값이 되게 된다. 결국 분류 예측 정확도가 100%라는 의미이다. 따라서 이 Opitmal Error를 기준으로 해서 모델의 성능을 평가해야 한다는 점도 알아두자.
Bias가 문제가 존재할 경우, 학습 데이터에서 학습할 때의 Error와 이후 개발 데이터로 평가할 때의 Error를 살펴봄으로써 Error 수치가 증가한다면 조치를 취해 개발 데이터에서 미리 Bias 문제를 대비할 수 있다. 이 조치를 취하는 방법에 대해서는 다음 목차에서 다루겠다.
또한 고차원의 입력 데이터 즉, Feature 개수가 기하급수적으로 많아진다면 해당 모델은 높은 Bias, 높은 Variance 두 가지 문제 모두 발생할 가능성이 높다.
이제 그렇다면 Bias, Variance 가 높을 때 각각 대처하는 방법에 대해서 알아보자.
먼저 높은 Bias 문제가 발생하면 곧 과소적합(Underfitting)이 발생하는 것이다. 과소적합을 해결하기 위해서는 모델에 다음과 같은 조치를 취할 수 있다.
- 모델 복잡도 향상 : Hidden layer, Unit(Neuron) 개수를 늘려 더 큰 신경망을 구축한다.
- 모델을 더욱 더 오랫동안 학습시킨다.
- 파라미터를 최적화 하는 다른 알고리즘을 사용해본다.
이제 높은 Variance일 때를 살펴보자. 높은 Variance는 과대적합(Overfitting)이 발생시킨다. 과대적합을 해결하기 위해서서는 다음과 같은 액션을 수행할 수 있다.
- 더 많은 데이터 수집: 가장 최고의 해결방법이다. 하지만 데이터를 더 수집하는 일은 가장 어려운 일이며 비용도 가장 많이 드는 일이다.
- 새로운 신경망 구조를 재 구축한다.
- Regularized Network로 만들어준다. 즉, 일반화(Regularization)를 수행해주는 것인데, 이에 대해서는 자세히 다음 목차에서 다루겠다. 참고로 일반화를 수행해주면 반대로 Bias 수치를 약간 증가시킬 수는 있지만 큰 신경망 구조를 갖고 있는 상태라면 그 증가한 Bias 수치는 큰 수치가 아니기 때문에 크게 신경 쓸 필요가 없다.
3. Regularization methods
3-1. Lambda(λ) parameter
Regularization을 한국어로 '일반화'로 해석하면 된다. 일반화를 수행하기 위해서는 Cost function에 일반화 항을 추가적으로 붙여주면 되는데, 주로 매개변수는 λ(람다)를 사용한다. 다음 수식을 보면서 '일반화 항'이 어디에 추가되고 있는지 살펴보자.

주로 일반화 항은 개발 데이터 셋을 이용한 교차검증에 주로 사용한다. 이 일반화시키는 것을 Weight Decay 라고도 부른다.(참고로 학습률과 관련된 Learning Decay라는 개념도 존재한다)
일반화항을 추가하는 방식은 크게 2가지로 나뉘는데 제곱을 이용하는 L2 Norm, 절댓값을 이용하는 L1 Norm이 존재한다. 간단히 두 개념의 차이점에 대해 언급하자면 L2 Norm은 파라미터 값을 0이 아닌 0에 근접한 값들로 만듦으로써 파라미터가 커지는 것을 억제한다. L2 Norm을 적용한 Weight들을 Frobenius matrix라고도 부른다.
반면에 L1 Norm은 파라미터 값은 아예 0값으로 만들 수 있다. 파라미터 값을 0으로 만들 수 있기 때문에 Feature Selection 효과와 모델의 크기를 압축하는 효과가 존재한다. 이 L2 Norm, L1 Norm에 대한 자세한 수식, 그리고 이 두개를 활용한 Ridge Regression, Lasso Regression에 대해 알고 싶다면 여기를 참고하자.
그렇다면 위와 같이 일반화 항을 추가해줌으로써 즉, L2 Norm 또는 L1 Norm을 이용하면서 파라미터를 0에 가깝거나 0값으로 만들면 어떠한 효과가 발생하는 걸까? 바로 딥러닝의 Hidden layer의 Unit(Neuron)의 영향을 줄여버린다. 이렇게 줄임으로써 기존보다 덜 복잡한 신경망 구조가 된다. 그러면 어떤 것을 이용해 일반화의 정도를 조절할까? 바로 상수값인 λ(람다) 파라미터를 이용해 조절이 가능하다.
그런데 이 λ(람다)값에 큰 값을 부여하면 파라미터값이 모두 0에 가깝거나 0값으로 되어버린다. 여러 활성함수 중 tanh 함수일 경우, λ(람다)에 큰 값을 설정하면 파라미터(Weight)값들이 작아지며 이로 인해 활성함수를 적용하기 전의 결과값들도 작아지고 결국 선형함수로만 이루어진 신경망 구조가 된다. 이렇게 되면 복잡한 Decision boundary를 정의하지 못하게 되어 문제를 해결할 수 없게 된다.
3-2. Dropout
자세하게는 Inverted Dropout이라고 하며 최근에 CNN 이론 포스팅에서 언급한 적이 있었다. 간단하게 말하면 최종결과값을 출력하기 전 의 Hidden layer에서 해당 layer 안에 존재하는 Unit들 중 일부를 무작위로 제거하는 방법이다.

드롭아웃은 보통 역전파를 수행하기 이전에 적용한다. 즉 드롭아웃을 수행한 후 역전파를 수행해 파라미터를 업데이트해 나간다. 드롭아웃을 수행할 때 특정 layer안에 있는 Unit을 얼마나 제거할지는 keep_prob이라는 인자를 추가해 설정해줄 수 있다.
예를 들어 최종 출력값을 내기 이전 마지막 Hidden layer에서 드롭아웃을 수행해주는데, keep_prob을 0.8로 설정했다. 마지막 Hidden layer안에 Unit들은 총 100개가 존재한다. 그렇다면 keep_prob=0.8이기 때문에 기존 유닛의 80%만큼만 사용한다는 것이다. 즉, 100개 중 80개의 유닛만 사용하고 20개의 유닛은 제거한다는 것이다. 따라서 이 keep_prob값이 낮을수록 그 만큼 제거하는 유닛개수가 많음을 의미한다.
드롭아웃은 우리가 위에서 봤던 L2 Norm과 같은 일반화 방법과 동일한 역할을 한다. 하지만 드롭아웃은 L2 Norm 일반화를 수행할 때 Weight 파라미터 별로 부과하는 L2 Norm값이 다르다. 따라서 입력값의 스케일에 따라 L2 Norm 적용하는 정도가 달라진다. 예를 들어 가장 큰 Weight Matrix가 100 by 100 shape을 갖고 있다. 반면에 다른 작은 Weight Matrix는 20 by 20 shape을 갖고 있다. 이 때 큰 Weight Matrix는 작은 Weight Matrix에 비해 keep_prob 값을 낮게 설정한다. 그렇기 때문에 큰 Weight Matrix는 작은 Weight Matrix에 비해 삭제하는 유닛의 개수가 많아진다.
결국 keep_prob값을 낮게 설정하는 것은 L2 Norm의 λ(람다)값에 큰 값을 부여하는 것과 동일하며 큰 값일 수록 파라미터를 제한하는 정도가 커지며 일반화 정도가 커지는 것을 의미한다.(여기서 일반화 정도가 무한정으로 커진다 해도 좋은 것이 절대 아니다. 일반화 정도가 무한정으로 커진다면 Bias가 높아질 것이기 때문)
참고로, 입력 데이터에도 드롭아웃을 수행할 수는 있지만 이러한 경우는 거의 없다고 보면 된다.
하지만 드롭아웃도 단점이 존재한다. 바로 교차검증 수행시 최적의 keep_prob을 찾아야 하기 때문에 더 많은 하이퍼파라미터가 생긴다. 또한 드롭아웃을 수행하게 되면 그동안은 Cost function을 정확히 정의할 수 없다. 왜냐하면 드롭아웃을 수행할 때마다 제거되는 유닛이 다르기 때문이다. 따라서 Cost값이 감소하는지 확인하기 위해서는 반드시 드롭아웃을 수행하지 않는 상태이어야 한다.
그리고 이것은 단점은 아니지만 드롭아웃은 학습, 개발(검증) 데이터에만 적용을 하고 테스트 데이터에서는 수행해선 안 된다. 왜냐하면 테스트 데이터는 앞으로 계속적으로 예측해야 하기 때문에 만약 이 때 드롭아웃을 수행한다면 하나의 데이터를 예측할 때마다 드롭아웃을 수행할 때 제거되는 유닛이 매번 달라지기 때문이다. 그래서 결국 예측 수치에 노이즈만 더해줄 뿐이다. 따라서 학습, 검증 데이터에서만 드롭아웃을 수행하고 테스트 데이터에서는 드롭아웃을 수행하는 추가적인 스케일링이 필요하지 않다.
드롭아웃은 주로 컴퓨터 비전에서 자주 사용된다. 왜냐하면 이미지 데이터는 항상 부족한 실정이다. 따라서 부족한 데이터는 거의 과대적합 문제를 야기시키기 때문이다. 그래서 과대적합을 해결하기 위해서 드롭아웃을 자주 사용한다. 물론 드롭아웃을 무조건적으로 사용하기 보다는 드롭아웃을 수행하기 전 반드시 그 모델에서 과대적합 문제가 발생하는지 살펴보는 과정이 선행되어야 한다.
3-3. Other regularization methods
그동안 봐왔던 일반화 방법 이외에 다른 방법들도 존재한다. 먼저 Early stopping이 있다.Early stopping은 학습 시 Cost값이 감소하다가 언제부턴가 다시 증가할 때 다시 증가하는 그 시점까지만 학습을 하고 멈추는 것을 의미한다. 이 방법 또한 일반화 역할을 하며 과대적합 문제를 해결해준다.
Early stopping은 Cost를 최소화시키는 지점에서 Gradient descent(기울기 강하)를 멈추게하는 것과 동시에 과대적합 문제도 막는 것을 동시에 수행하도록 되어 있다. 이 2가지 목적을 하나의 도구인 Early stopping으로 수행하려는 것이 단점이 될 수 있다. 즉, 학습 시 Cost를 가장 최소화 했을 때의 시점에서의 파라미터를 갖고 있는 모델이 테스트 데이터에서 과대적합 문제가 발생하지 않을 것이라는 보장이 없다는 것이다.
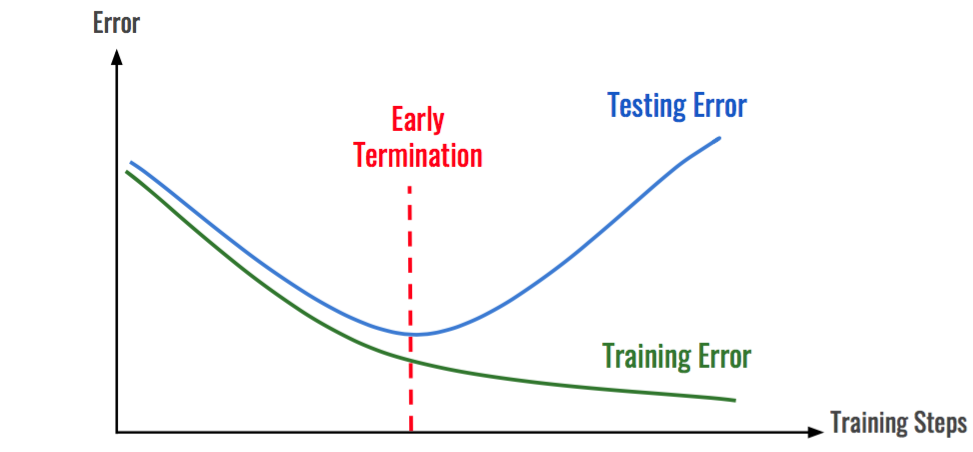
부가적으로 해당 Coursera강의의 강사이신 Andrew Ng 교수님께서는 보통 Early stopping 보다는 일반적인 L2 Norm을 사용해 λ(람다)값을 하이퍼파라미터로 설정해 일반화시키는 방법을 선호한다고 하신다. 왜냐하면 그 방법이 Computation 비용 문제에서도 좋기 때문이라고 한다.
다른 일반화 방법으로는 Data Augmentation이 있다. 이는 수치형 데이터보다는 주로 이미지 데이터에 적용할 수 있는 방법인데, 동일한 이미지 데이터를 좌/우 또는 상/하 반전 시키거나 확대/축소 또는 이미지를 일부러 찌그리트는 형태로 만들어 데이터를 증식시키는 것이다. 하지만 이 방법이 새로운 이미지 데이터를 수집하는 것보다는 효과가 절대 뛰어나진 않다. 다시 말해 새로운 데이터를 수집하는 것이 최고라는 것이다.

4. Normalization of data
입력 데이터 값을 표준화(Normalization)하는 것을 의미한다. 이를 수행하는 목적은 학습 속도를 높이기 위함이다. 그렇다면 데이터 값을 어떻게 표준화시킬까? 주로 각 입력값에서 평균값을 빼거나 0으로 만들고 표준편차로 나누어 준다.
만약 데이터를 표준화 시켜준다면 데이터의 분포가 어떻게 변할까? 다음 그림을 보자.

위 그림을 보면 표준화시킨 데이터는 이전보다 더 밀집해 있는 형태를 볼 수 있다. 표준화는 Gradient Descent를 수행하면서 최적의 파라미터를 찾는 즉, Global minimum을 찾아가는 과정과 밀접하게 연관되어 있다. 다음 그림을 보자.
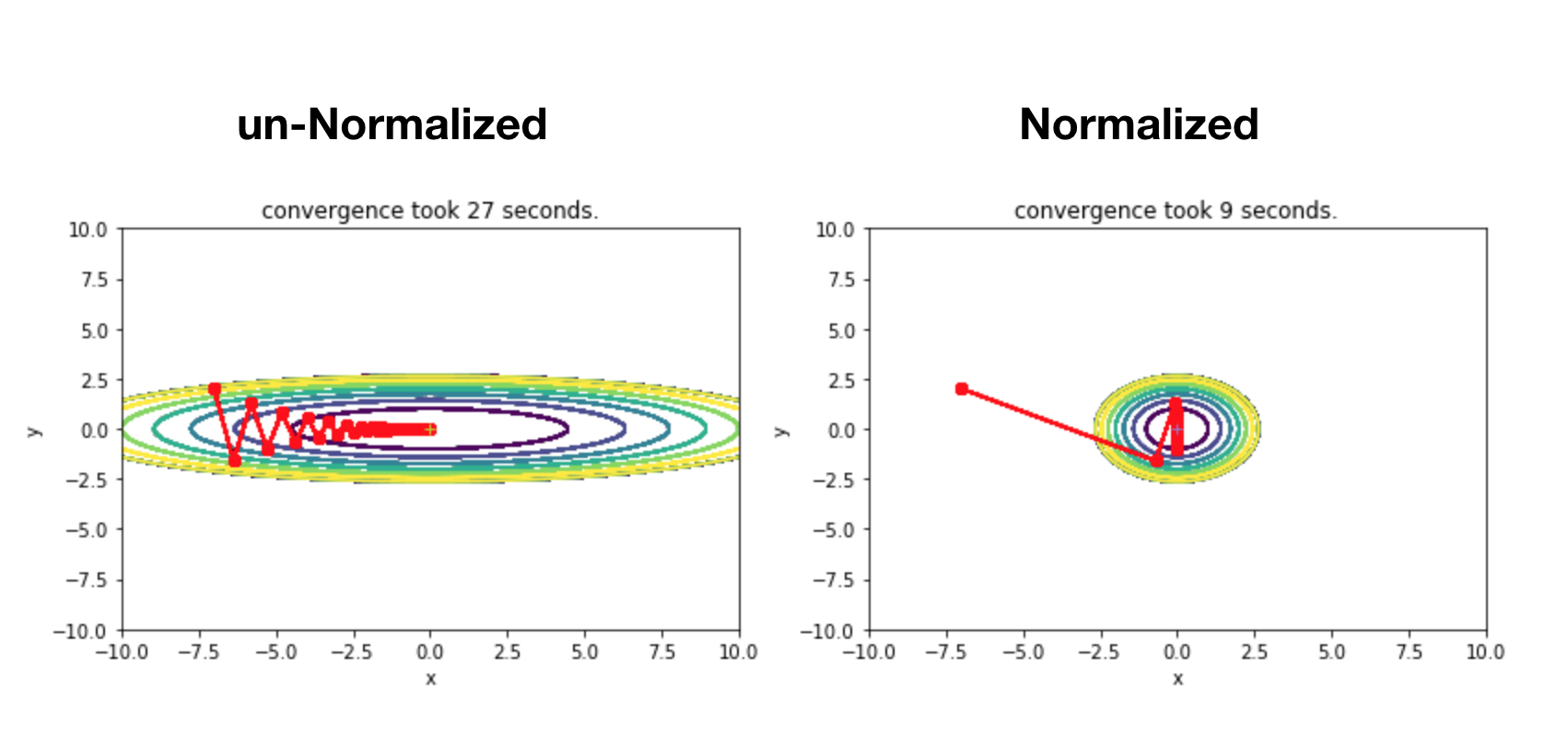
위 그림의 왼쪽을 보면 표준화 이전의 Cost function 형태를 보면 비대칭적인 나선형 모양을 띄는 것을 볼 수 있다. 이렇게 되면 빨간 색 직선들을 보는 것처럼 Global minimum(최적의 파라미터)을 찾아가는 데 이리저리 헤매(?)는 것을 볼 수 있으며 Converge 하는 데 27초가 걸렸음을 볼 수 있다.
반면에 오른쪽의 표준화 시킨 데이터의 Cost function 형태를 보면 대칭적인 모양을 띄는 것을 볼 수 있다. 이렇게 되면 학습 시작을 어느 지점에서 하더라도 Global minimum을 쉽게 찾아갈 수 있다. 그리고 Converge하는 데 약 9초 밖에 걸리지 않았다.
#Converge란, Global minimum을 찾았음을 의미한다.
5. Vanishing / Exploding gradients
Vanish는 사전적 의미로 '사라지다' 이며 Explode는 '폭발하다'라는 의미이다. 즉, Gradient(기울기)가 사라지거나 폭발(발산)하는 현상을 의미한다. 결론적으로 이러한 문제들이 발생하면 좋지 않은 상황이다. 왜냐하면 이와 같은 문제들이 발생한다면 Global minimum을 제대로 찾아갈 수 없기 때문이다.
이러한 문제를 부분적으로 해결하는 방법은 모델의 파라미터 초기값을 적절하게 설정해주는 것이다.
5-1. How to initialize parameters
파라미터를 초기화하는 적절한 방법은 우선 활성함수 종류에 따라 나뉠 수 있다. 먼저 Relu 함수일 때는 He 초기화 방법을 사용하며 Python의 Numpy를 이용해 공식을 정의하게 되면 np.random.randn(shape) * np.sqrt(2/n[layer-1]) 이 된다.(n[layer-1]은 layer-1번째 층에서의 Unit 개수를 의미)
반면에 tanh 함수일 때는 Xaiver 초기화 방법을 사용하며 이 또한 Numpy를 이용해 공식을 정의하면 np.random.randn(shape) * np.sqrt(1/n[layer-1]) 이다. 추가적으로 파라미터를 0으로 초기화하거나 정규분포로 초기화할 수 있는데 이렇게 하면 안되는 이유에 대해서는 여기를 참고하자.
5-2. Checking gradients
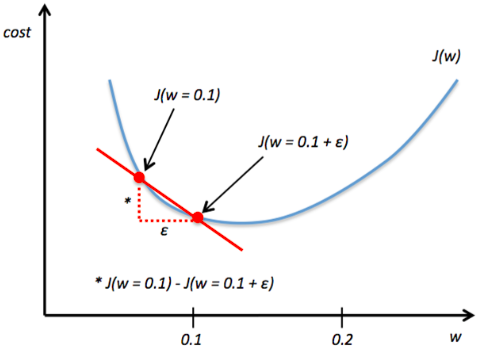
그렇다면 기울기(Gradients)가 사라지거나 발산할 때를 어떻게 발견할까? 우선 W,b값과 같은 파라미터값들을 하나의 벡터로 만들어 준다. 그리고 two-sided difference 공식을 이용한다. 입실론과 같은 임의의 값을 추가한 쎄타의 기울기(미분)값과 입실론을 추가하기 이전 쎄타의 기울기값의 차이를 유클리디안 거리 공식을 이용해 계산해 두 벡터의 차이를 구한다. 그리고 두 벡터를 더한 값으로 나누어 표준화를 시켜준다.
이렇게 구한 공식에서 입실론으로 특정 값을 대입해준 후 위의 공식을 계산 후 결과값이 방금 설정한 특정한 입실론값 보다 작으면 적절한 Gradient라고 판단하며 만약 크다면 부적절한 Gradient라고 판단한 후 데이터 요소들을 일일이 확인하면서 이상이 있는 값을 체크한다.
(이에 대한 자세한 내용은 Coursera 강의를 참고하길 바랍니다)
기울기를 체크할 때 몇 가지 주의해야 할 사항이 있다. 우선 모델이 학습할 때에는 기울기를 체크해서는 안된다. 오로지 이상한 기울기가 발견되고 디버깅할 때만 사용한다. 왜냐하면 학습시에도 기울기 체크를 같이 수행할 시 학습속도가 너무 느려지게 된다.
또한 과대적합을 예방하기 위해 Cost function에 일반화 항을 추가했다면 기울기 체크시 추가한 일반화 항을 염두에 두자.
그리고 기울기 체크는 드롭아웃에서는 동작하지 않는다. 왜냐하면 기울기를 체크할 때는 정확한 Cost function이 정의되어야 하는데, 드롭아웃을 수행하면 위에서 언급했다시피 정확한 Cost function이 정의되지 않기 때문이다. 따라서 기울기 체크는 반드시 드롭아웃이 적용되지 않은 상태에서 수행되어야 한다.
마지막으로 파라미터(Weight, Bias)값을 랜덤값으로 초기화시켰는데 0에 근접한 값들일 경우, 이 상태에서 Gradient Descent 하강을 수행하면 Vanishing gradients 문제가 발생할 수도 있기 때문에 처음에는 신경망 모델을 어느정도 학습시켜 파라미터값들을 0값으로부터 멀어지게 만든 후 기울기 체크를 실행하는 것이 바람직하다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] 데이터를 복구하는 Auto Encoder? (0) | 2020.11.07 |
|---|---|
| [ML] Hyperparameter tuning & Optimization in DNN (0) | 2020.10.31 |
| [ML] Recurrent Neural Network(RNN) (0) | 2020.10.16 |
| [ML] Class imbalance 해결을 위한 다양한 Sampling 기법 (0) | 2020.09.20 |
| [ML] How to correlate one or two categorical variables? (0) | 2020.09.15 |



