🔉해당 포스팅에서 사용된 자료는 고려대학교 산업경영공학부 김성범교수님의 Youtube 강의자료에서 발췌했음을 알려드립니다. 혹여나 출처를 밝혔음에도 불구하고 저작권의 문제가 된다면 joyh951021@gmail.com으로 연락주시면 해당 자료를 삭제하겠습니다. 감사합니다.
이번 포스팅에서는 그동안 확률분포 관련 포스팅에서 다루어보지 않았었던 감마, 베타, 카이제곱 분포, 그리고 t분포와 F분포에 대해 알아보려고 한다. 각 확률분포에 대한 PDF 함수 공식과 분포 생김새도 알아보며 서로가 어떤 관련이 있는지에 대해서도 알아보자. 목차는 다음과 같다.
1. 감마 분포
2. 베타 분포
3. 카이제곱 분포
4. t분포
5. F분포
1. 감마 분포
감마분포와 다음 목차에서 소개할 베타분포는 기본적으로 지수분포와 관련되어 있다. 감마분포는 지수분포의 일반화된 형태라고 볼 수 있으며 k개의 사건들이 발생할 때까지 걸리는 시간을 확률변수로 한다. 우선 감마분포의 PDF 함수를 살펴보자.

위 함수에서 λ는 지수분포에서의 단위 시간당 발생하는 사건 평균 건수를 의미한다. 그리고 α는 지수분포의 개수를 의미한다. 여기서 지수분포의 개수란 무엇을 의미하는 걸까?
예를 들어, 파라미터 λ값을 갖는 하나의 지수분포를 독립적인 확률변수로 하는 X1 부터 Xα 까지의 α개수만큼의 확률변수가 있을 때, 이 X1 ~ Xα까지를 모두 더한 값을 확률변수로 하는 새로운 확률변수 Z는 바로 α와 λ를 파라미터로 갖는 감마분포를 따른다는 것이다.
이 때, α = 1 일 때는 지수분포가 된다. 이유는 위에 설명했던 바와 동일하다. α = 1 이라는 것은 파라미터 λ값을 갖는 지수분포가 하나밖에 없다는 것이고 이는 결국 지수분포라는 것을 당연하게 알 수 있다.

다음은 감마 분포의 기댓값과 분산의 공식이다.

그렇다면 이 두 개의 파라미터 α, λ값에 따라 감마 분포의 모양이 어떻게 바뀌는지 살펴보자.

그림의 왼쪽은 λ값을 고정시켰을 때, α값에 따른 모양의 변화이며 오른쪽은 α값을 고정시켰을 때, λ값에 따른 모양의 변화이다.
2. 베타 분포
베타 분포는 감마 분포와는 달리 '비율'을 설명하는 분포라고 할 수 있다. 실제 응용사례를 예로 들자면, 제품의 불량률, 기기의 작동률 등과 같은 예시를 들 수 있겠다. 그리고 베타 분포는 감마 분포로 구성되어 있다. 즉, 공식에 감마 함수가 들어가 있다는 것이다.
베타 분포는 어떤 사건이 발생하는 비율을 확률변수로 하며 베타 분포의 PDF 함수식은 다음과 같다.

위 그림과 같이 베타 분포의 PDF 식에는 감마 함수가 들어가 있는 것을 볼 수 있다. 다음 그림은 베타 분포의 특징으로 이러한 특징이 있다고 알아두기만 하자.

이제 베타 분포의 기댓값과 분산 공식을 알아보자. 다음과 같이 α, β로 이루어져 있다.

다음은 베타 분포의 파라미터인 α, β 값에 따라 베타 분포의 생김새 차이를 살펴보자.

이 때 α, β값이 서로 갖던 틀리던 α, β값 모두 1보다 작은 값일 때 분포 형태를 보자. 마치 U자 곡선을 그리는 형태가 된다. 이 U자 모형의 곡선 분포가 바로 수명분포 즉, 위에서 자주 응용된다던 고장률, 작동률과 같은 예시에 사용되는 분포 모양임을 알아두자.
3. 카이제곱 분포
카이제곱 분포는 표본 분산(Sample Variance)의 분포를 의미한다. 정확히는 자유도 n-1을 가지면서 카이제곱 분포를 따른다.(이 때, n은 관측치 즉, 표본의 개수이다.) 그렇다면 카이제곱 분포는 무엇일까?
카이제곱 분포는 표본 정규분포를 각각 제곱해서 합한 새로운 확률변수가 따르는 분포이다.

다음은 카이제곱 분포의 PDF 함수와 기댓값, 분산 공식을 살펴보자.

그리고 감마 분포의 공식에서 α값이 v/2 이고 λ값이 2일 때는 특별한 케이스로 카이제곱 분포를 따른 다는 것도 알아두자.(1번 목차의 감마분포 PDF 함수식에 α값에 v/2을, λ값에 2를 대입해보자)
다음은 카이제곱 분포의 생김새를 살펴보자. 다음과 같이 오른쪽으로 기울어진 right skewed 분포의 모습을 볼 수 있다. k값은 자유도값으로 k값에 따라 카이제곱분포의 모양이 어떻게 달라지는지 밑의 그림을 관찰해보자.
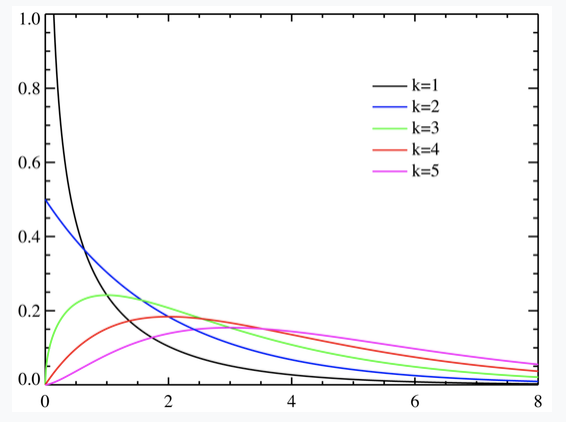
4. t분포
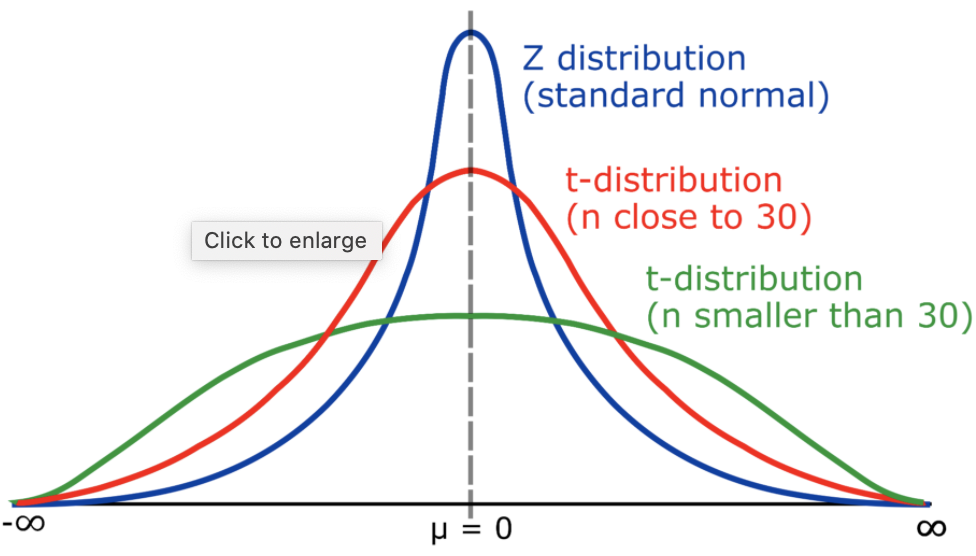
정확한 이름은 스튜던트 t분포로, t분포는 우리가 이전에 배웠던 것처럼 모분산 값을 모르는 상태에서 표본 개수가 30개 미만일 때 t분포를 이용한다고 배웠었다. 더 자세하게 t분포는 표준정규분포와 카이제곱분포의 결합으로 이루어져 있다. 물론 모양이 대칭이지만 정규분포는 아님을 알아두자.
5. F분포
F분포는 카이제곱분포 2개의 비율의 확률 분포를 의미한다. 그런데 표본분산은 카이제곱 분포를 따르므로 결국 F분포는 표본분산의 비율을 의미한다. 그렇기 때문에 두 집단의 등분산을 검정할 때 F-검정을 하는 이유도 이 때문이다.
F분포는 두 집단과 관련되어 있기 때문에 두 집단의 자유도와 관련이 있다. 이 자유도와 관련되서 주의해야 할 특성이 있는데 다음 그림을 보자.

위 그림과 같이 자유도 v1, v2를 갖는 각 두 집단의 F분포 확률을 구할 때 fα 와 fα-1 간의 관계는 역수를 취해주면서 동시에 자유도 순서 v1, v2를 v2, v1으로 바꾸어 주어야 한다.
'Data Science > 확률 및 통계' 카테고리의 다른 글
| [통계] 표본분산을 통한 모분산 예측과 카이제곱 분포 (2) | 2020.04.02 |
|---|---|
| [통계] 표본평균 (Sample Mean)을 통한 모평균 예측 (0) | 2020.04.01 |
| 퓨리에(Fourier) 변환과 확률변수의 특성함수 (0) | 2020.03.30 |
| 두 확률변수로 만드는 또다른 두개의 확률변수 (0) | 2020.03.29 |
| 이산확률변수의 합과 컨볼루션(Convolution) (0) | 2020.03.28 |



