이번 포스팅에서는 Linear Discriminant Analysis(LDA)인 선형판별분석과 Singular Value Decomposition(SVD)인 특이값 분할을 어떻게 구현할 수 있는지에 대해 살펴보려고 한다. 본 포스팅에서는 개념에 대해서는 간단히 다루므로 보다 깊숙한 개념은 여기를 참고하자.
목차는 다음과 같다.
1. LDA 구현해보기
2. SVD 구현해보기
1. LDA 구현해보기
LDA는 PCA와 비슷하게 입력 데이터셋을 저차원 공간으로 축소하는 기법이다. 하지만 PCA와는 다르게 LDA는 지도학습의 분류문제를 해결하기 수월하도록 클래스를 가장 잘 분류할 수 있는 선형을 최대한 잘 유지하는 축을 찾아준다는 차이점이 있다. LDA에 대한 목적함수나 수식에 대해서는 해당링크를 참고하자.
LDA는 Scikit-learn에서 API로 제공을 하고 있다. 간단한 데이터에 적용해보자.
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
iris = load_iris()
#Scaling features
scaler = StandardScaler()
iris_scaled = scaler.fit_transform(iris.data)
# PCA와 유사하게 축소할 Components 수를 지정하자.
lda = LinearDiscriminantAnalysis(n_components=2)
# LDA는 특이하게 fit 함수를 호출 시 종속변수(y값)을 넣어준다.
# 왜냐하면 클래스를 최대한 잘 분류할 수 있는 축을 찾아내기 위함이다.
# 그래서 종속변수값을 알고 있는 상태에서 모델링이 진행되기 때문에 지도학습 분류문제에 사용된다.
lda.fit(iris_scaled, iris.target)
# Scaling된 feature를 LDA활용해 차원축소시키기
iris_lda = lda.transform(iris_scaled)
print(iris_lda.shape)
LDA를 적용하여 차원 축소한 후의 feature를 기반으로 클래스값에 따른 데이터들의 산포도를 시각화해서 관찰해보자.
# 차원 축소시킨 후 데이터들의 산포도 살펴보기
import pandas as pd
import matplotlib.pyplot as plt
lda_columns = ['lda_com1', 'lda_com2']
iris_df = pd.DataFrame(data=iris_lda, columns=lda_columns)
iris_df['target'] = iris.target
markers = ['^', 's', 'o']
for i, marker in enumerate(markers):
x_axis_data = iris_df[iris_df['target']==i]['lda_com1']
y_axis_data = iris_df[iris_df['target']==i]['lda_com2']
plt.scatter(x=x_axis_data, y=y_axis_data, marker=marker,
label=iris.target_names[i])
plt.legend()
plt.xlabel('lda_com1')
plt.ylabel('lda_com2')
plt.show()

2. SVD 구현하기
SVD는 직각행렬에 적용할 수 있는 분해방법이다. SVD의 종류에는 여러가지가 있는데 자세한 종류는 여기를 참고하자. SVD는 Numpy, Scipy, Scikit-learn 라이브러리에서 각기의 방식으로 SVD의 API를 제공한다.
먼저, 아무것도 축소하는 것 없이 단순히 분할만 하며 원본 행렬로 복구가 가능한 Full SVD를 구현하는 코드를 살펴보자.
# numpy의 svd 모듈
import numpy as np
from numpy.linalg import svd
# 4 by 4 행렬생성
np.random.seed(42)
a = np.random.randn(4,4)
print(np.round(a, 3))
# 반환된 분해된 행렬 확인해보기
# 디폴트 SVD는 Full SVD임
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('U matrix \n', np.round(U,3))
# Sigma 행렬은 1차원으로 도출되는데 이는 0이아닌 대각행렬의 요소값을 제외한 0값들은 출력을 안하기 때문.
print('Sigma matrix \n', np.round(Sigma, 3))
print('Vt matrix \n', np.round(Vt, 3))
# 분해된 행렬 다시 원상복구해보기
# Sigma 행렬의 대각요소 제외한 0부분 다시 원상복구 시키기
Sigma_mat = np.diag(Sigma)
# np.dot은 행렬끼리 내적시키는 연산
a_ = np.dot(np.dot(U, Sigma_mat), Vt)
print(np.round(a_, 3))
다음은 차원을 축소하지만 0인 값들만 축소하므로 원본 행렬로 복구가 가능한 Compact SVD이다.
# Compact SVD 수행해보기
# 데이터 의존도가 서로 존재하는 행렬 임의로 생성
a[2] = a[0] + a[1]
a[3] = a[0]
print(np.round(a,3))
# SVD 분할 수행
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print(np.round(Sigma, 3))
# 분할 후 다시 복원
U_ = U[:, :2]
Sigma_ = np.diag(Sigma[:2])
Vt_ = Vt[:2]
print(U_.shape, Sigma_.shape, Vt_.shape)
a_ = np.dot(np.dot(U_, Sigma_), Vt_)
print(np.round(a_, 3))
다음은 0이 아닌 요소값들(주로 데이터에서 중요하지 않은 부분)을 제거하여 축소하기 때문에 원본 행렬로 복구하기는 힘든 Truncated SVD 구현코드를 살펴보자. 먼저 Scipy 라이브러리를 이용한 코드다.
# Truncated SVD 수행하기
# Truncated SVD는 Scipy의 spares의 svds 사용
# 일반 SVD는
import numpy as np
from scipy.sparse.linalg import svds
from scipy.linalg import svd
np.random.seed(12)
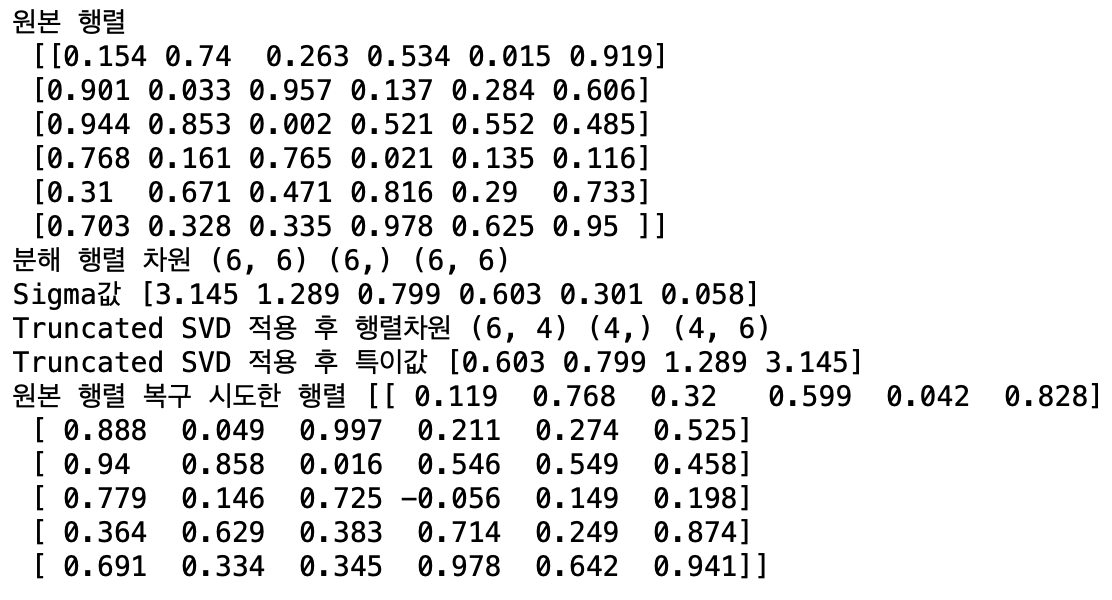
matrix = np.random.random((6,6))
print('원본 행렬\n', np.round(matrix,3))
# full_matrices=True면 U를 (M,M) Vt를 (N,N)으로 분할하고
# full_matrices=False면 U를 (M,k) Vt를 (k,N)으로 분할한다.
# 이 때, k= M,N 중 최소값임.
U, Sigma, Vt = svd(matrix, full_matrices=False)
print('분해 행렬 차원', U.shape, Sigma.shape, Vt.shape)
print('Sigma값', np.round(Sigma,3))
# Truncated SVD
# 특이값(대각행렬의 대각값들) 몇개로 할지 사전정의.
num_comp=4
U_tr, Sigma_tr, Vt_tr = svds(matrix, k=num_comp)
print('Truncated SVD 적용 후 행렬차원',U_tr.shape,Sigma_tr.shape,
Vt_tr.shape)
print('Truncated SVD 적용 후 특이값', np.round(Sigma_tr, 3))
# 다시 원본 행렬로 복구 시도해보기
matrix_tr = np.dot(np.dot(U_tr, np.diag(Sigma_tr)), Vt_tr)
print('원본 행렬 복구 시도한 행렬', np.round(matrix_tr, 3))
원본 행렬과 복구한 후 행렬 요소들을 비교해보면 값들이 비슷한 수치들이지만 Full, Compact SVD와는 달리 100% 일치하지 않는 것을 볼 수 있다.
다음은 Scikit-learn 라이브러리를 이용한 코드이다.
# Scikit-learn에서 제공하는 Truncated SVD이용
from sklearn.decomposition import TruncatedSVD, PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
iris = load_iris()
iris_features = iris.data
# 2개의 특이값으로 분할
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_features)
iris_tsvd = tsvd.transform(iris_features)
# 분할 후 데이터 산포도 시각화
plt.scatter(x=iris_tsvd[:,0], y=iris_tsvd[:,1], c=iris.target)
plt.xlabel('Comp1')
plt.ylabel('Comp2')

다음은 추가적인 내용인데, 바로 NMF(Non-negative Matrix Factorization)에 대한 내용이다. NMF는 Non-negative에서 유추해볼 수 있는 것처럼 원본 행렬 내의 모든 요소값들이 모두 0값 이상의 양수일 때 좀 더 간단하게 양수 행렬로 분할할 수 있는 기법이다. Scikit-learn에서 API를 제공하고 있으며 간단하게 적용 후 데이터를 시각화하면 다음과 같은 결과를 얻게 된다.
# NMF(Non-negative Matrix Factorization)
from sklearn.decomposition import NMF
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
iris = load_iris()
iris_features = iris.data
nmf = NMF(n_components=2)
iris_nmf = nmf.fit_transform(iris_features)
plt.scatter(x=iris_nmf[:,0], y=iris_nmf[:,1],
c=iris.target)
plt.xlabel('NMF comp1')
plt.ylabel('NMF comp2')

지금까지 LDA와 여러가지 종류의 SVD를 구현하는 방법에 대해 알아보았다. 끝으로 PCA, LDA, 다양한 SVD들은 모두 차원을 축소 즉, feature들을 축소시킴으로써 내재된(Latent) feature들을 새로 만드는 특징으로서 Feature Extraction이 기본임을 알아두자.
'Data Science > Machine Learning 구현' 카테고리의 다른 글
| [ML] Tensorflow를 이용해 Neural Network 구현하기 (0) | 2020.09.18 |
|---|---|
| [ML] K-means 와 GMM(Gaussian Mixture Model) 구현하기 (0) | 2020.08.13 |
| [ML] Scikit-learn을 이용한 PCA 구현하기 (2) | 2020.08.09 |
| [ML] Regression metric과 Polynominal Regression 구현하기 (2) | 2020.08.05 |
| [ML] Scikit-learn을 이용한 Feature engineering 구현하기 (0) | 2020.08.03 |



