이번 포스팅에서는 Categorical variables 즉, 범주형 변수들을 인코딩하는 여러가지 방법에 대해서 알아보려고 한다. 해당 내용은 포스팅 하단의 래퍼런스를 통해 학습했고 해당 래퍼런스에서 다루지 않는 다른 인코딩 방식이 존재한다면 댓글로 달아주시면 너무 감사할 것 같다.
범주형 자료에는 순서가 없는 명목형(nominal) 자료와 순서가 있는 순서형(ordinal) 자료로 나뉜다. 명목형 자료의 대표적인 사례로는 혈액형, 지역, 직업, 학교 등을 들 수 있다. 반면에 순서형 자료의 예시로는 생활수준, 만족도를 대표적으로 들 수 있겠다.
이러한 범주형 값들이 들어있는 데이터를 머신러닝, 딥러닝 모델의 input 데이터로 집어넣으려고 할 때 문자열 상태 그대로 모델에 넣을 수가 없다. 이러한 값들을 수치적인 값으로 인코딩을 해주어야 하는데 이 인코딩 하는 방법에는 여러가지가 있어 이에 대해 공부해보는 시간을 가졌다.
필자가 공부하기 이전에는 대표적인 one-hot encoding이나 label-encoding 같은 방법들만을 알고 있었다. 하지만 이번 기회를 통해 기존 방법 이외의 다른 여러가지 인코딩 방법들이 존재하고 인코딩 방법들도 상황에 따라 다르게 적용할 수 있다는 것을 알게 되었다.
이제 본격적으로 범주형 변수를 인코딩하는 방법들에 대해 알아보자.

1. One-hot encoding
원-핫 인코딩은 각 범주형 변수의 값들을 1과 0으로 매핑시키는 것이다. 아래 그림을 보면 직관적으로 원-핫 인코딩이 어떻게 이루어지는 알 수 있을 것이다.
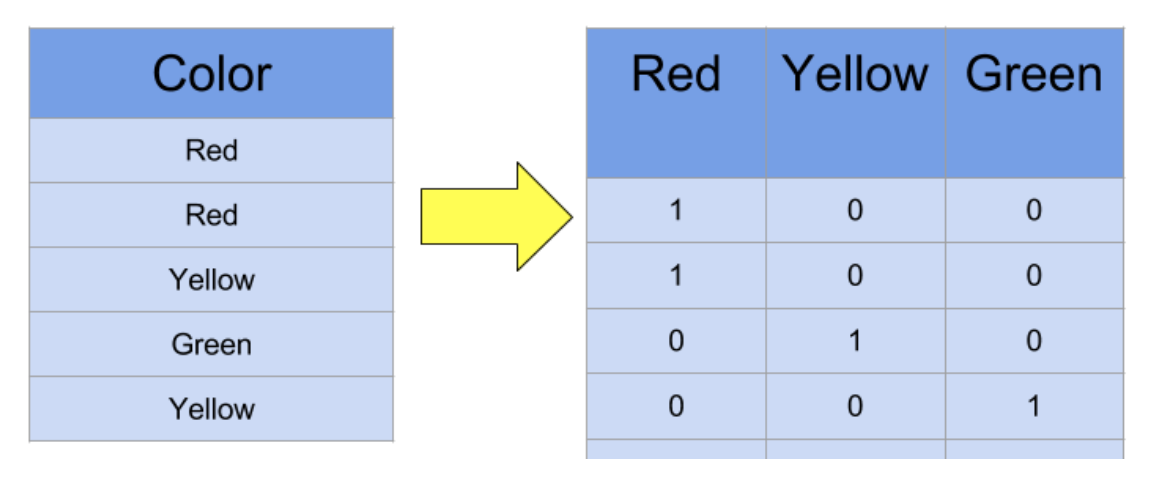
위 그림처럼 Categorical value인 Color의 값 종류가 3개 일 때, 원-핫 인코딩으로 변환하게 되면 특정 color값에 해당하는 값을 1로 하고 나머지는 0값으로 매핑시켜서 color 값 종류의 개수만큼 추가적인 변수(column)들을 만들어 낸다. 하지만 원-핫 인코딩은 범주형 변수 값들의 종류가 많아진다면 그 만큼 추가적으로 생기는 변수들이 많아지면서 모델링의 학습속도가 매우 느려진다. Python의 pandas에서는 get_dummies 함수로, scikit-learn에서는 one-hot encoding 함수를 개별적으로 각각 제공하고 있다.
원-핫 인코딩은 분류(Classification)와 회귀(Regression)문제 둘 다에도 자주 사용된다. 하지만 각 문제 종류에 따라 원핫-인코딩을 사용 시 차이점이 존재한다. 먼저 분류문제에서는 n개의 카테고리 값이 존재할 때 n개 카테고리 모두 인코딩을 해준다. 반면에 회귀문제에서는 n-1개의 카테고리값들을 인코딩해준다. 왜냐하면 자유도(degree of freedom)를 반영해주기 위함 때문이다. 선형 회귀(Linear regression)식은 학습되는 동안 모든 변수에 접근을 하게 된다. 이는 모든 정보를 선형회귀 모델에 전달한다는 것을 의미한다. 따라서 학습시간동안 모든 변수들(feature)을 동시에 접근을 하게되는 학습 알고리즘에 사용된다. 보통 SVM(Support vector machine)이나 ANN(Artificial neural network), 그리고 Clustering 알고리즘에 주로 사용이 된다.
2. Label-encoding
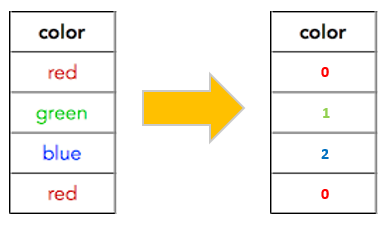
레이블 인코딩은 범주형 변수의 n개 종류의 값들을 0에서 n-1값으로 숫자를 부여한다. 이렇게 부여하게 된 숫자들 사이에서는 관계가 존재한다. 따라서 범주형 자료 중에서도 순서형 자료에 적합할 것이다. Python의 pandas에서는 factorize 함수를, scikit-learn 에서는 LabelEncoder 함수를 제공하면서 레이블 인코딩을 적용시킬 수 있다.
3. Ordinal-encoding
순서형 자료에 매우 적합한 인코딩 방식이다. 레이블 인코딩과 비슷할 수 있지만 레이블 인코딩은 인코딩을 하기 위해 들어오는 범주형 자료값들이 순서형 자료인지 아닌지 고려하지 않고 단순히 연속적인 숫자를 부여한다. 하지만 Ordinal 인코딩은 해당사항을 고려하게 된다.
그리고 데이터의 범주형 변수중 순서뿐만 아니라 알파벳 순서까지도 고려할 수 있다. Pandas를 사용하여 인코딩을 해줄 수 있긴 하지만 사용자가 주어진 범주형 변수를 보고 직접 변수 값들 간의 순서(order)를 dictionary 형태로 정의해주어야 한다. 그래서 직관적이긴 하지만 추가적인 코딩을 해야하는 수고가 필요하다.
4. Helmert-encoding
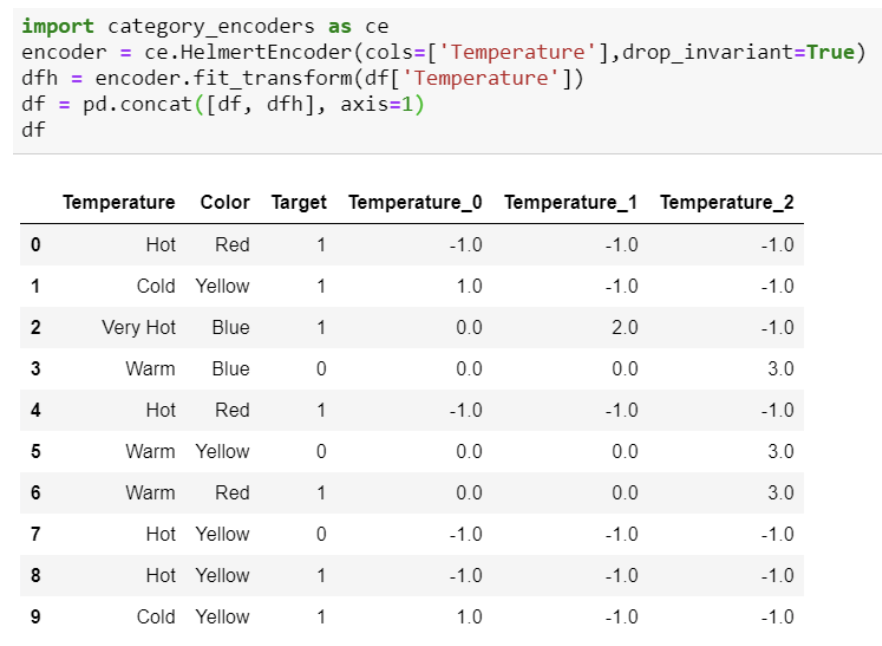
Helmert 인코딩은 특정 범주형 변수에서 특정한 level의 인코딩 값을 도출해내기 위해서 해당 level에 매핑되는 종속변수(dependent variable 즉, y값)의 평균값과 모든 level에 매핑되는 모든 종속변수값들의 평균값을 비교하는 방법이다. 잘 이해가 되지 않는다면 밑의 그림을 참고해보자. 인코딩하려는 범주형 변수는 Temperature이고 종속변수는 Target이다.
5. Binary-encoding
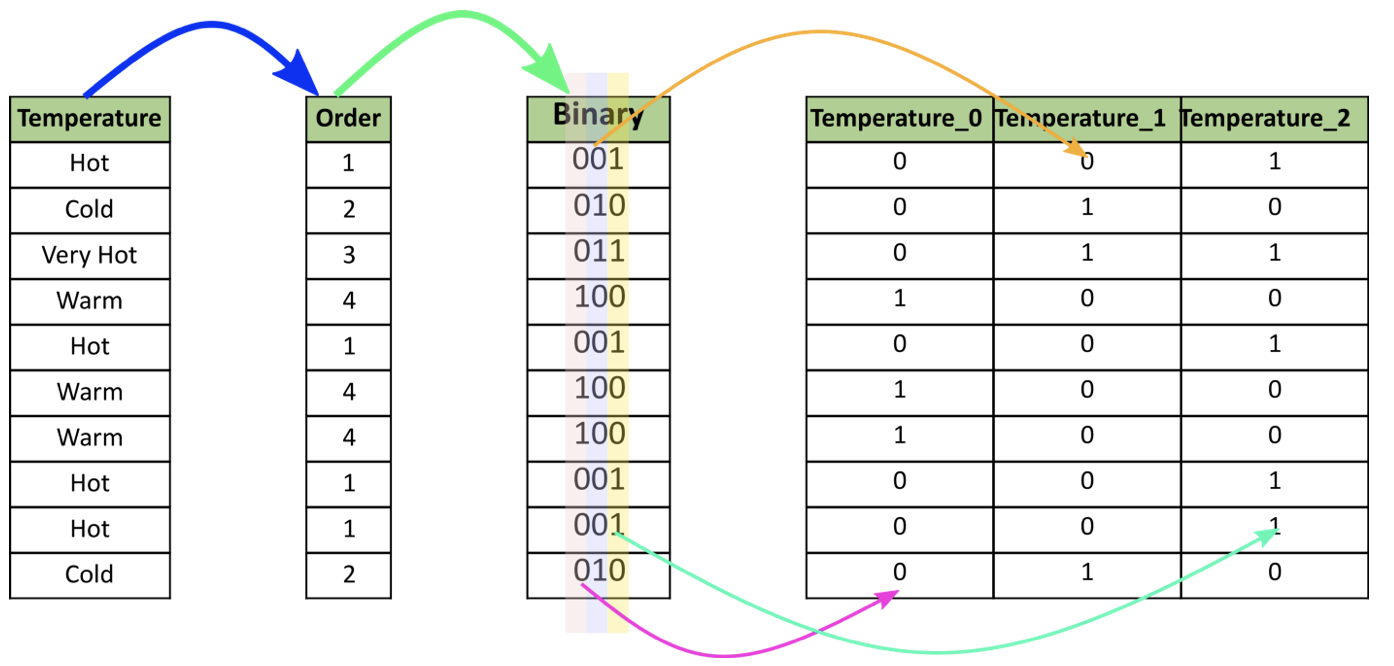
바이너리 인코딩은 범주형 변수값들을 이진법으로 변환해주는 방법이다. 만약 특정 범주형 변수에 n개 종류의 feature값들이 존재할 때, 바이너리 인코딩을 적용하게 되면 log2의 n제곱 feature개수만큼 변수들이 추가적으로 생성이 된다. 원-핫 인코딩과 비슷하게 feature 개수 만큼 추가적인 변수가 생성되지만 원-핫 인코딩에 비해 훨씬 더 적은 개수의 추가 변수가 생성된다. 따라서 모델링 학습시 속도가 원-핫 인코딩을 수행했을 때보다 빠르다. 바이너리 인코딩을 수행하면 아래 그림과 같이 변환되게 된다.
6. Frequency-encoding
범주형 변수 값들의 빈도수에 기반해 인코딩하는 방식이다. 이 방법은 해당 범주형 변수의 빈도값이 종속변수(y값)와 연관이 있게 된다면 모델이 가중치(weight값)를 부여하도록 도와주게 된다.
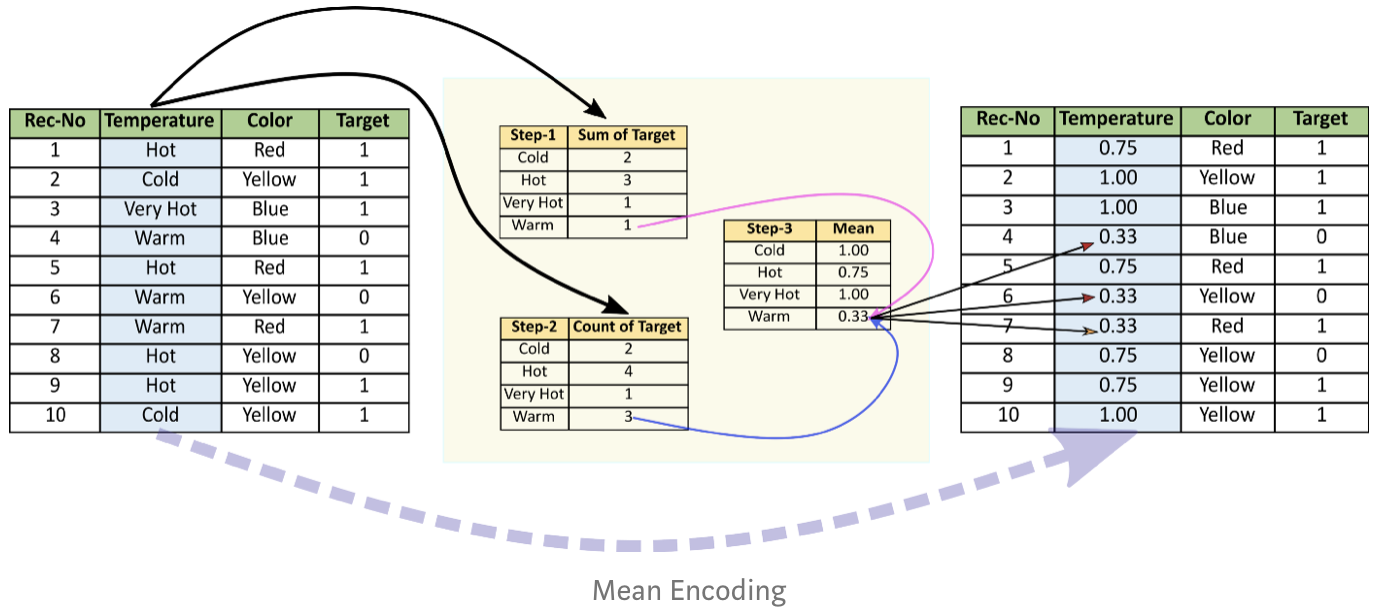
7. Mean-encoding
Target-encoding이라고도 부르며 기본적으로는 레이블 인코딩과 비슷하다. 하지만 범주형태의 독립변수들이 종속변수의 값들과 상관관계가 있음을 가정하는 것이 차이점이다. 그래서 범주형 독립변수 값들의 label들이 학습데이터에 존재하는 종속변수값들의 평균값으로 결정이 된다. 또한 레이블 인코딩은 그룹핑이 랜덤이지만 이 Mean-encoding은 많은 feature들이 있을 때 종속변수(y값)와 관련되어 그룹핑하게 된다.
비슷한 범주형값들 사이에서의 관련성을 도출하기는 하지만 그 관련성은 단지 학습 데이터라는 범위 안에서만 존재하는 것이다. 즉, 검증(test) 데이터에서도 관련성을 보장할 수 있도록 일반화할 수 없다는 의미이다.
데이터 양에 의해 영향을 미치지 않고 학습을 빠르게 해준다는 것이 장점이다. 하지만 과적합(Overfitting) 문제에 매우 취약해서 Cross validation이나 정규화(Regularization)와 같은 조치들이 필수적인 경우가 빈번하다.
이 인코딩 방법은 실력이 뛰어난 Kaggler들에 의해 개발된 방법으로 smoothing과 같은 다양한 응용방법들이 존재한다.
8. Weight of Evidence(WoE)
좋고 나쁨(이분법)을 구분하기 위한 그룹핑을 이용한 measure이다. WoE를 구하기 위한 수식은 다음과 같다.
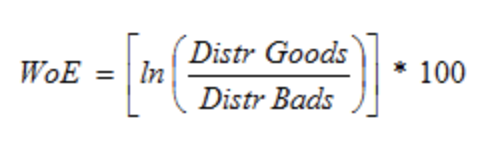
WoE값은 0이거나 0보다 크거나 작은 값이 되는데, 어떤 경우에 따라 WoE값이 달라지는지 살펴보자.
- if P(Goods) = P(Bads) , WoE = 0 이 된다. 이는 결과값이 도출되는 과정이 random하다는 의미이다.
- if P(bads) > P(Goods) , WoE < 0 이 된다.
- if P(Goods) > P(Bads) , WoE > 0 이 된다.
이분법에 적합하기 때문에 로지스틱 회귀에 매우 자주 사용된다. 하지만 정보손실량이 발생하는 단점이 있다. 또한 일변량(univariate)일 때 주로 사용된다. 왜냐하면 WoE 방법은 독립변수들이 여러개일 때 독립변수들간의 상관관계를 고려하지 않기 때문이다.
9. Probability Ratio of encoding
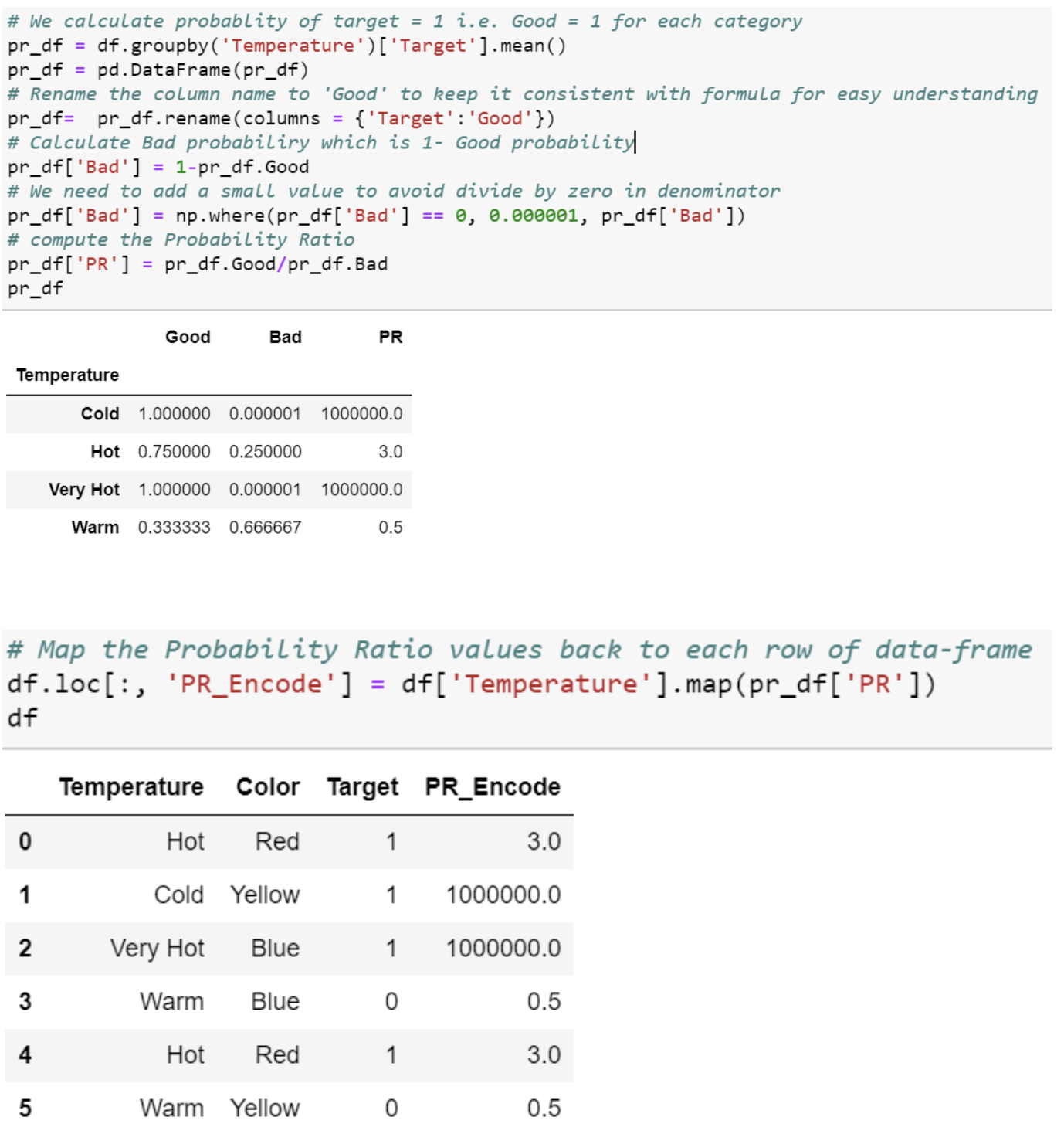
WoE와 유사한 방법이지만 좋고 나쁨 확률의 비율만을 사용한다는 것이 특징이다. 방금까지 언급했던 WoE의 수식을 보면 비율에 log를 취하는 등 추가적인 연산이 붙지만 이 방법은 단순히 비율만을 갖고 인코딩한다는 것이 특징이다.
WoE 방법도 마찬가지지만 이 방법을 사용할 때 나쁨(0값)이 될 확률의 최소값을 0이 아닌 값으로 설정해주어야 한다. 왜냐하면 나쁨 label이 아예 존재하지 않아서 비율을 계산할 때 0으로 나누어지는 상황을 방지하기 위해서다. 다음 그림은 해당 인코딩 방법을 사용한 예시이다.
10. Hashing
범주형 변수들을 더 높은 차원의 숫자공간으로 조작을 하는 방식이다. 범주형 변수들의 두 벡터사이의 거리가 높은 차원으로 변형된 공간에서도 유지될 때 사용한다.
원-핫 인코딩보다 차원 수가 훨씬 낮아서 데이터의 중복도(Cardinality)가 높을 때 사용하면 유용하다.
11. Backward difference encoding
특정 범주형 변수에서 하나의 level에 대한 종속변수값들(y값)의 평균이 바로 이전의 level에 대한 종속변수값들의 평균값과 비교되어 계산이 되는 방법이다. 주로 nominal, ordinal 변수에 적합하다고 알려져 있다.
12. Leave one out encoding
Mean encoding과 비슷하지만 이상치를 제외시킨 상태에서의 종속변수값들의 평균을 이용해 범주형 변수값들을 인코딩하는 방법이다.
이상치를 제거한다는 의미로 leave one out이라는 이름이 붙게된 듯 하다.
13. James-stein 인코딩
관측된 feature value와 관측되지 않은 feature value의 종속변수 값의 평균값들 중에서 다시 가중치를 부여한 평균값을 이용해 인코딩하는 방법이다. 이러한 방법은 전체적인 평균값(모평균)에 도달하기기 위해 위에서 구한 평균값들을 수축시킨다는 의미가 된다. 하지만 원본 데이터들의 분포가 졍규분포일 때만 적용이 유의미하다.
14. M-estimator encoding
Mean encoding을 단순화시킨 버전이다. 하나의 하이퍼파라미터값인 m값이 존재하는데 이 m값은 정규화의 강도를 의미한다. 따라서 m값을 높게 부여할수록 더 강력하게 정규화시키면서 제한강도가 높아진다. 권장되는 m값의 범위는 1~100사이의 값이다.
지금까지 범주형 변수의 값들을 모델이 알아들을 수 있도록 숫자값으로 인코딩하는 여러가지 방법들에 대해서 알아보았다. 포스팅을 작성하면서 공부했던 레퍼런스를 해석하면서 레퍼런스에 Q&A에 대한 좋은 답변이 있어서 추가적으로 남기려고 한다.
# Appendix
질문은 "y값들을 이용해 인코딩하는 방법을 사용할 때 만약 Test 데이터에서 y값이 존재하지 않을 때는 Test 데이터의 독립변수들을 어떻게 인코딩하는가?" 라는 것이었는데. 이에 대한 답변은 다음과 같다.
"Train 데이터에서 독립변수들을 인코딩하기 위해 사용했던 y값들을 Test 데이터에서도 똑같이 사용하면 된다. 이러한 방법은 Train 데이터에서 수치형 변수들을 Scaling할 때 사용했던 방법을 Test 데이터에서도 똑같이 사용하는 것과 똑같은 맥락이다."
#Refrerence
towardsdatascience.com/all-about-categorical-variable-encoding-305f3361fd02
All about Categorical Variable Encoding
Most of the Machine learning algorithms can not handle categorical variables unless they are converted to numerical values and many…
towardsdatascience.com
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] Multivariate regression(다변량 회귀분석) 프로세스 (0) | 2020.09.08 |
|---|---|
| [ML] Mean Shift, DBSCAN, and Silhouette metric (0) | 2020.08.14 |
| [ML] Spectral Clustering(스펙트럴 클러스터링) (4) | 2020.07.10 |
| [ML] GA(Genetic Algorithm) (7) | 2020.07.08 |
| [ML] Hidden Markov Model(HMM) (0) | 2020.07.04 |



