이번 포스팅에서는 시계열의 분해법에 대해 알아보려고 한다. 이번에 다룰 내용은 이동평균평활법을 활용한 분해법과 전통적인 분해법이다. 시계열 데이터를 각 개별성분(추세, 계절, 순환, 불규칙)으로 분해하고 다시 결합하여 미래의 값을 예측하기도 하지만 분해법의 주요목적은 '변동요인을 잘 구분하기 위함'이라는 것을 기억하자.
포스팅의 목차는 다음과 같다.
1. 이동평균평활법을 활용한 시계열 분해
2. 전통적인 시계열 분해법
1. 이동평균평활법을 활용한 시계열 분해
이동평균평활법은 시계열 데이터의 '불규칙 성분'을 제거하기 위해 사용되는 방법이다. 즉, 추세, 순환성분을 추정하기 위해 사용한다. 이동평균평활법은 또 대칭이동평균과 중심화이동평균으로 나뉘어진다.
-
대칭이동평균 : 이동평균시키는 값(m값)이 홀수인 경우에 사용한다.
-
중심화이동평균 : 이동평균시키는 값(m값)이 짝수인 경우에 사용한다.

2. 전통적인 시계열 분해법
전통적인 분해법은 우선 가법(additive), 승법(multiplicative)으로 두 가지 방법으로 나누어질 수 있다. 이 두 가지 중 하나를 선택하는 기준은 예전 포스팅에서 배웠던 '홀트-윈터스 계절모형'에서 가법/승법 중 모델을 선택하는 기준과 동일하다. 즉, 원본 데이터가 일정하게 안정적인 그래프를 그린다면 '가법', 증가하거나 감소하는 형태를 띈다면 '승법'으로 선택하면 된다.
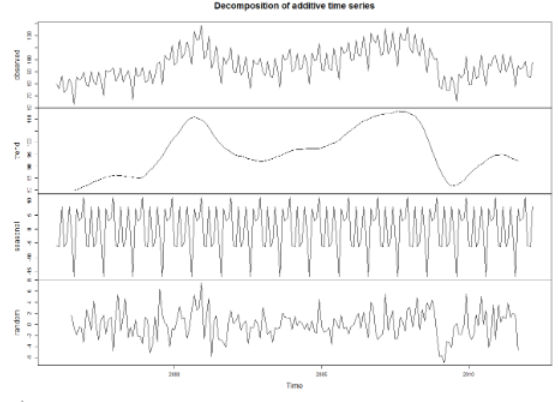
-
가법을 적용한 분해법
-
추세가 조정된 데이터를 보기 위해서는 [Raw data - Trend = Seasonal + 불규칙] 과 같이 해주면 된다.
-
보통 불규칙성분을 바로 추정하지 않기 때문에 불규칙 성분을 추정하기 위해서는 Raw data에서 Trend와 Seasonal 성분 하나씩 빼주면 된다.
-
-
승법을 적용한 분해법
-
추세가 조정된 데이터를 보기 위해서는 [Raw data / Trend = Seasonal * 불규칙] 과 같이 해주면 된다.
-
승법 또한 가법과 마찬가지로 불규칙 성분을 직접적으로 추정하지 않고 Raw data에서 Trend와 Seasonal성분을 하나씩 나누어 주면 된다.
-
하지만 전통적인 분해법은 추세, 순환 성분을 추정할 때 정보손실이 발생하며 이는 결국 불규칙 성분 추정시 정보손실이 발생하게 된다. 또한 급등하거나 급락하는 데이터 기간에 값이 크게 변화한다. 마지막으로 전통분해법은 계절성분 값이 주기별로 일정한 것을 가정한다. 따라서 단기간의 데이터를 분해하는 방식으로는 적합하지만 장기간의 데이터에는 부적합하다.

#포스팅에 쓰인 자료의 출처는 순천향대학교 빅데이터공학과 김영민교수님의 수업자료를 기반으로 했음을 알려드립니다.
'Data Science > 시계열(Time-Series) 분석' 카테고리의 다른 글
| AR(AutoRegressive), MA(Moving Average), ARMA Models (0) | 2020.07.14 |
|---|---|
| Box-Jenkins 방법론과 ARIMA 모델의 기초 (0) | 2020.07.14 |
| ETS 모델과 벤치마크로 미래의 값 예측하기 (0) | 2020.05.28 |
| 시계열 데이터(Time-Series) 분석, 예측방법 (0) | 2020.04.30 |
| 시계열 데이터(Time-Series Data)의 특징과 모형 (0) | 2020.04.27 |



