🔊 해당 포스팅은 밑바닥부터 시작하는 딥러닝 3권을 개인적으로 공부하면서 배운 내용을 기록하고 해당 책을 공부하시는 다른 분들에게 조금이나마 도움이 되고자 하는 목적 하에 작성된 포스팅입니다. 포스팅 내용의 모든 근거는 책의 내용에 기반하였음을 알립니다.

이번 포스팅에서는 그동안 만들어온 Dezero라는 딥러닝 프레임워크가 더 복잡한 모델인 CNN, RNN도 구현할 수 있도록 기능을 고도화해볼 것이다. 그리고 난 후 대표적인 CNN, RNN 계열 모델인 VGG16, LSTM 모델을 Dezero만을 활용해 빌딩해보도록 하자. 드디어 책의 마지막 챕터이다. 이제 그 끝을 향해 달려나가보도록 하자!
1. CNN 메커니즘 - 2차원일 경우
CNN을 코드로 구현하기 위해서는 CNN에 대한 개념 이해가 선행되어야 한다. 예전 포스팅에서 CNN에 대해 소개했었던 적이 있다. 컨볼루션, 패딩, 스트라이드에 대한 개념은 예전 포스팅을 참조하도록 하자. 여기에서는 CNN을 통해서 행렬의 형상이 어떻게 바뀌는지에 초점을 맞추어 메커니즘을 이해해보도록 하자. 이것에 포커스를 맞춰 이해하는 목적은 CNN을 우리가 Dezero로 구현해야 하기 위함이다.
대표적으로 알아야 할 개념은 다음과 같다. 컨볼루션(합성곱) 연산의 수행과정, 그 합성곱 연산에 기여하는 필터(또는 커널이라고도 하는데, 보통은 서로 다른 종류 커널의 모음을 필터라고 칭한다), 스트라이드, 패딩이다. 이것에 대한 개념은 예전 포스팅을 참조하도록 하고, 여기서부터는 입력층에 컨볼루션을 수행한 후의 출력층 형상(shape)를 계산하는 공식부터 배워보도록 하자.

수식에 대한 각 설명도 같이 적어놓았다. 참고로 큰 대괄호(big bracket)은 내림처리(floor 처리)를 의미한다. 위 수식을 잘 보면 알겠지만 패딩 크기를 늘리게 되면 출력층의 크기가 커진다. 이유는 패딩의 사이즈($P$)가 공식의 분자에 있기 때문이다. 반대로 스트라이드를 크게 한다면 출력층의 크기가 작아진다. 이유는 스트라이드의 사이즈($S$)가 공식의 분모에 있기 때문이다.
그리고 모든 미지수 값에 "(또는 너비)" 라고 적어놓은 이유는 입력층, 출력층, 커널, 스트라이드, 패딩 이 모두의 사이즈가 항상 높이와 너비가 같은 정사각형 형태가 아닌 직사각형 형태일 수도 있기 때문이다. 위 공식을 활용해서 출력층 형상을 추측하는 함수를 구현하면 아래와 같다.
def get_conv_outsize(input_size, kernel_size, pad_size, stride_size):
output_size = (input_size + 2 * pad_size - kernel_size) // stride_size + 1
return output_size
그래서 입력층이 2차원이고 채널 개수가 1개인 경우에(ex. 흑백사진 이미지) 컨볼루션을 수행하면 아래 그림처럼 도식화시킬 수 있다.

2. CNN 메커니즘 - 3차원/4차원일 경우
1번 목차에서 알아본 내용은 흑백 이미지 같이 채널 개수가 1개 밖에 없는 2차원 이미지, 또 이미지 데이터 개수가 1개일 경우에만 살펴본 것이다. 하지만 우리가 실제로 자주 마주하는 이미지 데이터의 형상은 컬러 이미지이기 때문에 채널 개수가 3개가 되어 3차원 이미지가 되고, 더 나아가 모델에 배치 사이즈가 1 즉, 단일 1개의 이미지만 넣지 않고 N개 이미지로 묶어 넣는 미니배치 형식으로 모델에 넣기 때문에 데이터 배치 개수까지 고려하게 되면 우리는 총 4차원 형상의 텐서를 다루게 된다.
3차원/4차원일 경우를 동시에 살펴보면 헷갈릴 수 있으니, 하나씩 정복해나가보자. 먼저 3차원일 경우 즉, 채널 개수가 3인 컬러 이미지를 다루며 데이터 개수가 1개일 경우 컨볼루션 수행하는 과정을 그림으로 나타내면 아래와 같다.

그런데 위 경우는 커널이 1개 즉, 적용할 커널의 종류가 1개 밖에 없을 경우이다. 보통은 이 커널의 종류도 개수를 늘려서 입력층의 다양한 특성을 포착할 수 있도록 해준다. 그래서 커널의 종류가 늘어난다면 아래 처럼 형상이 바뀐다.

이전과 차이점은 커널 개수가 OC개만큼 늘었다는 점이다. 그런데 여기서 주목할 점은 커널 개수를 늘려주게 되면 동시에 출력층의 채널 개수가 동일하게 같이 증가한다. 즉, 커널의 개수가 출력층의 채널 개수가 되는 셈이다. 따라서 위 그림의 파란색 화살표를 살펴보면 두 개가 OC라는 미지수로 똑같음을 알 수 있다. 반대로 입력층의 채널 개수는 커널의 채널 개수(커널의 개수가 아닌 커널의 '채널' 개수임에 주의)와 동일해야 한다.(빨간색 화살표)
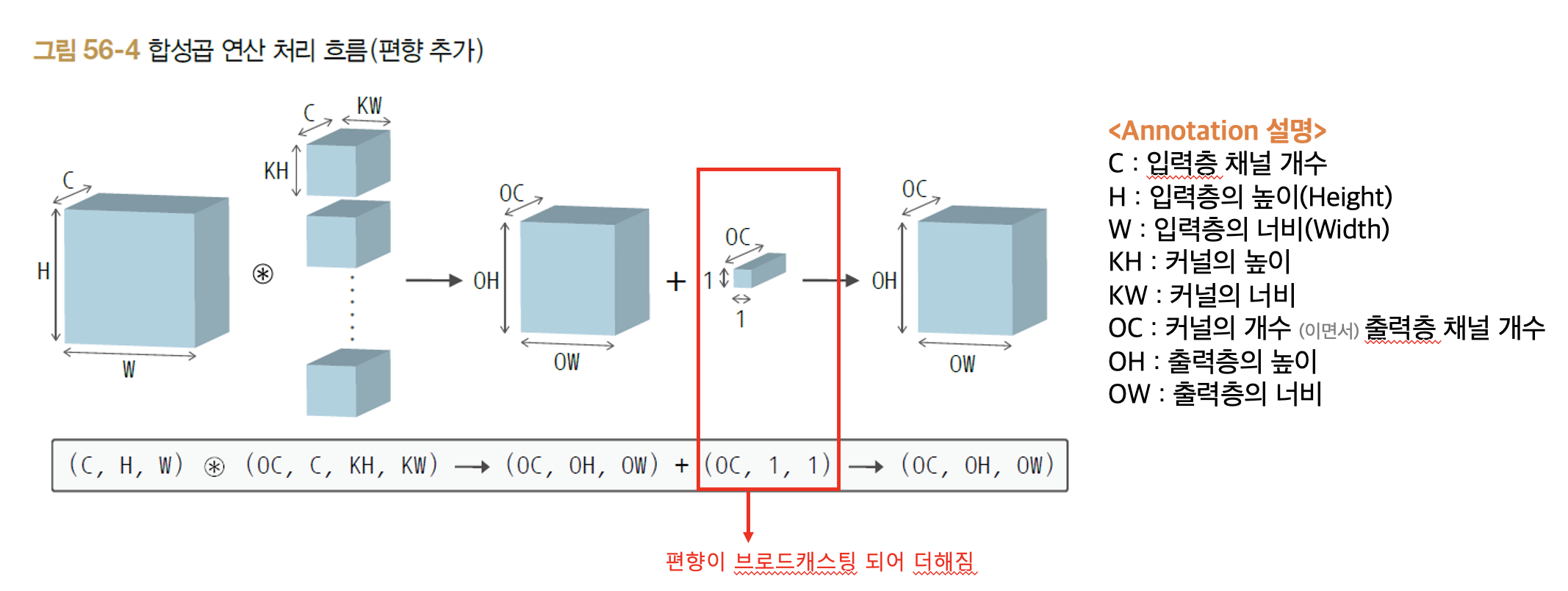
여기서 한 가지 추가적으로 알아두면 좋을 점이 있다. 컨볼루션도 어찌되었건 일반적인 DNN에서 사용하던 것처럼 선형 연산을 취해주면서 편향도 추가해줄 수 있다. 다음 그림은 편향 값이 추가되었을 때 형상이다. 컨볼루션에서의 편향은 채널 개수당 하나의 값을 갖는다. 그래서 컨볼루션 수행 후 나온 출력층의 형상만큼 브로드캐스팅되어서 단순히 더해주면 된다. 아래 그림처럼 말이다.
다음은 위의 경우에서 이미지 데이터가 N개로 늘어났을 경우 즉, 미니 배치일 경우에 컨볼루션 과정을 살펴보자.
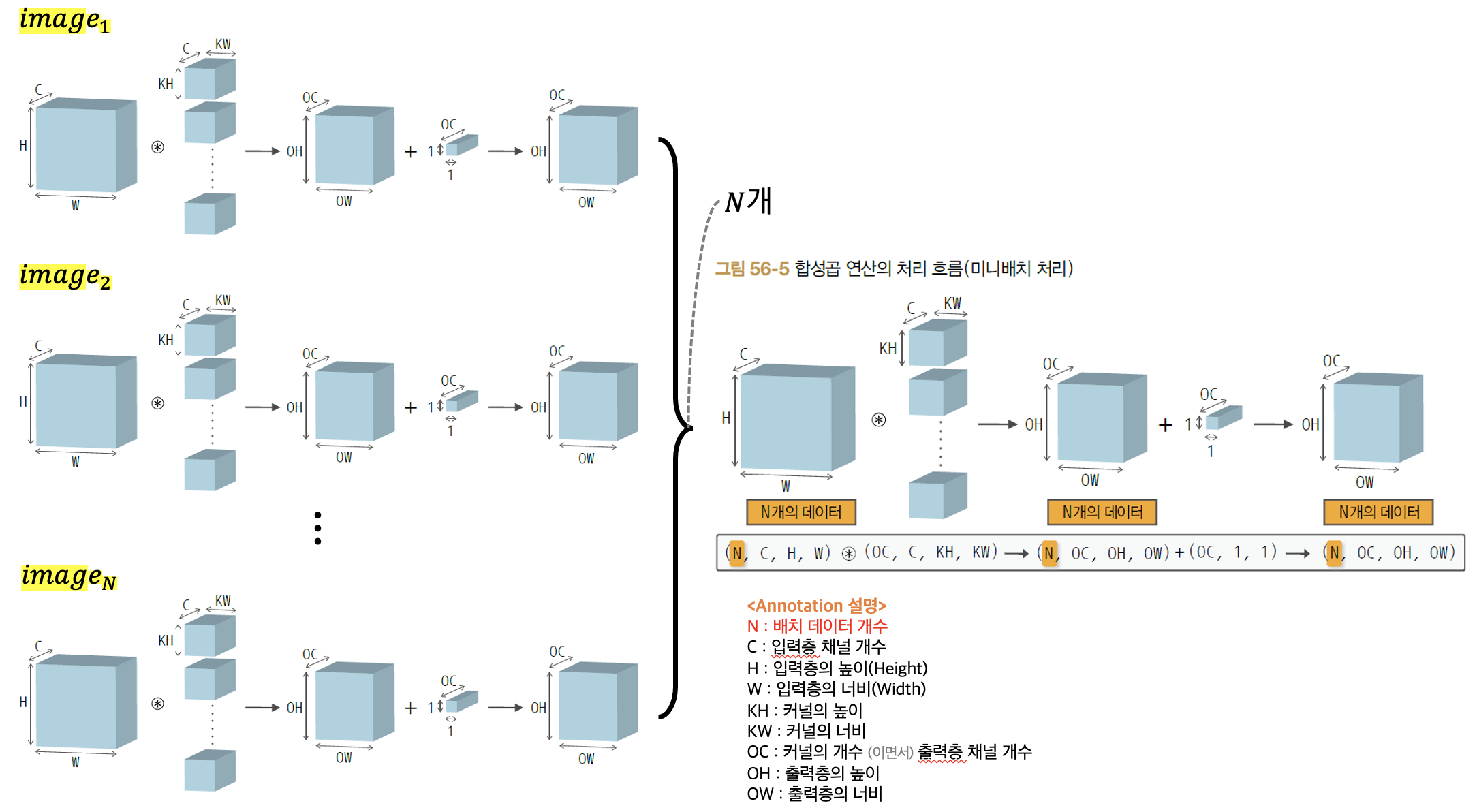
위 그림의 오른쪽 부분의 텐서 형상을 유심히 살펴보면서 자신이 이해하는 부분과 일치하는지 이해해보자. 한 가지 주의해야 할 점은 미니 배치 데이터 개수로 늘어남으로써 입력층, 출력층 개수는 차원이 1개 늘어나 4차원이 되었지만 커널의 모음인 필터의 차원는 여전히 이전과 마찬가지로 4차원 형태이다. 이 부분을 보고 "필터의 차원도 1차원이 더 늘어나서 (N, OC, C, KH, KW)의 형상이 되어야 하는게 아닌가?" 라고 생각할 수 있지만, N개의 이미지 각각에 적용되는 필터는 동일한 필터를 사용하기 때문에 4차원이 유지됨에 주의하도록 하자.
다음은 풀링층에 대해 알아두면 좋을 지식에 대해 간단히 짚고 넘어가도록 하자. 우선 풀링은 보통 Max 풀링을 사용하며 동작 과정은 간단하다. 단순히 풀링 사이즈에 해당되는 영역에서 '최댓값' 원소만 추출하면 된다. 이러한 풀링 윈도우 크기는 보통 풀링 스트라이드 크기와 같은 값으로 설정한다고 한다.
풀링층의 주요 특징은 크게 3가지가 존재한다. 우선 컨볼루션 층과는 달리 학습하는 매개변수가 존재하지 않는다. 이는 당연하다. 풀링층에 어떤 선형연산을 취해주는 것도 없고 단순히 최댓값 또는 평균값 등과 같이 대푯값에 해당하는 원소만 추출하면 되기 때문이다. 다음은 채널 수가 변하지 않는다는 점이다. 풀링 연산은 채널마다 독립적으로 이루어진다. 예를 들어, 채널 개수가 3이고 높이,너비가 4인 입력층에다가 풀링 윈도우 사이즈가 (2, 2), 풀링 스트라이드 사이즈도 (2,2)일 경우에 수행되는 그림은 애라와 같다.
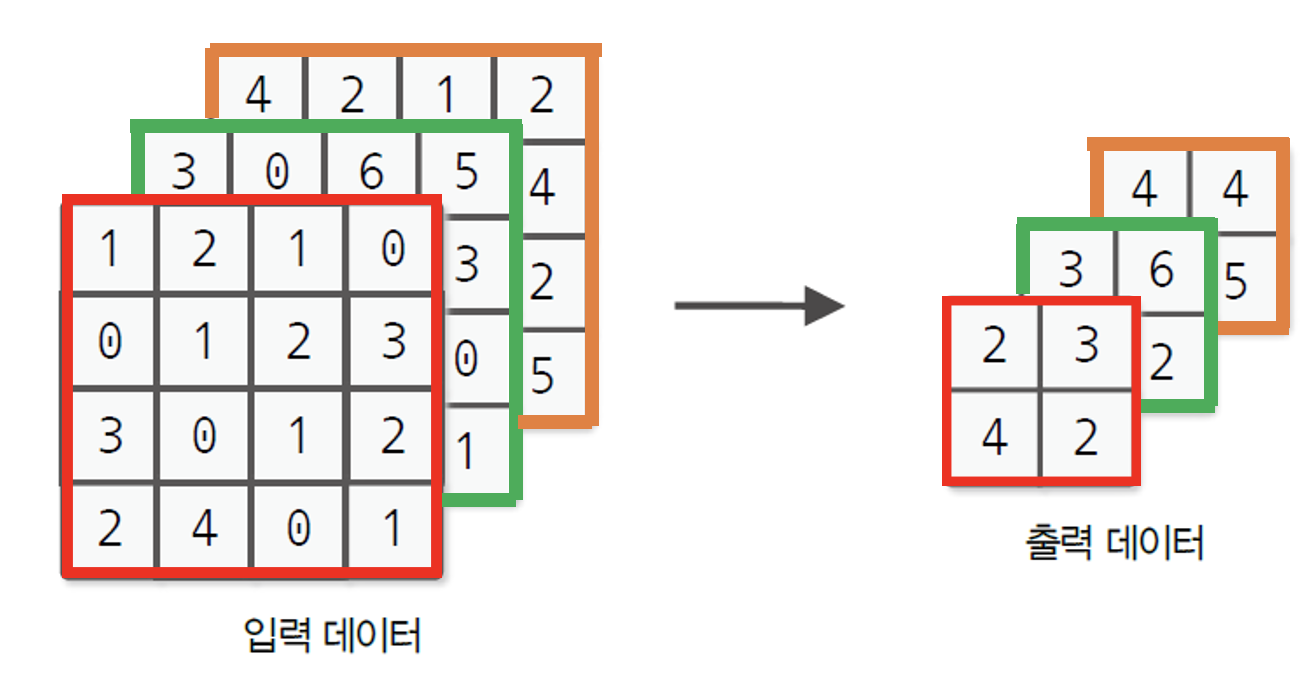
마지막으로는 미세한 위치 변화에 영향을 덜 받는다는 특징이 있다. 이 점이 잘 이해가 안 갈 수 있다. 예를 들어, 다음과 같이 두 개의 입력 이미지가 있고, 이미지의 데이터(픽셀)를 표시하면 아래와 같다.

1,2번 모두 다람쥐 이미지이다. 하지만 두 그림의 각 왼쪽 면을 자세히 살펴보면 1번은 이미지 왼쪽 끝에 다람쥐 꼬리가 맞닿아 있고, 2번은 이미지 왼쪽 끝과 다람쥐 꼬리 간에 간격이 어느정도 존재한다. 결국 1,2번 이미지는 서로 살짝 미세하게 위치가 다른 이미지라고 할 수 있다.
이러한 2개의 이미지의 픽셀 데이터를 살펴보자. 보면 1번의 픽셀값을 오른쪽으로 1칸 씩 모두 이동시킨 게 2번의 픽셀값이다. 하지만 두 픽셀 값이 서로 1칸씩 차이가 남에도 불구하고 Max Pooling 결과를 취한 값은 동일한 것을 알 수 있다.
물론 위 예시가 애초에 동일한 이미지의 데이터 간에 비교한 것이 극단적일 수 있지만, 다른 경우에는 서로 다른 이미지 이지만 비슷한 특성을 갖고 있기 때문에 풀링 결과가 동일할 수 있다. 그렇다면 이러한 효과가 시사하는 바가 무엇일까? 바로 비슷한 이미지들 즉, 픽셀값 위치가 차이가 크지 않은 여러 이미지들에 대해서 풀링으로 인해 비슷한 특징을 추출할 수 있게 되고 이는 비슷한 이미지들에 대해서 모델이 비슷한 예측값을 내뱉도록 할 것이다. 결과적으로 모델의 예측 정확성, 더 구체적으로는 모델의 오버피팅을 억제하는 효과가 있을 것이다.
지금까지 CNN을 구현하기 위한 메커니즘 모두를 살펴보았다. 이제 위 메커니즘을 우리가 키워온(?) Dezero로 어떻게 구현해볼 수 있을지 코드로 공부해보도록 하자.
3. 컨볼루션과 풀링 구현하기 - conv2d 와 pooling 함수
컨볼루션을 구현하기 위해서는 이미지 데이터를 열(Column)으로 변환하는 기능을 하는 편의함수를 활용하면 연산 속도가 빨라지기 때문에 해당 기능의 함수를 활용할 것이다. 만약 이를 활용하지 않으면 for loop 구문을 겹겹이 사용해야 하고 넘파이에서는 for loop를 사용하면 속도가 느려지는 문제가 발생한다. 함수 이름은 im2col 로 "image to column" 즉, 이미지를 열로 변환한다는 의미를 담고 있다. 그러면 대체 im2col 이라는 함수가 어떻게 이미지를 열로 변환시키는지를 이해해보자.
im2col의 목적은 입력 데이터를 한 줄로 전개함으로써 합성곱 연산 중 커널 계산에 편리하도록 입력 데이터를 펼치는 역할을 한다. 먼저 아래 그림을 살펴보자.
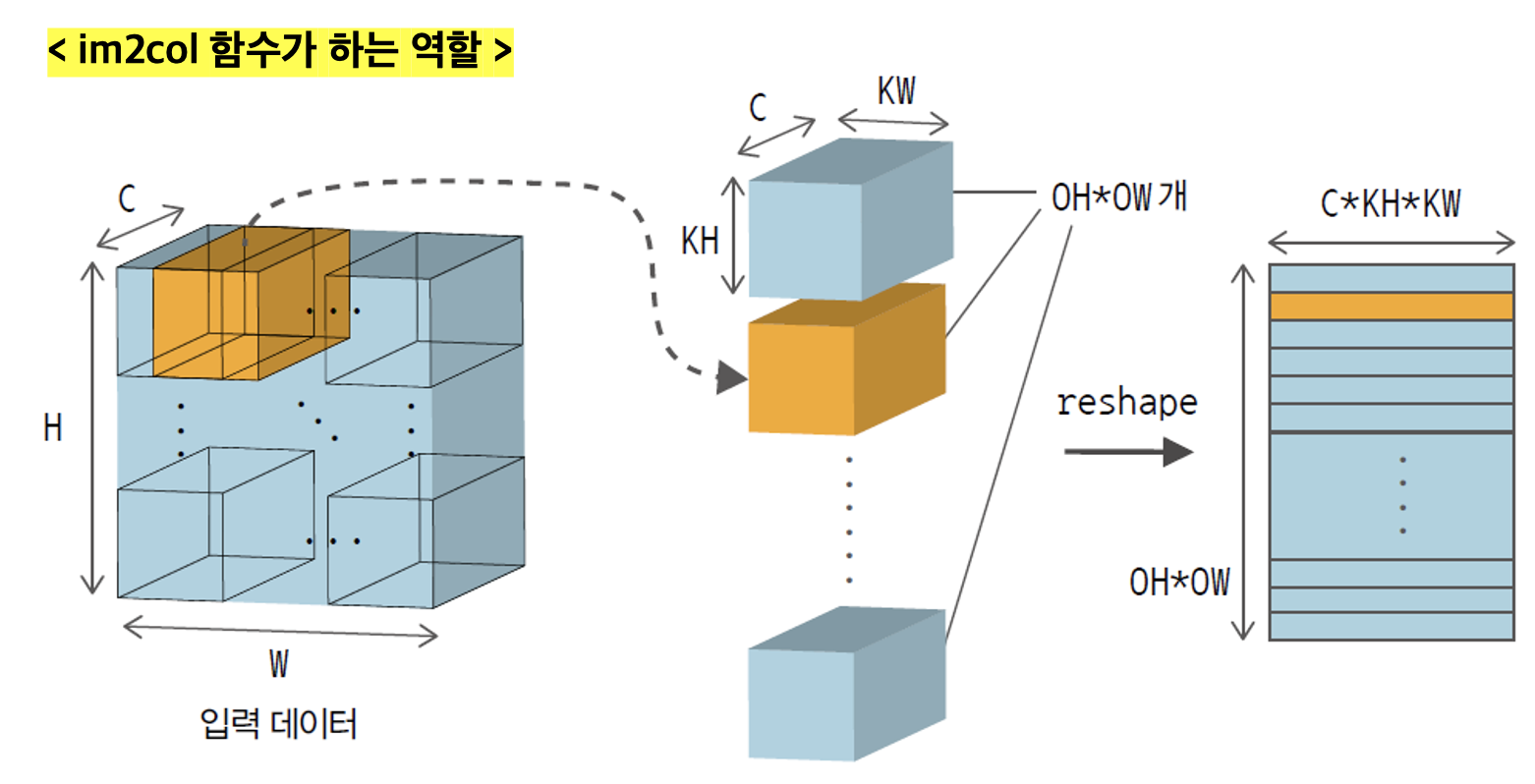
위 그림을 보면 가장 왼쪽의 입력 데이터를 특정 크기의 직육면체로 나눈 것 같은 모습을 볼 수 있다. 이 때, 직육면체의 크기(형상)은 바로 입력 데이터에 적용시킬 커널의 사이즈이다.(위 그림 상으론 커널의 형상은 (C, KH, KW) 이며 1개 커널에 대한 형상이다) 즉, 커널이 슬라이딩 윈도우를 진행하면서 연산이 수행될 입력 데이터의 부분 부분을 미리 추출해놓는 것이다. 입력 데이터의 부분 부분에 해당하는 것들이 그림의 가운데에 있는 여러 직육면체들이다. 그리고 이 여러 직육면체 각각을 2차원 형태의 행벡터로 쭉 전개(flatten) 시켜준 것이 그림의 가장 오른쪽 모습이 된다.
이렇게 im2col 함수를 사용하게 되면 가장 오른쪽 그림처럼 커널이 적용될 입력 이미지 데이터들이 2차원 형태로 전개된다. 이것이 바로 im2col 함수가 하는 역할이다. 참고로 체이너 프레임워크의 im2col 함수는 위 과정에서 가운데 단계까지만 수행해준다고 한다. 왜냐하면 입력 데이터의 부분 부분을 꺼낸 후 텐서 곱을 해서 원하는 계산을 수행할 수 있기 때문이다. 이 책에서는 행렬 곱을 수행해주는 로직으로 되어 있기 때문에 reshape까지 해줘야 한다. 추후 로직에서 알게 되겠지만 reshape 단계까지 수행할지는 특정 옵션으로 제어할 수 있도록 구현할 예정이다.
이제 im2col 함수로 입력 데이터를 전개해놓았으니 커널과 연산을 수행해야 한다. 그런데 1,2번 목차에서 배웠다시피 커널도 종류를 여러개로 해서 적용시키는 경우가 보통이다. 이럴 경우 im2col 함수를 사용한 후의 입력 데이터와 여러개의 커널 간에 컨볼루션 연산이 어떻게 수행되는지 아래 그림을 통해 알아보자.
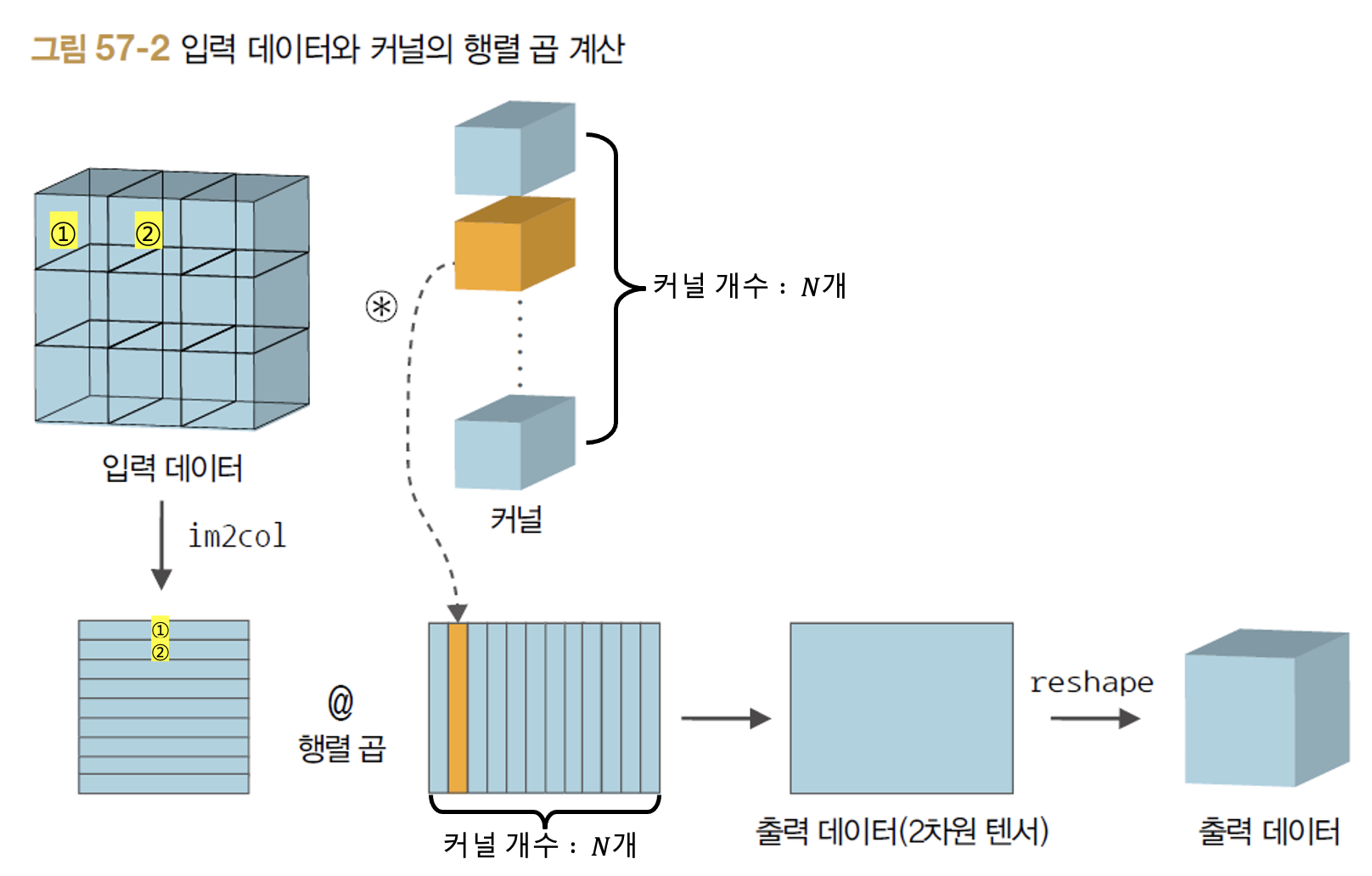
위 그림을 보면 2차원으로 변환된 입력 데이터가 행 벡터의 모음으로, 여러개의 커널들이 열 벡터의 모음으로 각각 변환하고 이 두 개의 2차원 행렬을 서로 곱해주면 출력 데이터가 만들어지는 것을 알 수 있다. 이렇게 행렬 연산을 수행하게 되면 모든 커널 각각이 입력 데이터의 모든 부분 부분과의 컨볼루션 연산을 1번씩 수행하는게 가능하다는 것을 알 수 있다.
해당 책에서는 im2col 코드를 라인 바이 라인으로 직접 설명하지는 않는다. im2col 코드는 여기를 참조하도록 하자. 책에서는 im2col 함수의 사용법과 컨볼루션 함수에 대해 집중적으로 다룬다.(im2col 함수를 동일한 기능을 하되 클래스 형태로도 구현해놓았으며 역전파 미분도 가능하도록 코드가 작성되어 있는 상태이다. 따라서 추후에 컨볼루션 역전파를 수행할 때도 정상 동작한다)
먼저 im2col 함수 사용법에 대해 간단히 알아보자. 아래와 같은 코드가 있다고 가정하자.
import numpy as np
import dezero.functions as F
x1 = np.random.rand(1, 3, 7, 7) # shape: (N, C, H, W)
col1 = F.im2col(x1, kernel_size=5, stride=1, pad=0, to_matrix=True)
print(col1.shape) # (9, 75)
x2 = np.random.rand(10, 3, 7, 7) # shape: (N, C, H, W)
col2 = F.im2col(x2, kernel_size=5, stride=1, pad=0, to_matrix=True)
print(col2.shape) # (90, 75) = (9 * 10, 75)
위와 같이 예시 입력 데이터가 있을 경우, im2col 함수를 사용했을 때 어떻게 2차원 형태로 전개되는지는 주석을 살펴보자. 그러면 이제 컨볼루션을 구현하는 conv2d_simple 이라는 함수를 구현시켜보도록 하자. 여기에서 im2col 함수로 입력 데이터를 2차원으로 전개해주고, 또 여러개의 커널도 2차원으로 전개해준 후, 두 행렬에 대한 선형(Linear) 연산을 취해주도록 한다.
from dezero import as_variable
from dezero.functions import linear
from dezero.utils import pair, get_conv_outsize
def conv2d_simple(x, W, b=None, stride=1, pad=0):
x, W = as_variable(x), as_variable(W)
Weight = W
N, C, H, W = x.shape
OC, C, KH, KW = Weight.shape
SH, SW = pair(stride)
PH, PW = pair(pad)
OH = get_conv_outsize(H, KH, PH, SH)
OW = get_conv_outsize(W, KW, PW, SW)
# convert image to 2d-array(row vector)
col = im2col(x, (KH, KW), stride, pad, to_matrix=True)
# convert filter(all kernel) to 2d-array(column-vector)
Weight = Weight.reshape(OC, -1).transpose()
t = linear(col, Weight, b)
y = t.reshape(N, OH, OW, OC).transpose(0, 3, 1, 2)
return y
위 함수를 사용하는 예시는 아래와 같다. 정상적으로 동작하는 것을 볼 수 있다.
import numpy as np
from dezero import Variable
import dezero.functions as F
N, C, H, W = 1, 5, 15, 15
OC, (KH, KW) = 8, (3, 3)
x = Variable(np.random.rand(N, C, H, W))
W = np.random.rand(OC, C, KH, KW)
y = F.conv2d_simple(x, W, b=None, stride=1, pad=1)
y.backward(use_heap=True)
print(y.shape) # (1, 8, 15, 15)
print(x.grad.shape) # (1, 5, 15, 15)
참고로 conv2d_simple 함수는 im2col로 전개한 입력 데이터를 메모리에서 즉시 삭제하지 않고 계속 갖고 있는다. 따라서 이러한 메모리 소모를 줄이기 위해서 클래스 계층으로 만든 코드도 존재한다. 해당 코드는 원본 코드를 참조하도록 하자.
그러면 이제 위 함수들을 기반으로 2차원 컨볼루션 계층(Conv2d)을 만들어보도록 하자. 이전에 구현했던 선형 연산(Linear) 계층과 구현 동작 방식은 비슷하다. 아래에 기반해서 여러가지 컨볼루션 계층은 이후 목차인 VGG16 모델을 만들 때 사용해보도록 하자.
import os
import weakref
import numpy as np
from dezero import Parameter
from dezero import functions as F
from dezero.utils import pair
class Conv2d(Layer):
def __init__(self, out_channels, kernel_size, stride=1, pad=0,
nobias=False, dtype=np.float32, in_channels=None):
super(Conv2d, self).__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.kernel_size = kernel_size
self.stride = stride
self.pad = pad
self.dtype = dtype
self.W = Parameter(None, name='W')
if in_channels is not None:
self._init_W()
if nobias:
self.b = None
else:
self.b = Parameter(np.zeros(out_channels, dtype=dtype), name='b')
def _init_W(self, xp=np):
C, OC = self.in_channels, self.out_channels
KH, KW = pair(self.kernel_size)
scale = np.sqrt(1 / (C * KH * KW))
W_data = xp.random.rand(OC, C, KH, KW).astype(self.dtype) * scale
self.W.data = W_data
def forward(self, x):
if self.W.data is None:
self.in_channels = x.shape[1] # `x` shape must be (N, C, H, W)
self._init_W()
y = F.conv2d_simple(x, self.W, self.b, self.stride, self.pad)
return y
마지막으로 pooling 함수를 구현할 차례다. 풀링도 마찬가지로 im2col 함수를 사용한다. 하지만 알다시피, 풀링은 선형 연산은 적용하지 않는다. 한 가지 주의할 점은 Max 또는 Average 등 풀링을 적용할 때 각 채널마다 독립적으로 수행해준다는 점이다. 풀링을 im2col 을 활용해 수행하는 방법을 도식화하면 아래와 같다.
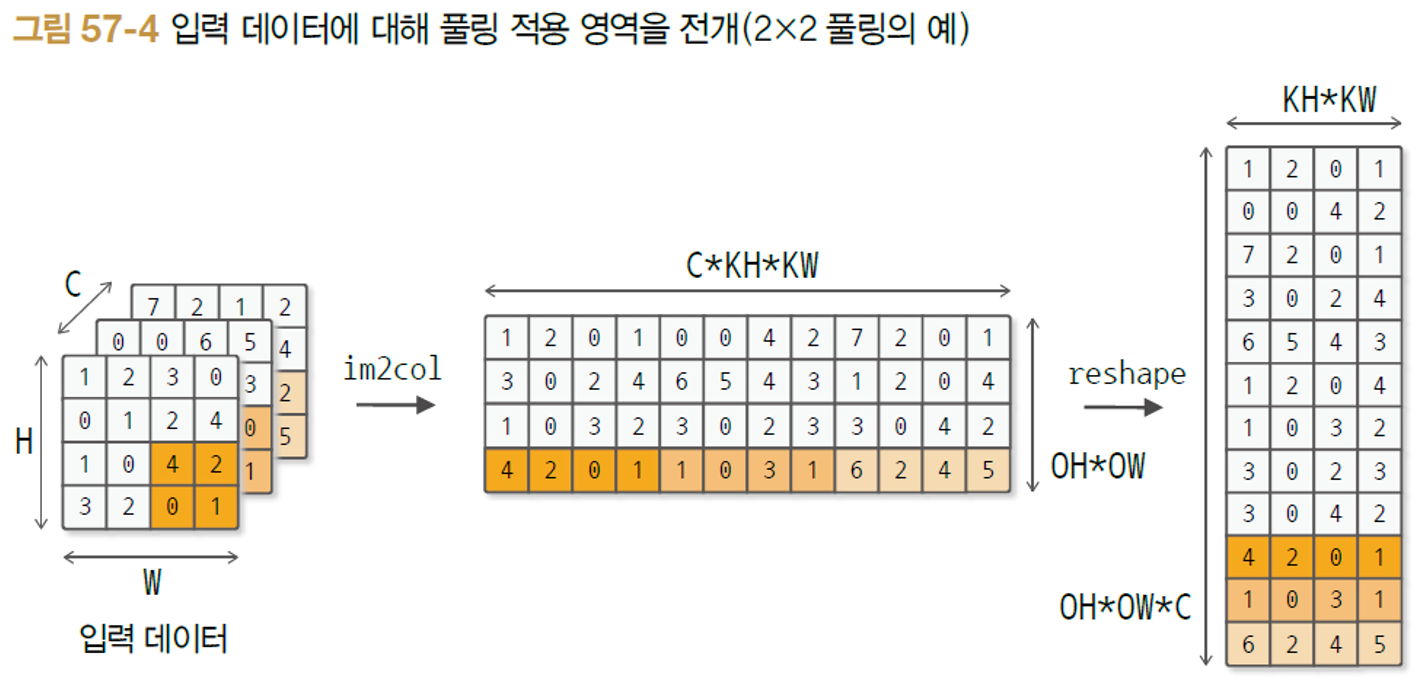
위 과정을 im2col로 입력 데이터를 2차원으로 전개한 후, reshape한 과정까지를 나타낸다. 가장 맨 오른쪽 그림에서 이제 Max 값만을 골라주면 되는데, 색칠한 것에서 눈치챌 수 있다시피 행 방향(axis=1)으로 최대값 요소만 추출하면 Max pooling을 수행할 수 있게 된다. 그리고 마지막으로 출력 데이터를 입력 데이터처럼 3차원 형상으로 reshape 해주면 된다.
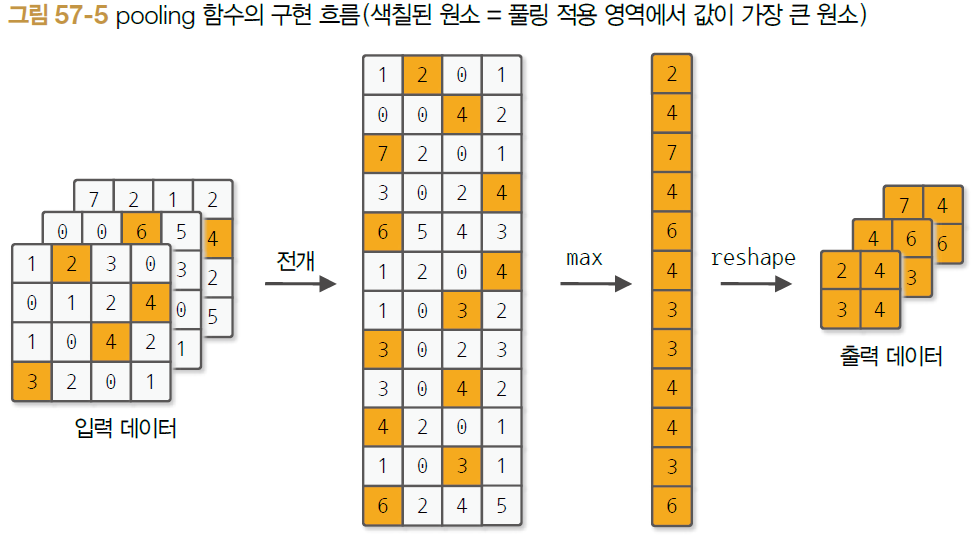
Max Pooling을 코드로 구현한 함수는 아래와 같다.
from dezero import as_variable
from dezero.functions import linear
from dezero.utils import pair, get_conv_outsize
def pooling_simple(x, kernel_size, stride=1, pad=0):
x = as_variable(x)
N, C, H, W = x.shape
KH, KW = pair(kernel_size)
SH, SW = pair(stride)
PH, PW = pair(pad)
OH = get_conv_outsize(H, KH, PH, SH)
OW = get_conv_outsize(W, KW, PW, SW)
col = im2col(x, kernel_size, stride, pad, to_matrix=True)
col = col.reshape(-1, KH * KW)
y = col.max(axis=1)
y = y.reshape(N, OH, OW, C).transpose(0, 3, 1, 2)
return y
지금까지 배운 내용들을 기반으로 VGG16 모델을 구현하고 테스트하는 코드는 깃헙을 참고하도록 하자.
4. 시계열 데이터 처리에 적합한 RNN
이번 목차에서는 보다 시계열 처리에 적합하다고 알려져 있는 RNN 모델을 Dezero 프레임워크를 활용해 빌드해보도록 하자. RNN은 순환 구조라는 특성 때문에 입력만 출력에 영향을 미치는 FNN과는 달리 입력과 '은닉 상태'라는 추가적인 값이 출력에 영향을 주게 된다. 이번 포스팅에서는 RNN에 대한 이론적인 측면보다 구현하는 것에 초점을 맞춘다. RNN에 대한 이론은 시리즈 책 2권의 포스팅에 자세히 나와있으므로 해당 포스팅을 참조하도록 하자.
우선 RNN의 은닉상태 $h_t$를 만드는 순전파 수식부터 살펴보자.
$$h_t = tanh(h_{t-1}W_h + x_tW_x + b)$$
이 때, $t$는 시간(시점)을 의미한다. 위 수식을 보면 RNN은 특이하게 가중치가 2개인 것을 알 수 있다. 하나는 입력 $x_t$를 은닉 상태 $h_t$로 변환하기 위한 가중치 $W_x$이다. 반면에 다른 것은 이전 RNN의 출력인 $h_{t-1}$을 다음 시각 $t$의 출력($h_t$)으로 변환하기 위한 가중치 $W_h$이다. 마지막으로는 편향 $b$가 존재한다. 참고로 여기서 $h_{t-1}, x_t$는 행 벡터이고 $W_h, W_x$는 열 벡터이다.
위 수식을 참고해서 RNN 이라는 계층을 만들어보자. RNN이라고 해서 특별하게 따로 구현할 계층은 없다. 우리가 기존에 만들어온 Linear 계층과 여러가지 함수들을 활용해서 구현하면 된다. 아래 코드는 RNN 계층 코드이다.
class RNN(Layer):
def __init__(self, hidden_size, in_size=None):
super(RNN, self).__init__()
# 수식 x_t * W_x + b 을 구현
self.x2h = Linear(out_size=hidden_size, in_size=in_size)
# 수식 h_t-1 * W_h 을 구현
self.h2h = Linear(out_size=hidden_size, in_size=in_size, nobias=True)
self.h = None # RNN 계층의 출력값 캐싱
def reset_state(self):
self.h = None
def forward(self, x):
if self.h is None:
h_new = F.tanh(self.x2h(x))
else:
h_new = F.tanh(self.x2h(x) + self.h2h(self.h))
self.h = h_new
return h_new
위 수식을 코드로 그대로 구현하면 위와 같이 된다. 코드에서 순전파 시 즉, forward() 메소드를 실행할 때 한 가지 주의할 점이 있다. 바로 RNN이 최초로 시작할 때에는 이전 RNN 계층이 없기 때문에 은닉 상태가 없는 상태(None 값)일 수 밖에 없다. 따라서 은닉 상태가 있냐 없냐에 따라 if 구문 분기를 활용해서 순전파를 진행해주도록 한다.
그러면 시계열 데이터가 있을 때, 데이터 하나 하나씩 입력될 때마다 위 RNN의 순전파를 진행하면서 그려지는 계산 그래프 형태는 어떻게 될까? 먼저 최초 입력 데이터 1개를 RNN 계층에 넣었을 경우에 계산 그래프는 아래와 같아진다.
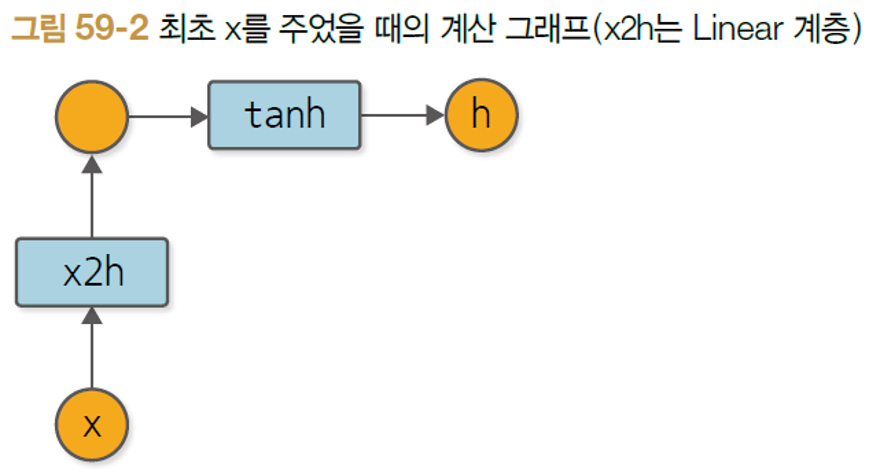
그러면 두 번째 데이터가 입력되었을 경우에 순전파 계산 그래프는 어떻게 확장될까? 이해하기 쉽도록 아래 계산 그래프 단계 마다 수식을 적어놓았다. 수식과 같이 이해하면 계산 그래프의 동작 과정도 이해하기 수월할 것이다.
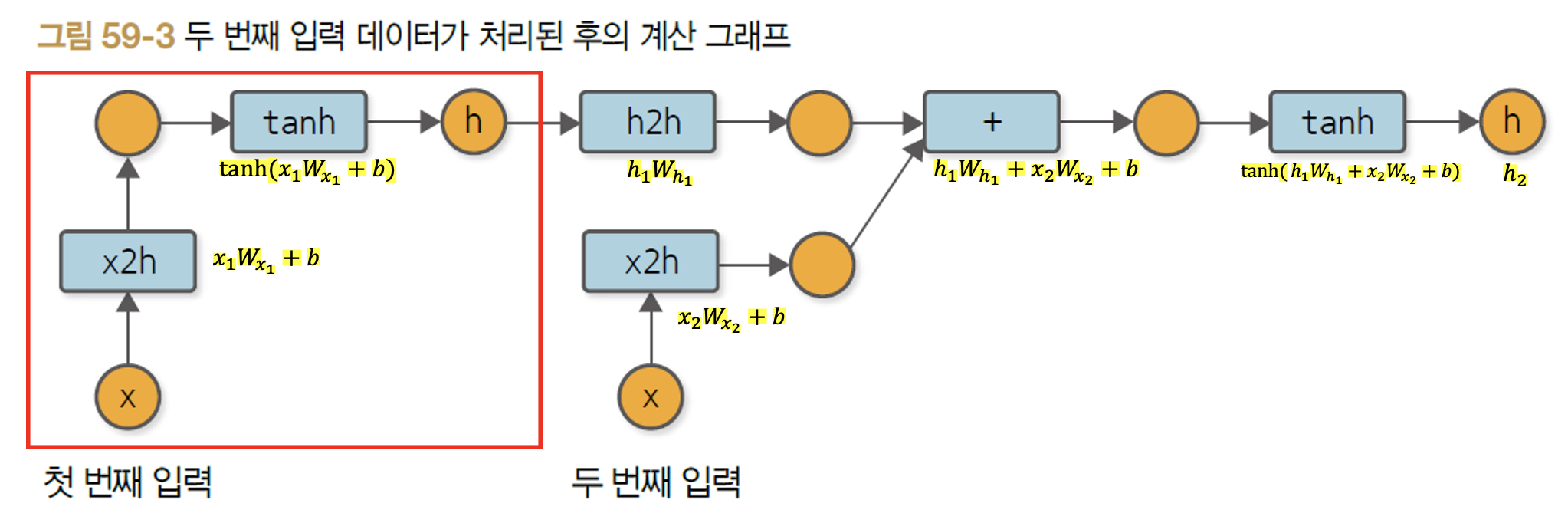
참고로 여기서 주의해야 할 점은 위 그림에서 가중치 값들($W_h, W_x$)이 1,2로 분리되어 있어서 다른 값이라고 생각할 수 있지만, 동일한 값들임이다. 즉, $W_{x_1}$과 $W_{x_2}$는 별도로 존재하는 파라미터가 아닌 하나의 동일한 파라미터이며 다른 것은 파라미터 '값' 자체만 다른 셈이다. 이에 대해서 이해가 잘 가지 않는다면 예전 포스팅 [2.순환신경망(RNN)] 목차의 글을 살펴보도록 하자.
그러면 이제 위에서 구현한 RNN 계층을 활용해서 간단한 신경망 모델을 구축해보도록하자. 방금 구현한 RNN 계층이 출력시킨 최종 은닉 상태 값에 Fully Connected Layer(Linear 계층) 하나만 추가해서 최종 출력값이 되도록 해보자.
from dezero import Model
import dezero.layers as L
class SimpleRNN(Model):
def __init__(self, hidden_size, out_size):
super(SimpleRNN, self).__init__()
self.rnn = L.RNN(hidden_size)
self.fc = L.Linear(out_size)
def reset_state(self):
self.rnn.reset_state()
def forward(self, x):
h = self.rnn(x)
y = self.fc(h)
return y
그리고 위 코드를 활용해서 아래처럼 입력 데이터 2번째까지 들어갔을 때 역전파를 시도해보도록 하자. 이렇게 하는 이유는 RNN의 역전파 방법인 (Truncated) BPTT 방식을 이해하기 위함이다.
import numpy as np
seq_data = [np.random.randn(1, 1) for _ in range(1000)]
xs = seq_data[:-1]
ts = seq_data[1:]
model = SimpleRNN(10, 1)
loss, cnt = 0, 0
for x, t in zip(xs, ts):
y = model(x)
loss += F.mean_squared_error(y, t)
cnt += 1
if cnt == 2:
model.clear_grads()
loss.backward()
break
2번째 입력 데이터까지 순전파를 진행하고 난 뒤 역전파를 수행했을 때의 계산 그래프는 아래와 같다.
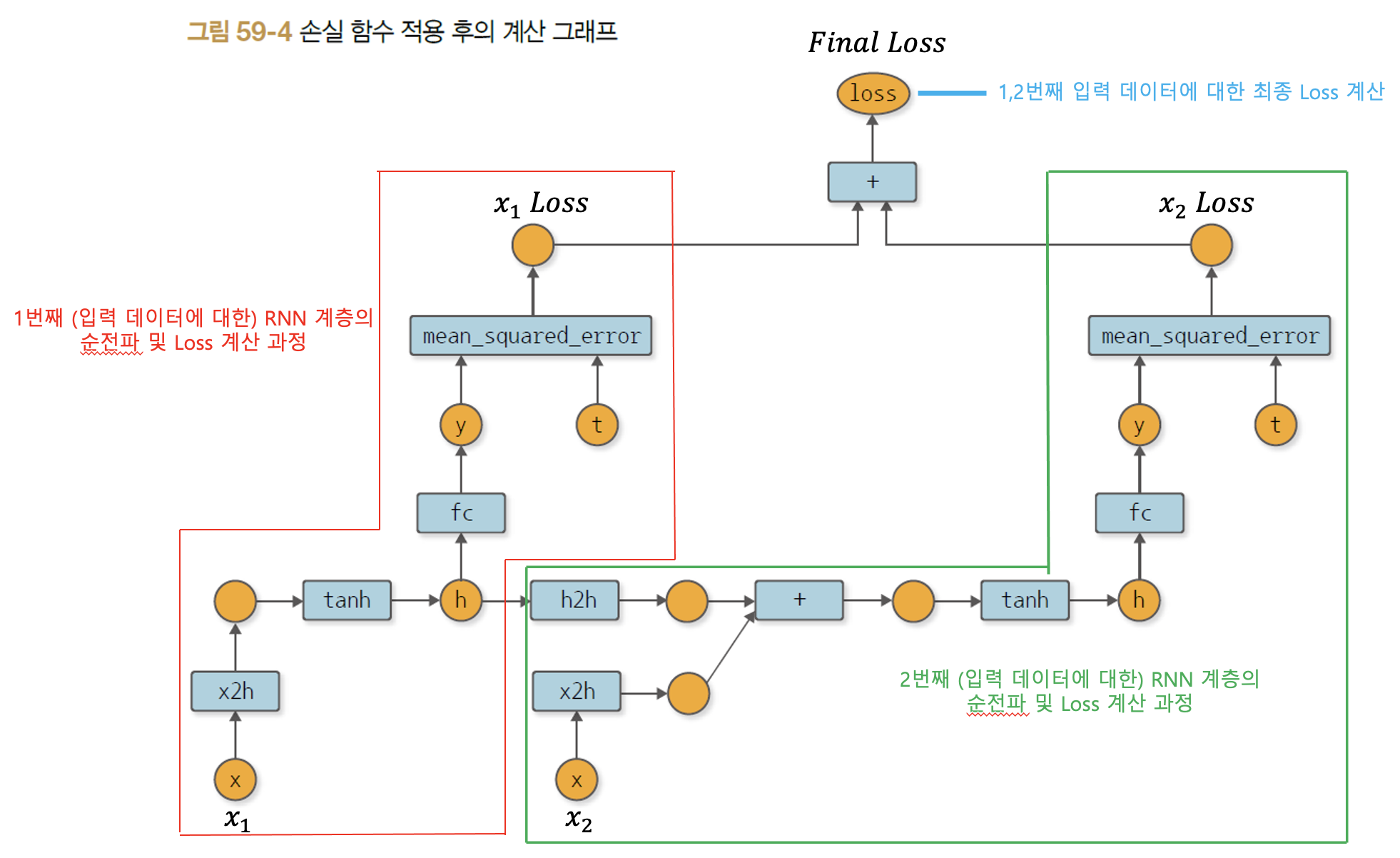
시계열 데이터가 입력됨에 따라 RNN 계층에서 만들어지는 순전파 계산 그래프는 위처럼 그려진다. 그리고 위 계산 그래프에서 이제 역전파를 수행하게 되고 이를 BPTT 방법이라고 한다. 그런데 위처럼 2개의 입력 데이터에 대해서는 문제가 없겠지만, 시계열 데이터가 길어짐에 따라 계속 계산 그래프가 확장되면 역전파 시 기울기 소실 문제가 발생하게 된다. 그래서 엄청나게 길어진 계산 그래프를 역전파 시 중간에 '끊어주는' Truncated BPTT가 해결책으로 등장한다. 이러한 RNN의 역전파 과정에 대한 세부적인 이론은 예전 포스팅 [3.RNN의 오차역전파, BPTT와 Truncated BPTT] 목차를 참조하도록 하자.
Truncated BPTT를 수행할 때 주의할 점은 계산 그래프를 잘라내는 것을 역전파에만 수행해야 한다는 것이다. 즉, 순전파 시에는 계산 그래프를 자르지 않아야 한다. 왜냐하면 역전파 시에 사용할 은닉상태 값을 순전파 시에 생성하기 때문이다.
그러면 Truncated BPTT를 구현하기 위해서는 계산 그래프의 연결을 끊어주는 메서드가 필요하다. 구현은 간단하다.
class Variable:
...(생략)...
def unchain(self):
self.creator = None
바로 Variable 인스턴스의 창조자 즉, 해당 Variable 인스턴스를 만들어낸 함수를 초기화시키는 것이다. 이는 우리가 최초에 Variable 클래스에 역전파를 과정을 구현했던 것을 상기시켜보면 쉽게 이해할 수 있다. 우리는 특정 Variable 인스턴스마다 그 인스턴스의 창조자 함수가 None 값이 아닐 경우에 역전파를 진행시키도록 했다. 이 말은 즉슨, 창조자 함수가 None으로 설정되면 언제든지 역전파 과정이 중지된다는 뜻이다.
이제 그러면 위 추가된 unchain 이라는 메서드가 호출된 변수를 기준으로 시작해서 계산 그래프를 거슬러 올라가면서(역전파 방향으로) 마주치는 모든 변수의 창조자 함수를 초기화시켜주도록 한다. 이 기능을 수행하는 메서드가 unchain_backward() 라는 아래의 메소드다.
class Variable:
...(생략)...
def unchain(self):
self.creator = None
def unchain_backward(self):
if self.creator is not None:
funcs = [self.creator]
while funcs:
f = funcs.pop()
for x in f.inputs:
if x.creator is not None:
funcs.append(x.creator)
x.unchain()
그러면 이제 간단한 더미 시계열 데이터셋으로 단순한 RNN 신경망을 순전파 시키면서 Truncated BPTT 역전파도 적용해보자. 그리고 각 학습마다 Loss가 줄어드는지도 관찰해보자.
import dezero
from dezero.models import SimpleRNN
from dezero.optimizers import Adam
from dezero import functions as F
max_epoch = 100
hidden_size = 100
bptt_length = 30
train_set = dezero.datasets.SinCurve(train=True)
seqlen = len(train_set)
model = SimpleRNN(hidden_size, 1)
optimizer = Adam().setup(model)
for epoch in range(max_epoch):
model.reset_state() # epoch 마다 RNN 은닉상태값들 초기화
loss, bptt_cnt = 0, 0
for x, t in train_set:
# predict and loss
x = x.reshape(1, 1) # 2차원 shape로 변경해주기
y = model(x)
loss += F.mean_squared_error(y, t)
bptt_cnt += 1
# Truncated BPTT
if bptt_cnt % bptt_length == 0 or bptt_cnt == seqlen:
model.clear_grads() # 1. BPTT 또 수행할 때는 이전에 갱신해놓은 기울기 초기화해야지!
loss.backward() # 2. ~현재 변수까지 시간을 거슬러 역전파 수행
loss.unchain_backward() # 3. BPTT 수행할 때는 지금 변수까지의 창조자 함수 없애버리기!
optimizer.update() # 4. 기울기 갱신
avg_loss = float(loss.data) / bptt_cnt
print('Epcoh:', epoch, '-> AVG Loss:', avg_loss)
Truncated BPTT를 수행할 때 크게 4가지 단계를 수행한다. 먼저 순차적으로 시계열 데이터가 입력된다고 가정 했을 때, 사전에 설정한 끊을 주기마다 아래 4단계를 반복한다.
- 또 다른 BPTT 주기가 왔을 때, 이전에 BPTT로 갱신해놓은 기울기를 초기화(for 기울기 소실을 막기 위함이 Truncated의 목적이니깐)
- 특정 변수부터 현재 변수까지의 BPTT 역전파 수행
- BPTT 역전파를 수행한 변수들의 창조하 함수를 초기화(for 다음 주기의 BPTT를 수행할 떄, 앞단의 변수까지 가지 않도록 하기위함)
- 기울기 갱신
위 과정까지는 시계열 데이터를 입력시키는 단위가 1개일 때를 적용한 셈이다. 시계열 데이터도 미니 배치 단위로 적용할 수 있다. 다음 목차에서는 미니 배치 단위의 시계열 데이터에도 적용시키도록 확장하는 방법을 공부해보자.
5. 미니 배치의 시계열 단위까지의 확장, 그리고 LSTM 활용
이번엔 크게 2가지를 배워볼 것이다. 첫 번째는 시계열 데이터를 1개가 아닌 이제 N개의 묶음 단위로 미니배치 처리할 수 있도록 시계열 데이터 전용의 데이터로더를 만들어보는 것, 두 번째는 기존 RNN의 한계점을 극복하는 게이트가 추가된 LSTM 을 만들어보는 것.
먼저 시계열 데이터 전용의 데이터로더를 만들어보자. 시계열 데이터를 미니배치로 처리하려면 데이터를 뽑는 시작 위치를 배치별로 다르게 하면 된다. 예를 들어, 1만개의 시계열 데이터가 있다고 가정했을 때 배치 사이즈가 5,000이라고 해보자. 그러면 총 2개의 미니 배치가 나오게 되는데, 첫 번째 미니배치의 시작 위치는 0번째일 것이고, 두 번째 미니배치 데이터의 시작 위치는 5,000번째일 것이다. 이런 원리를 염두에 두고 데이터 로더를 만들어보자.(참고로 아래 코드에서 상속받은 DataLoader 클래스는 이전 포스팅 6번 목차에서 구현했던 것이므로 설명은 생략하겠다.)
class SeqDataLoader(DataLoader):
def __init__(self, dataset, batch_size):
super(SeqDataLoader, self).__init__(dataset, batch_size, shuffle=False)
def __next__(self):
if self.iteration >= self.max_iter:
self.reset()
raise StopIteration
jump = self.data_size // self.batch_size
batch_index = [(i * jump + self.iteration) % self.data_size for i in range(self.batch_size)]
batch = [self.dataset[i] for i in batch_index]
x = np.array([ex[0] for ex in batch])
t = np.array([ex[1] for ex in batch])
self.iteration += 1
return x, t
위 코드에서 주의해야 할 점은 shuffle 기 False로 무조건 디폴트 인자여야 한다. 왜냐하면 시계열 데이터는 시퀀스 데이터이기 때문에 데이터의 순서가 뒤바뀌어서는 안되기 때문이다.
다음은 두번째로 구현할 LSTM 계층이다. LSTM 계층에 대한 수식은 아래와 같다. LSTM에 대한 자세한 이론은 예전 책2권 포스팅을 참조하도록 하자.
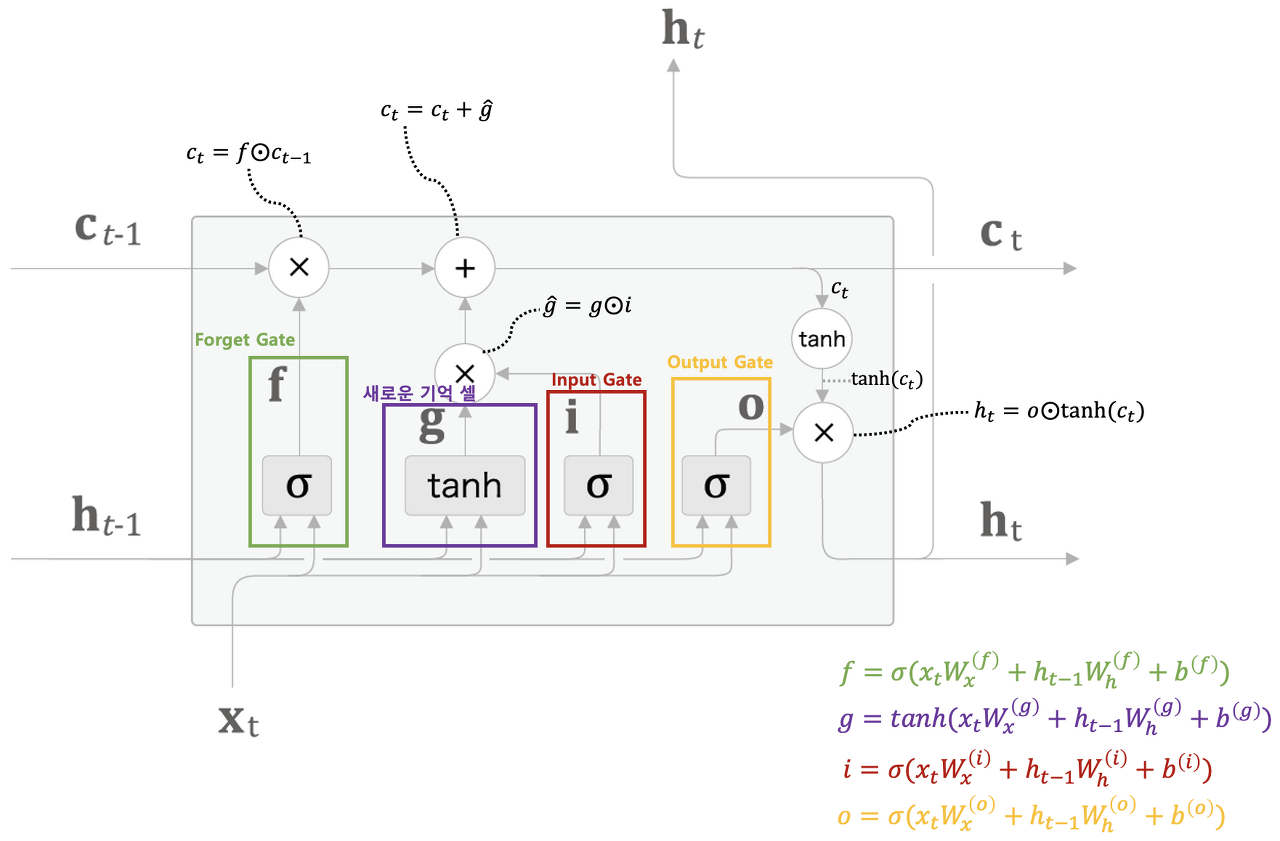
위 수식을 토대로 LSTM 계층을 코드로 구현하면 아래와 같다.
class LSTM(Layer):
def __init__(self, hidden_size, in_size=None):
super(LSTM, self).__init__()
H, I = hidden_size, in_size
# Forget gate
self.x2f = Linear(H, in_size=I)
self.h2f = Linear(H, in_size=H, nobias=True)
# Output gate
self.x2o = Linear(H, in_size=I)
self.h2o = Linear(H, in_size=H, nobias=True)
# Input gate
self.x2i = Linear(H, in_size=I)
self.h2i = Linear(H, in_size=H, nobias=True)
# Main gate
self.x2g = Linear(H, in_size=I)
self.h2g = Linear(H, in_size=H, nobias=True)
self.reset_state()
def reset_state(self):
self.c = None
self.h = None
def forward(self, x):
if self.h is None:
f = F.sigmoid(self.x2f(x))
o = F.sigmoid(self.x2o(x))
i = F.sigmoid(self.x2i(x))
g = F.tanh(self.x2g(x))
else:
f = F.sigmoid(self.x2f(x) + self.h2f(self.h))
o = F.sigmoid(self.x2o(x) + self.h2o(self.h))
i = F.sigmoid(self.x2i(x) + self.h2i(self.h))
g = F.tanh(self.x2g(x) + self.h2g(self.h))
# 기억 셀
if self.c is None:
c_new = g * i
else:
c_new = (g * i) + (self.c * f)
# 은닉 상태
h_new = F.tanh(c_new) * o
self.c, self.h = c_new, h_new
return h_new
그러면 위 LSTM 계층을 활용해서 더미 데이터를 활용해서 1개의 히스토리컬 데이터를 가지고 1개의 미래 스텝을 예측하는 단일 스텝모델을 아래처럼 만들어보자.
import dezero.layers as L
class BetterRNN(Model):
def __init__(self, hidden_size, out_size):
super(BetterRNN, self).__init__()
self.lstm = L.LSTM(hidden_size)
self.fc = L.Linear(out_size)
def reset_state(self):
self.lstm.reset_state()
def forward(self, x):
x = self.lstm(x)
y = self.fc(x)
return y
위처럼 LSTM 계층 1개를 쌓고 Fully Connected Layer를 1개 쌓은 BetterRNN 이라는 이름의 모델을 활용해서 더미 데이터에 대한 학습을 수행해보도록 하자. 코드는 아래와 같다.
import dezero.functions as F
from dezero.datasets import SinCurve
from dezero.dataloaders import SeqDataLoader
from dezero.models import BetterRNN
from dezero.optimizers import Adam
max_epoch = 100
batch_size = 30
hidden_size = 100
bptt_length = 30
train_set = SinCurve(train=True)
train_loader = SeqDataLoader(train_set, batch_size)
seqlen = len(train_set)
model = BetterRNN(hidden_size, out_size=1)
optimizer = Adam().setup(model)
for epoch in range(max_epoch):
model.reset_state() # reset state per each epoch
loss, bptt_cnt = 0, 0
for x, t in train_loader:
# predict and get loss
y = model(x)
loss += F.mean_squared_error(y, t)
bptt_cnt += 1
# Truncated BPTT
if bptt_cnt % bptt_length == 0 or bptt_cnt == seqlen:
# 1. 현재 상태 기울기 초기화
model.clear_grads()
# 2. 역전파 수행
loss.backward(use_heap=True)
# 3. 다음 BPTT 대비 위해 앞단 Variable의 창조자 삭제
loss.unchain_backward()
# 4. 기울기 갱신
optimizer.update()
avg_loss = float(loss.data) / bptt_cnt
print('Epoch:', epoch, '-> Loss:', avg_loss)해당 목차를 끝으로 밑바닥부터 시작하는 딥러닝 3권의 모든 고지가 끝이났다. 3권을 읽고 첫 포스팅을 했던 시기는 2022년 4월이였고, 2권은 2021년 11월 말, 1권은 2021년 11월 초였다. 약 1년 간 책 3권을 읽으면서 많은 내용도 배웠지만 그 만큼 기초가 부족한 나의 모습을 볼 수 있었다. 뿐만 아니라 세 권의 책을 그냥 읽고 지나치는 것이 아닌 코드를 따라치며 나만의 언어로 재구성하면서 글로 기록하다 보니 이렇게 책을 깊게 소화한 적이 있었나 싶다. 지금 이 순간에서 뒤를 돌아보았을 때, 세 권의 책을 읽으면서 정말 많은 배움을 얻어온 것 같다.
최근에는 해당 책 시리즈 4권이 일본어 판으로 출판되었고 한국어 번역서를 기다리고 있는 시점이다. 4권은 강화학습에 대한 내용인 것 같았다. 벌써부터 흥미롭다. 책 4권의 한국어판이 나오기 전까지는 지금까지 배워온 3권의 내용을 다시 복습하면서 나만의 딥러닝 프레임워크를 다시 만들어보고 PyPI 같은 오픈소스 패키지 저장소에 공개해보려고 한다. 끝으로 앞으로 종류가 무엇이던 Define-by-Run 철학을 채택한 모든 딥러닝 프레임워크를 사용할 수 있는 작은 용기가 생겼다는 것에 번역저자, 원저자 분에게 깊은 감사 인사를 드린다.
'Data Science > 밑바닥부터시작하는딥러닝(3)' 카테고리의 다른 글
| [밑시딥] 나만의 딥러닝 프레임워크 만들기, 더 큰 도전으로(1) (0) | 2022.09.17 |
|---|---|
| [밑시딥] 나만의 딥러닝 프레임워크 만들기, 신경망 만들기(2) (0) | 2022.08.27 |
| [밑시딥] 나만의 딥러닝 프레임워크 만들기, 신경망 만들기(1) (0) | 2022.08.13 |
| [밑시딥] 나만의 딥러닝 프레임워크 만들기, 고차 미분 계산(2) (0) | 2022.07.09 |
| [밑시딥] 나만의 딥러닝 프레임워크 만들기, 고차 미분 계산(1) (0) | 2022.06.11 |



