이번 포스팅에는 상관계수에 대한 간단한 복습과 연합정규분포에 대해서 알아보려고 한다. 우선 저번 시간에서 다루었던 상관계수에 대해 간단하게 복습해보고 가자.
1. 상관계수에 대한 복습

상관계수를 구하기 전에 우선 공분산을 구해야 한다. 공분산은 두개의 확률변수를 각각의 확률변수에 해당하는 평균값을 빼준 값들을 곱한 후의 평균값을 의미한다. 정리하게 되면 E[XY] - mx*my 가 된다. (mx란 확률변수 X에 대한 평균값을 의미한다.)
그리고 오른쪽 그림처럼 확률변수 Y=aX+b 라는 직선으로 정의할 때 그래프를 그려봄으로써 a의 값에 따라 상관계수의 값을 알아보자. a가 양수일 때는 상관계수값이 1로 두 개의 확률변수가 같은 방향임을 알 수 있다. 반대로 상관계수가 -1일때는 두 개의 확률변수가 서로 반대의 방향임을 알 수 있다.
간단하게 키와 몸무게라는 2가지 변수로 예를 들어서 설명해보자.

위와 같이 키는 확률변수 X, 몸무게는 확률변수 Y로 정의한다. 1번 그래프를 보면 모든 X,Y에 대한 데이터를 그래프위에 나타내어 상관관계를 구하게 된다. 흥미로운 점은 2번 그래프이다. 2번 그래프의 Y축은 확률변수 X의 특정값 x일 때의 확률변수 Y일때의 조건부평균값을 이용하게 된다. 즉, X축(키)의 120cm 일 때의 모든 몸무게(Y값)의 평균 값에 해당 하는 점을 하나 찍고 다음에는 X축(키)이 130cm, 140cm, 150cm ...도 똑같이 조건부평균점을 찍어 점을 이은 뒤 상관관계를 나타낼 수도 있다.
2번의 장점은 데이터가 막대하게 많아진다면 모든 데이터를 그래프 위에 나타내는 데 시간이 오래걸릴 것이고 이 때 조건부평균을 이용하게 되면 그래프에 나타내는 시간도 줄이면서 원하는 상관관계를 얻을 수 있을 것이다.
연합정규분포에 들어가기에 앞서 다중연합 확률변수에 대해 표현하는 방식에 대해서 살펴보고 넘어가자.
<다중 연합 확률변수>

확률변수 X1~Xn까지 존재할 때 각 확률변수의 성격(이산/연속)대로 각 PDF 또는 확률에 대한 함수를 정의해줄 수 있다.
그리고 다중확률변수일 때 조건부확률을 정의해줄 수 있는데 오른쪽그림과 같이 나타내어질 수 있다. 식을 전개한 방법은 우리가 기존에 배웠던 연속확률변수일 때 Joint(연합) PDF를 함수를 구하는 방식을 이용하면 된다.
오른쪽 그림과 같은 방법은 주로 Time-Domain 사례에 사용되는데 현실에 적용되는 사례로는 미사일을 쏘아올렸을 때 미사일이 날아가는 동안의 실시간 위치를 파악하는 사례를 들 수 있다.
2. 다항분포

다항분포의 정의는 n번 시행했을 때 3가지 이상의 사건이 발생할 확률을 의미한다. 기존에 이항분포를 구하기 위해 베르누이시행과 조합을 이용한 것처럼 다항분포도 조합과 베르누이시행을 이용해 식을 세워주면 된다. 이러한 추상적인 예시가 이해하기 힘들다면 손쉬운 예시로 10개의 공 중 빨간공 4개, 파란공 3개, 초록공 3개를 일렬로 나열한다고 생각해보자.(물론 중복은 세지않는다.)
3. 연합정규분포
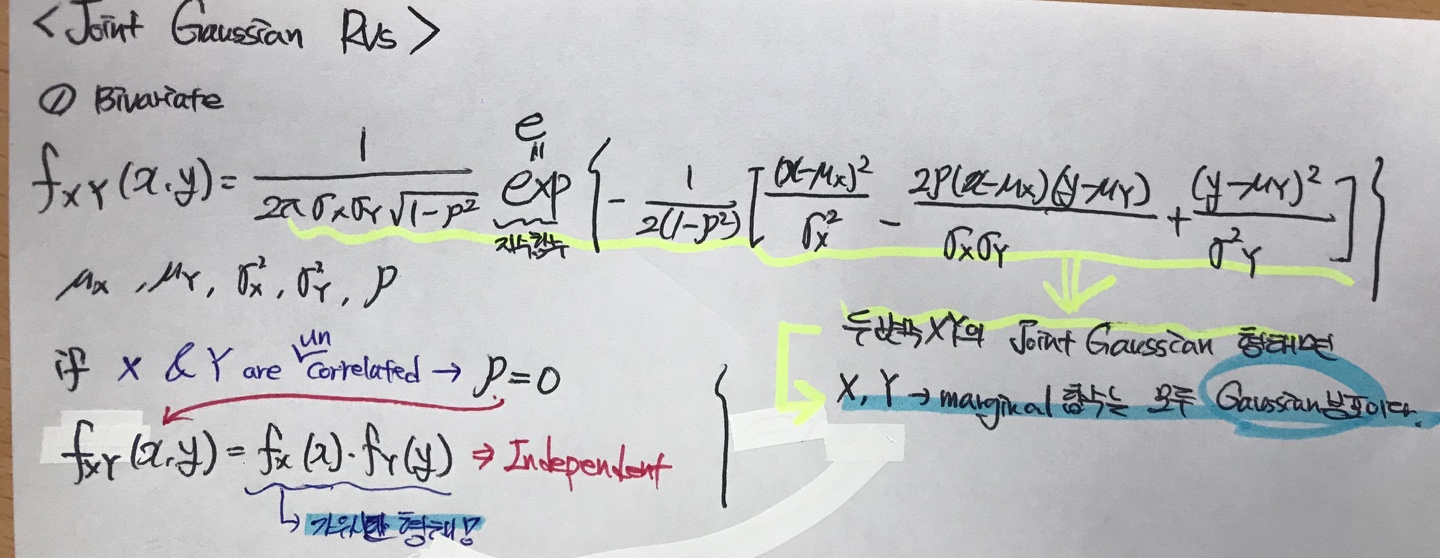
연합정규분포 이른바 Joint Gaussian Distribution이라 불리는 것에 대해서 변수가 2개일 때와 N개일 때를 알아보자.
우선 변수 2개에 대한 가우시안 분포 식은 fxy(x,y) = 이후에 있는 지수함수(exp)와 관련되어 적혀있는 식과 같다.
이 식에서 우리가 기억해야 할 건 2가지이다.
- 만약 두 확률변수 X,Y가 서로 관련성이 없다면 상관계수는 0이고 이는 결국 두 개의 확률변수 X,Y가 서로 독립적인 사건임을 의미한다
- 연합정규분포가 가우시안 분포 형태를 띄고 있다면 각 확률변수의 Marginal 함수는 모두 가우시안 분포 형태를 나타낸다.
다음은 확률변수가 N개일 때의 연합정규분포의 식에 대해 알아보자. 마찬가지로 밑에 있는 그림속의 지수함수(exp)와 관련되어 적혀있는 식과 같다. 식의 중간중간에 모르는 용어인 C(Covariance Matrix=공분산 매트릭스), 와 T=Transpose(행렬의 행과열을 바꾸는 것), X,X헤드값 = 벡터 까지 이 3가지에 대해 각각 설명을 적어놓았다.
