머신러닝에는 기본적으로 Supervised Learning(지도 학습) 과 Unsupervised Learning(비지도 학습)으로 크게 구분된다.
두개의 차이에 대해서 정의하자면, 미리 '정답'을 알려주면서 기계에게 정답을 학습시켜줌으로써 기계가 그 정답을 습득하고 스스로 알아서 정답을 판단해주는 것이 '지도학습'이다. 반면에 '정답'을 미리 알려주지 않고 패턴이 없는 비정형 데이터안에서 일정의 패턴을 찾는 것이 '비지도 학습'이라고 보면 된다.
이번 포스팅에서 작성할 머신러닝 모델은 지도학습 중에서도 가장 기본적인 모델인 Linear Regression(선형회귀분석)에 대해서 작성해보려고 한다. 우선 선형회귀분석이라 함은 연속적인 숫자값을 예측하는 것이다. 쉽게 설명하기 위해서 밑의 예시를 들어보자.

다음의 x, y 데이터는 공부시간에 따른 시험 점수이다. 첫 번째 학생은 10시간을 공부하면서 90점을 얻었고, 두번째는 9시간을 공부하면서 80점, 다음은 3시간으로 50점, 마지막은 2시간으로 30점을 얻었다. 이러한 데이터를 Train 데이터라고 부른다. 이 Train 데이터를 기계에 넣어 학습시켜서 기계는 이 데이터를 기반으로 ' 몇 시간을 공부하면 몇 점을 얻을 것이다' 라는 특정 공식(?)을 만들어내고 이에 따라 점수를 반환해준다. 예를 들어, 6시간의 공부시간을 넣으면 대략 70점(단순히 추측입니다...!)의 점수가 나올 것이다.
이제 위에서 언급했던 기계가 선정한 특정 공식이라는 것을 우리는 '가설(Hypothesis)'라고 한다. 이에 대해 이제 자세히 설명하기 위해서 더 간단한 예시를 들어보자.

위 그림은 간단한 데이터로 x=1 일 때, y=1 , x=2 일 때,y=2 , x=3일때, y=3 이라는 세가지의 데이터다. 이 데이터들을 갖고 가설을 세워보면 다음 그림과 같이 세워진다.

가설은 기본적인 식으로 H(x) = Wx + b 라는 공식으로 정의된다. 이 때 W는 가중치이며 b는 bias라는 값으로 정의 된다.
우선은 용어에 대해 생각하지는 말고 우리가 저 가설을 갖고 할 수 있는 것은 W와 b 값을 조정하면서 가장 최적의 선형을 찾아가는 것이다. ( x는 주어진 데이터가 하는 역할 이기 때문에 '우리'가 할 역할은 아니라고 해두자.)
주어진 데이터에 맞는 가장 정확한 가설을 찾는다고 하면 파란색의 선형이 될 것이다. 여기서는 주어진 데이터가 누구나 알기 쉽게 간단한 데이터지만 만약 여러가지 값의 데이터가 주어졌다고 하면 저 3가지의 가설 중에 어떤 선형이 가장 좋을지 선택하는 것에 대한 고민이 될 것이다.

어떤 선형이 가장 좋을지에 대한 기준은 바로 Cost값을 기준으로 정해진다. Cost에 대해서 알아보자.
위 그래프의 파란 선 주변에 x 표(x값 말고!!)로 되어져 있는 3가지의 값이 있다. 어떤 값은 파란선과 가까운 것도 있고,
어떤 값을 파란색과 거리가 좀 떨어져 있는 것도 있다. 이 때, 파란선과 가깝다면 Cost값이 낮아지며 Cost가 낮다는 것은 가장 적절한 선형(가장 예측을 잘하는 선형)이라고 볼 수 있다. 반면에 파란선과 멀수록 Cost값은 높아지며 Cost가 높다는 것은 가장 나쁜선형(가장 예측을 못하는 선형)이라고 볼 수 있다.

Cost 함수는 ( x표 되어진 y값{Train데이터의 값} - 파란선형의 y값{실제값} ) 과의 차이를 구해서 제곱을 한다.
여기서 제곱을 하는 이유는 실제값이 Train 데이터의 값보다 크면 음수가 되기 때문이다.
위 그림에선 3가지의 데이터가 주어 졌으니 각각 3개의 Train데이터값-y실제값의 차이를 구한 후 제곱을 해준다음
주어진 데이터의 갯수로 나누어 평균을 구해준다. 따라서 m = 데이터의 갯수이며 최종적인 수식은 그림 속 맨 밑의 수긱과 같아진다.

앞서 우리가 정의했던 가설 H(x) = Wx + b 를 cost 함수의 H(x)에다가 대입을 해보자. 그러면 위 그림의 2번째 식과 같이 W,b 값에 대한 식이 정의된다. (여기서 m= 데이터 갯수)

그렇다면 Cost를 구했는데 Cost값이 큰 값으로 나오면서 적절한 선형을 구하지 못하면 어떻게 할까...? 어떻게 하긴....
Cost를 최소화 시켜버려야 한다. Cost를 최소화시키는 알고리즘에는 여러가지가 있는데 우리는 Gradient Decent 알고리즘을 이용할 것이다. 그러면 그 전에 우리가 예시에서 사용했던 가설에 대한 Cost값을 함수로 나타내보자.
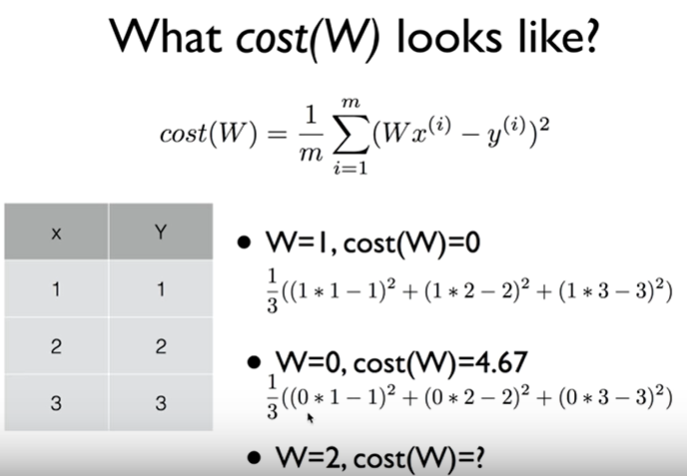
위 수식에 맞춰서 W값과 x,y값에 따라 Cost값을 구해보자. 그러면 다음과 같이 결과가 나온다.
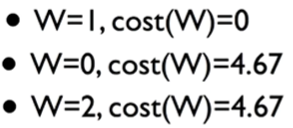
그러면 이 값에 따라 x축는 W값, y축은 Cost(W)값(=cost값)으로하고 그래프를 그려보자. 다음과 같이 나온다.


우리는 Cost값을 최소화시키기 위해서 Gradient Decent (경사도 하강) 알고리즘을 이용하는데 여기서 경사도 하강은 미분하는 것을 말한다. 고등학교 수학시간 때 배웠던 것처럼 이차함수를 미분하면 일차함수(선형함수)같이 되므로 Cost 함수의 어떤 위치에서 시작하여 미분을 계속 함으로써 가장 최소의 Cost값을 찾는 것이다. 해당 예시에서는 최소의 Cost값이 밥그릇 같은 그래프 위의 가장 일직선(평평한 점)인 W=1 일때 Cost가 0이되는 지점이다.
이러한 과정을 거치기 위해서 위의 그래프에 적혀 있는 텍스트를 읽어보자.
- 어떤 위치에서든 시작하여 계속해서 W, b값을 바꿔주며 cost를 최소화시키려고 노력하라.(해당 예시에서는 b값을 0으로 주어졌기 때문에 위에서 b값에 대한 조정이야기는 없었습니다!)
- 파라미터를 바꿀 때마다, 너는 cost값을 가능한 한 줄이기 위해서 경사도 하강(Gradient Decent)를 선택하자.
- 1,2과정을 반복해라.
- Cost값을 최소화 시킬 때까지 반복해라.
- Cost값을 최소화 시키는 점을 찾는다.

Cost(W) 함수값을 최소화 시키기 위해서는 위 그림의 두 번째 식을 적용하면 된다. 두 번째 식에서 알파값은 Cost함수(밥그릇을 엎어논 함수)에서 특정 위치에서 시작해 어느정도의 step으로 경사도를 하강해 내려올지를 결정하는 값이며 learning_rate(학습률)이라고도 부른다. 그리고 알파뒤의 값은 Cost함수를 미분해주는 식인데, 이에 대한 것은 컴퓨터가 자동으로 해주며 미분하는 과정은 다음 그림과 같다.

(여기서 갑자기 1/2m으로 바꾼 이유는 제곱을 미분할 때 2의 값이 앞으로 나오기 때문에 약분하기 쉽도록 일부러 설정해 주었다.)
추가적으로 우리가 위에서 구했던 Cost Function에 대한 함수가 Convex Function형태로 이루어져야만 Cost값을 최소화 시키기 위해(최적의 가설을 찾기 위해) Gradient Decent 알고리즘을 적용했을 때 성공적으로 Cost값을 최소화 시키는 W,b값을 찾을 수 있습니다. Convex Function형태는 다음 그림과 같다.

그림은 3차원 적이지만 위에서 보셨던 2차원 그래프(밥그릇을 엎어놓은 듯한 그래프라 언급했던 그래프)와 비슷한 형태를 하고 있다. 3차원 그래프에서도 보시다시피 W,b 값이 어느 위치에 있든 Gradient Decent알고리즘을 적용했을 때 Cost를 최소화시키는 똑같은 최적의 W,b값에 도달하는 걸 볼 수 있다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] Softmax Regression(다중분류모델) (0) | 2020.03.11 |
|---|---|
| [ML] Logistic Regression for Classification (0) | 2020.03.11 |
| [ML] 머신러닝 모델: Decision Tree(의사결정나무) (0) | 2019.11.24 |
| [용어 정리] ML/DL의 난제인 'Overfitting' 과 해결책인 'Validation' (0) | 2019.11.23 |
| [Neural Network] ANN(인공신경망) (0) | 2019.11.18 |



