이번 포스팅에서는 딥러닝 모델에서 파라미터를 초기화 하는 방법으로서 정규분포 방법, Xaiver, He 방법에 대해 알아보기로 하자. 파라미터 초기화하는 방법을 어떻게 하느냐에 따라 딥러닝 모델에서 Gradient 소실 또는 발산 문제를 발생시키는지 여부를 결정할 만큼 중요하다.

먼저 정규분포 또는 표준정규분포 방식으로 파라미터를 초기화하는 방법에 대해 알아보자.
1. 표준정규분포로 파라미터 초기화 하기
표준정규분포는 알다시피 정규분포를 평균이 0, 분산이 1인 분포로 변환하는 방법이다. 수치형 값들을 스케일링하는 방법에도 자주 활용된다. 이러한 표준정규분포 방법을 활용해 파라미터를 초기화시킬 수 있다.
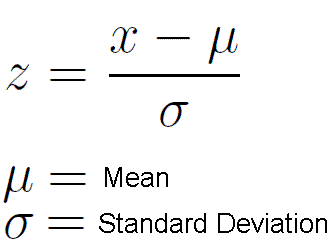
그런데 표준정규분포를 활용해 파라미터를 초기화 하면 어떻게 될까? 우선 표준정규분포로 파라미터를 초기화했다고 가정하고 Weighted Sum한 후 결과값에 sigmoid 활성함수를 적용했다 해보자. 그러면 출력값이 다음과 같이 된다.
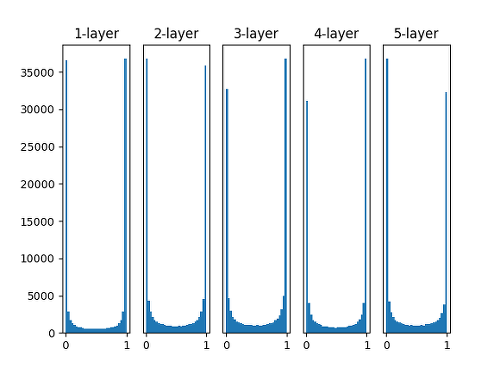
위 사진은 평균이 0, 표준편차가 1인 분포에서 파라미터를 초기화한 후 결과값에 sigmoid 활성함수를 적용한 후의 결과값 분포들이다. 그림을 잘 보면 알겠지만 모든 layer에 대해 결과값 대부분이 0 아니면 1이 되게 된다. 즉, 결과값이 대부분 0 또는 1로 수렴한다는 것인데, 이렇게 된다면 역전파 시 Graident를 계산할 때, 기울기 소실 문제가 발생할 가능성이 매우 커진다.
반면 아래와 같이 평균이 0, 표준편차가 0.01인 분포에서 파라미터를 초기화한 경우를 살펴보자.
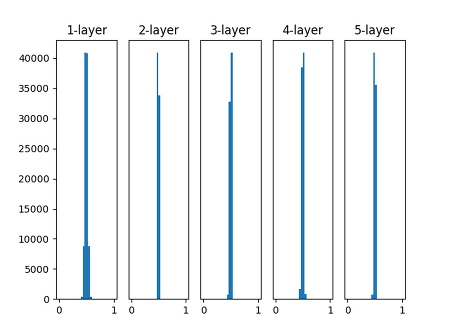
위 그래프를 보면 layer가 깊어질 수록 대부분의 출력값들이 0.5라는 한 개의 값으로 수렴하게 된다. 이렇게 모두 동일한 출력값을 갖게 되면 역전파 시 Gradient를 계산할 때 문제가 발생한다. 출력값들이 서로 달라야 Gradient를 적절하게 계산할 텐데 출력값들이 모두 동일하게 되면 Gradient를 모두 동일하게 계산할 수 밖에 없기 때문이다.
2. Xaiver Glorot 초기화 방법
이렇게 정규분포 초기화 방법의 문제점을 감안하여 Xaiver Glorot 초기화 방법이 고안되었다. Xaiver 초기화 방법은 쉽게 말해 초기화시키는 파라미터가 존재하는 Layer들의 입력/출력 노드 개수에 따라 동적으로 파라미터 값을 초기화시키는 것이다. 크게 Normal 한 방법, Uniform한 방법 2개가 존재한다. 하단의 자료를 살펴보자.

먼저 Normal 방법부터 살펴보자. Normal 방법은 초기화 시킬 파라미터 값들의 범위에서 평균은 0으로 유지하되 분산값을 위와 같이 조정하는 방법이다. 위 그림에서도 써있지만 $n_{in}$은 입력 노드의 개수, $n_{out}$은 출력 노드의 개수를 의미한다.
다음은 Uniform 방법이다. Uniform 방법은 파라미터 값들의 범위를 하한값, 상한값을 지정해서 그 범위 안에서 파라미터를 초기화 시키는 것이다. 공식은 위 자료와 같아. $n_{in}$, $n_{out}$ 수식에 대한 의미는 Normal 방법 때와 동일하다.
참고로 Tensorflow 의 Keras 모듈에서는 디폴트로 제공하는 가중치 초기화 방법은 Xaiver Uniform 방법으로 설정되어 있다고 한다.
3. He 초기화 방법
다음은 He 초기화 방법이다. He 초기화 방법은 Relu 활성함수에 보다 최적화된 파라미터 초기화 방법이다. He 초기화 방법의 공식부터 살펴보자. He 초기화 방법도 Xaiver 처럼 Normal, Uniform 방법 2가지가 존재한다.

Xavier에 비해 특이한 점은 He는 $n_{in}$ 즉, 입력 노드의 개수만 사용했다는 것이다. 나머지는 Xavier 의 공식 의미와 동일하다. Normal 방법은 분산값을, Uniform은 하한값, 상한값을 지정해 그 범위 안에서 파라미터를 초기화시킨다.
지금까지 파라미터를 초기화하는 3가지 방법에 대해 알아보았다. 이외에 파라미터 초기화 방법들이 다양하게 나와있다고 한다. 하지만 Keras와 같은 딥러닝 프레임워크에서 Xaiver 초기화 방법을 디폴트로 사용하는 만큼 위에서 소개된 파라미터 초기화 방법보다 획기적으로 성과를 이루어 낸 다른 방법은 아직 나오지 않은 듯 하다.
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] Explainable AI - Shapley Value (0) | 2021.07.25 |
|---|---|
| [ML] Unbiased boosting : CatBoost (0) | 2021.07.18 |
| [ML] 주요 인자 탐지 방법인 FDR(False Discovery Rate) (0) | 2021.03.15 |
| [ML] Partial Least Squares(부분 최소제곱법) (2) | 2021.03.14 |
| [ML] Regression metric 과 Elastic net regression (2) | 2021.01.18 |



